Zenn
📖

大規模言語モデルの圧縮技術BitNet

2024/03/02に公開
#
圧縮
#
LLM
#
大規模言語モデル
#
bitnet
tech

最近公開されたMicrosoftの研究チームによる、大規模言語モデルの計算コストを削減する研究が、その革新的な手法で業界内外から大きな注目を集めています。この研究に興味を持ち、その背後にある技術やアプローチを深く掘り下げてみることにしました。

記事:

論文:

  1. Hongyu Wang et al.: BitNet: Scaling 1-bit Transformers for Large Language Models, arXiv:2310.11453
    https://arxiv.org/abs/2310.11453
  2. Shuming Ma et al.: The Era of 1-bit LLMs: All Large Language Models are in 1.58 Bits, arXiv.2402.17764
    https://arxiv.org/abs/2402.17764

背景

大規模言語モデルの進化に伴い、その巨大なモデルサイズが新たな課題として現れています。たとえば、GPT-4では5000億から1兆のパラメータが使用され、その前のバージョンであるGPT-3.5では約3550億のパラメータが使用されていました。さらに、MetaのLLaMaモデルは70億から650億のパラメータを用いています。

これらの大規模モデルを運用するには、高性能な計算資源が必要であり、推論プロセスは時間がかかり、消費電力も増加します。これが、大規模言語モデルの適用範囲を制限する一因となっています。

このモデルサイズの問題に対処するために、モデルパラメータを圧縮してメモリ使用量と計算コストを削減しつつ、推論精度を保持する研究が進められています。

2つの研究の方向性: post-trainingとquantization-aware training

モデルパラメータの圧縮に関する研究には、主に2つのアプローチが存在します。

第一のアプローチは、学習が完了した後にパラメータを離散化して圧縮する手法です。この手法は「post-training」として知られ、そのシンプルさから実装が容易な利点があります。しかし、学習過程で圧縮を考慮していないため、推論精度の低下が懸念されます。

第二のアプローチは、学習プロセス中にパラメータを圧縮することで、圧縮された状態での学習を可能にする手法です。この手法は「quantization-aware training」と呼ばれ、post-trainingに比べて推論精度が向上することが特徴です。しかし、モデルサイズを小さくするほど、高精度を実現するためのパラメータの最適化がより困難になるという課題があります。

手法の解説

BitNetの基本的なアイデアは、TransformerのAttention機構に入力と重みを離散化するBitLinearを導入することです。TransformerのAttention機構では、入力が3つのLinear Layerを通じてそれぞれ異なる出力Q、K、Vに変換されます。一方、BitNetでは、これらのLinear Layerに代えてBitLinearを利用します。

重み行列の圧縮

BitLinear(論文[1])では、重み行列Wの各要素を、Wの全体の平均値と比較して、大きい場合は+1に、小さいまたは等しい場合は-1に変換します。具体的には、重みW \in \mathbb{R}^{n \times m}に対して、次の変換を適用します。

W' = \text{sign}(W - \alpha)

ここで、\text{sign}(x)関数は以下のように定義されます。

\text{sign}(x) = \begin{cases} +1 & \text{if } x > 0, \\ -1 & \text{if } x \leq 0, \end{cases}

そして、\alphaはWの全要素の平均値であり、

\alpha = \frac{1}{mn} \sum_{i,j} W_{ij}

により計算されます。この方法により、重みの各要素を+1と-1の二値に変換します。

入力行列の圧縮

入力行列xの各要素を[-Q_b, Q_b]（ここでQ_b = 2^{b-1}）の範囲の値に離散化します。これは、入力行列xの各値にQ_bを乗じ、xの絶対値最大値で各要素を割ることにより計算されます。

具体的には、xは以下の式で変換されます。

x' = \text{Quant}(x) = \text{Clip}\left(x \times \frac{Q_b}{\gamma}, -Q_b + \epsilon, Q_b - \epsilon\right)

ここで、

\text{Clip}(x, a, b) = \max(a, \min(b, x))

とし、

\gamma = \|x\|_{\infty}

\epsilonは、計算のオーバーフローを避けるための小さい値です。ReLUなどの活性化関数の代わりに、xの各要素からxのすべての要素の最小値を引くことにより値を[0,Q_b]の範囲の値に変換します。x’ = \text{Quant}(x) = \text{Clip}((x - \gamma)) \times \frac{Q_b}{\gamma}, \epsilon, Q_b - \epsilon)ここで、

\gamma = \min_{ij}x_{ij}

上記の計算により得られたW’とx’を用いて、y=W’x’により行列計算は行われます。

論文[2]では、Wを\{-1,+1\}の二値の代わりに、\{-1,0,+1\}の三値に変換することで、より高い精度達成できることが報告されています。

結果

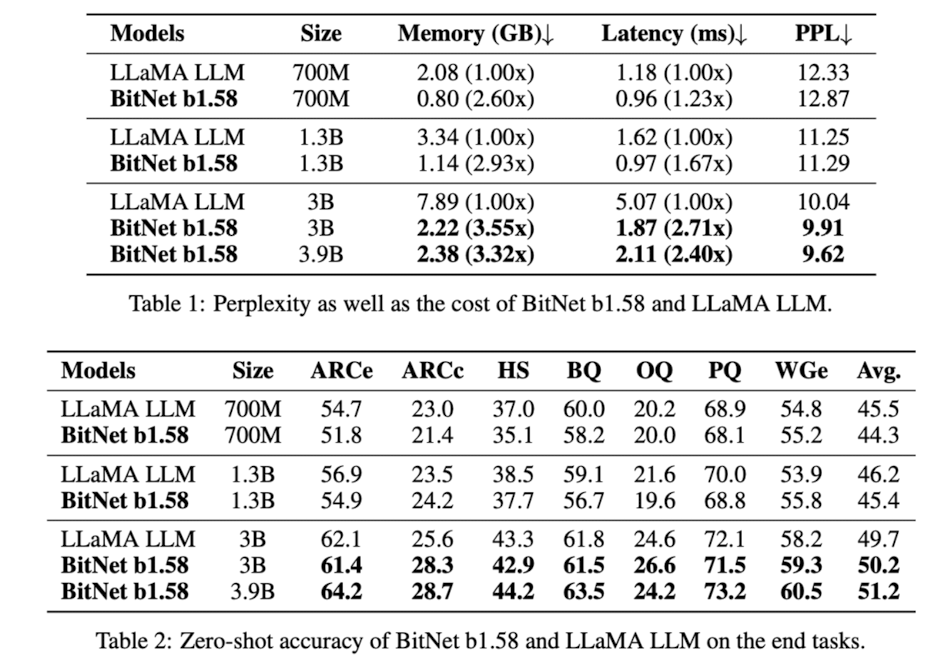
LLaMAとの精度比較では、ほとんどのデータセット上でLLaMAと同等かそれをわずかに上回る精度を達成しており、メモリ効率やレイテンシーの面では顕著な有効性を示しています。

Discussion