【Python】実践データ分析100本ノック 第7章
この記事は、現場で即戦力として活躍することを目指して作られた現場のデータ分析の実践書である「Python 実践データ分析 100本ノック(秀和システム社)」で学んだことをまとめています。
ただし、本を参考にして自分なりに構成などを変更している部分が多々あるため、ご注意ください。細かい解説などは是非本をお手に取って読まれてください。

【リンク紹介】
・【一覧】Python実践データ分析100本ノック
・これまで書いたシリーズ記事一覧
目的
最適化計算を行ういくつかのライブラリを用いて、最適化計算を実際に行っていく
Import
# 必要に応じてインストールを行う
#!pip install pulp > /dev/null # 最適化モデルの作成を行う
#!pip install ortoolpy > /dev/null # 目的関数を生成して解く
%%time
import numpy as np
import pandas as pd
from gc import collect # ガーベッジコレクション
from colorama import Fore, Style, init # Pythonの文字色指定ライブラリ
from IPython.display import display_html, clear_output
import matplotlib.pyplot as plt
%matplotlib inline
import networkx as nx
from itertools import product
from pulp import LpVariable, lpSum, value
from ortoolpy import model_min, model_max, addvars, addvals
%%time
# テキスト出力の設定
def PrintColor(text:str, color = Fore.GREEN, style = Style.BRIGHT):
print(style + color + text + Style.RESET_ALL);
# displayの表示設定
pd.set_option('display.max_columns', 50);
pd.set_option('display.max_rows', 50);
print()
collect()
Knock61:最適輸送ルートをネットワークで確認する
【Python】実践データ分析100本ノック 第6章で取り組んだ輸送最適化問題を、最適化計算ライブラリpulpとortoolpyを用いて解いていきます。
[参考資料]
%%time
"""データ読み込み"""
df_tc = pd.read_csv('trans_cost.csv', # 倉庫と工場間の輸送コスト
index_col = '工場'
)
df_demand = pd.read_csv('demand.csv') # 工場の製品生産量に対する需要
df_supply = pd.read_csv('supply.csv') # 倉庫が供給可能な部品数の上限
print()
collect()
%%time
"""読み込んだデータを確認"""
PrintColor(f'\n df_tc:倉庫と工場間の輸送コスト')
display(df_tc)
PrintColor(f'\n df_demand:工場の製品生産量に対する需要')
display(df_demand)
PrintColor(f'\n df_supply:倉庫が供給可能な部品数の上限')
display(df_supply)
print()
collect()
%%time
"""初期設定"""
np.random.seed(1)
nw = len(df_tc.index) # 行数
nf = len(df_tc.columns) # 列数
pr = list(product(range(nw), range(nf))) # 行数と列数を組み合わせたデカルト積を作成する。例:(0, 3)など
"""数理モデル作成"""
m1 = model_min() # 最小化を行うモデルをインスタンス化
# 変数オブジェクトの作成。最小値制約を0と定める。
v1 = {(i, j):LpVariable('v%d_%d'%(i, j), lowBound = 0) for i, j in pr}
# 目的関数の設定。数理モデルに足すように代入することで設定可能
m1 += lpSum(df_tc.iloc[i][j] * v1[i, j] for i, j in pr)
# 制約条件の設定
for i in range(nw):
m1 += lpSum(v1[i, j] for j in range(nf)) <= df_supply.iloc[0][i]
for j in range(nf):
m1 += lpSum(v1[i, j] for i in range(nw)) >= df_demand.iloc[0][j]
# 実行して問題を解く
m1.solve()
"""総輸送コスト計算"""
df_tr_sol = df_tc.copy()
total_cost = 0
for k, x in v1.items():
i, j = k[0], k[1]
df_tr_sol.iloc[i][j] = value(x)
total_cost += df_tc.iloc[i][j] * value(x)
print()
collect()
%%time
PrintColor(f'\n 最適化計算による輸送コスト')
display(df_tr_sol)
PrintColor('最適化計算による総輸送コスト(万円):' + str(total_cost))
print()
collect()
Knock62:最適輸送ルートをネットワークで確認する
計算されたコストをもとに、Knock57と同じようにしてネットワーク可視化を行います。
%%time
"""データ読み込み"""
df_tr = df_tr_sol.copy() # 最適化計算による輸送コスト
df_pos = pd.read_csv('trans_route_pos.csv') # 倉庫・工場の位置情報
print()
collect()
%%time
"""読み込んだデータを確認"""
PrintColor(f'\n df_tr:最適化計算による輸送コスト')
display(df_tr)
PrintColor(f'\n df_pos:倉庫・工場の位置情報')
display(df_pos)
print()
collect()
%%time
"""グラフオブジェクトの作成"""
G = nx.Graph()
# 頂点の設定
for i in range(len(df_pos.columns)):
G.add_node(df_pos.columns[i])
# 辺の設定とエッジの重みのリスト化
num_pre = 0
edge_weights = []
size = 0.1
for i in range(len(df_pos.columns)):
for j in range(len(df_pos.columns)):
if not (i == j):
# 辺の追加
G.add_edge(df_pos.columns[i], df_pos.columns[j])
# エッジの重みの追加
if num_pre < len(G.edges):
num_pre = len(G.edges)
weight = 0
if (df_pos.columns[i] in df_tr.columns) and (df_pos.columns[j] in df_tr.index):
if df_tr[df_pos.columns[i]][df_pos.columns[j]]:
weight = df_tr[df_pos.columns[i]][df_pos.columns[j]] * size
elif (df_pos.columns[j] in df_tr.columns) and (df_pos.columns[i] in df_tr.index):
if df_tr[df_pos.columns[j]][df_pos.columns[i]]:
weight = df_tr[df_pos.columns[j]][df_pos.columns[i]] * size
edge_weights.append(weight)
# 座標の設定
pos = {}
for i in range(len(df_pos.columns)):
node = df_pos.columns[i]
pos[node] = (df_pos[node][0], df_pos[node][1])
# 描画
nx.draw(G, pos,
with_labels = True,
font_size = 16,
node_size = 1000,
node_color = 'k',
font_color = 'w',
width = edge_weights
)
# 画像を保存
plt.savefig('Knock62.png')
# 表示
plt.show()
print()
collect()
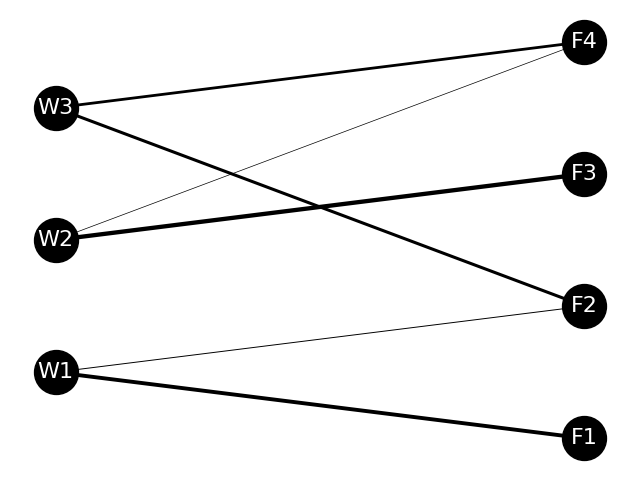
Knock63:最適輸送ルートが制約条件内に収まっているかを確認する
Knock60で作成した制約条件を計算する関数を用いて、最適計算を行った結果の輸送ルートが制約条件に収まっているかを確認します。
%%time
"""データ読み込み"""
df_demand = pd.read_csv('demand.csv') # 工場の製品生産量に対する需要
df_supply = pd.read_csv('supply.csv') # 倉庫が供給可能な部品数の上限
print()
collect()
%%time
"""読み込んだデータを確認"""
PrintColor(f'\n df_demannd:工場の製品生産量に対する需要')
display(df_demand)
PrintColor(f'\n df_supply:倉庫が供給可能な部品数の上限')
display(df_supply)
print()
collect()
%%time
"""制約条件計算関数"""
# 需要側
def condition_demand(df_tr, df_demand):
flag = np.zeros(len(df_demand.columns))
for i in range(len(df_demand.columns)):
temp_sum = sum(df_tr[df_demand.columns[i]])
if (temp_sum >= df_demand.iloc[0][i]):
flag[i] = 1
return flag
# 供給側
def condition_supply(df_tr, df_supply):
flag = np.zeros(len(df_supply.columns))
for i in range(len(df_supply.columns)):
temp_sum = sum(df_tr.loc[df_supply.columns[i]])
if temp_sum <= df_supply.iloc[0][i]:
flag[i] = 1
return flag
print()
collect()
%%time
PrintColor('需要条件計算結果:' + str(condition_demand(df_tr_sol, df_demand)))
PrintColor('供給条件計算結果:' + str(condition_supply(df_tr_sol, df_supply)))
print()
collect()
Knock64:生産計画に関するデータを読み込む
次に、どの製品をどれだけ作るか(生産計画)に取り組みます。
%%time
"""データ読み込み"""
df_material = pd.read_csv('product_plan_material.csv', index_col = '製品')
df_profit = pd.read_csv('product_plan_profit.csv', index_col = '製品')
df_stock = pd.read_csv('product_plan_stock.csv', index_col = '項目')
df_plan = pd.read_csv('product_plan.csv', index_col = '製品')
print()
collect()
%%time
"""読み込んだデータを確認"""
PrintColor(f'\n df_material:製品の製造に必要な原料の割合')
display(df_material)
PrintColor(f'\n df_profit:製品の利益')
display(df_profit)
PrintColor(f'\n df_stock:原料の在庫')
display(df_stock)
PrintColor(f'\n df_plan:製品の生産量')
display(df_plan)
print()
collect()
Knock65:利益を計算する関数を作る
まずは利益を計算する関数を作り、これを目的関数として最大化することを検討します。
%%time
"""利益計算関数"""
def product_plan(df_profit, df_plan):
profit = 0
for i in range(len(df_profit.index)):
for j in range(len(df_plan.columns)):
profit += df_profit.iloc[i][j] * df_plan.iloc[i][j] # 各製品の利益と製造量の積を足す
return profit
PrintColor('総利益(万円):' + str(product_plan(df_profit, df_plan)))
print()
collect()
Knock66:生産最適化問題を解く
定式化した目的関数である利益関数を最大化するために、最適化計算を行います。
%%time
df = df_material.copy()
inv = df_stock
"""数理モデル作成"""
m = model_max()
# 変数オブジェクトの作成
v1 = {(i):LpVariable('v%d'%(i), lowBound = 0) for i in range(len(df_profit))}
# 目的関数の設定
m += lpSum(df_profit.iloc[i] * v1[i] for i in range(len(df_profit)))
# 制約条件の設定
for i in range(len(df_material.columns)):
m += lpSum(df_material.iloc[j, i] * v1[j] for j in range(len(df_profit))) <= df_stock.iloc[:, i]
# 実行して問題を解く
m.solve()
"""総利益を計算"""
df_plan_sol = df_plan.copy()
for k, x in v1.items():
df_plan_sol.iloc[k] = value(x)
print()
collect()
%%time
PrintColor(f'\n df_plan_sol')
display(df_plan_sol)
PrintColor('総利益(万円):' + str(value(m.objective)))
print()
collect()
Knock67:最適生産計画が制約条件内に収まっているかどうかを確認する
%%time
"""制約条件計算関数"""
def condition_stock(df_plan, df_material, df_stock):
flag = np.zeros(len(df_material.columns))
for i in range(len(df_material.columns)):
temp_sum = 0
for j in range(len(df_material.index)):
temp_sum = temp_sum + df_material.iloc[j][i] * float(df_plan.iloc[j])
if (temp_sum <= float(df_stock.iloc[0][i])):
flag[i] = 1
print(df_material.columns[i] + ' 使用料:' + str(temp_sum) + ', 在庫:' + str(float(df_stock.iloc[0][i])))
return flag
PrintColor('制約条件計算結果:' + str(condition_stock(df_plan_sol, df_material, df_stock)))
print()
collect()
Knock68:物流ネットワーク設計問題を解く
これまで輸送ルートと生産計画の最適化問題をそれぞれ個別で考えましたが、実際の物流ネットワークは同時に考える必要があります。
%%time
製品 = list('AB')
需要地 = list('PQ')
工場 = list('XY')
レーン = (2, 2)
# 輸送費表
tbdi = pd.DataFrame(((j, k) for j in 需要地 for k in 工場), columns = ['需要地', '工場'])
tbdi['輸送費'] = [1, 2, 3, 1]
PrintColor(f'\n tbdi:輸送費表')
display(tbdi)
# 需要表
tbde = pd.DataFrame(((j, i) for j in 需要地 for i in 製品), columns = ['需要地', '製品'])
tbde['需要'] = [10, 10, 20, 20]
PrintColor(f'\n tbde:需要表')
display(tbde)
# 生産表
tbfa = pd.DataFrame(((k, l, i, 0, np.inf) for k ,nl in zip (工場, レーン) for l in range(nl) for i in 製品),
columns = ['工場', 'レーン', '製品', '下限', '上限'])
tbfa['生産費'] = [1, np.nan, np.nan, 1, 3, np.nan, 5, 3]
tbfa.dropna(inplace = True)
tbfa.loc[4, '上限'] = 10
PrintColor(f'\n tbfa:生産表')
display(tbfa)
print()
collect()
%%time
from ortoolpy import logistics_network
_, tbdi2, _ = logistics_network(tbde, tbdi, tbfa)
PrintColor(f'\n tbfa:生産表(ValY = 最適生産量)')
display(tbfa)
PrintColor(f'\n tbdi2:輸送費表(ValX = 最適輸送量)')
display(tbdi2)
print()
collect()
Knock69:ネットワークにおける輸送コストとその内訳を計算する
%%time
trans_cost = 0
for i in range(len(tbdi2.index)):
trans_cost += tbdi2['輸送費'].iloc[i] * tbdi2['ValX'].iloc[i]
PrintColor('総輸送コスト(万円):' + str(trans_cost))
print()
collect()
Knock70:最適ネットワークにおける生産コストとその内訳を計算する
%%time
product_cost = 0
for i in range(len(tbfa.index)):
product_cost += tbfa['生産費'].iloc[i] * tbfa['ValY'].iloc[i]
PrintColor('総生産コスト(万円):' + str(product_cost))
print()
collect()
ortoolpyを用いずに解く
なお、このortoolpyライブラリは一般的なライブラリではなく、かつどのように処理されているのかがわかりにくい側面があります。そこでortoolpyを用いずに解く方法がpiz3inさんの記事「「Python実践データ分析100本ノック」実践編②最適化問題をortoolpyを用いずに解く」に書れていますので、気になる方は是非読まれてください。
ご協力のほどよろしくお願いします。
Discussion