【Python】実践データ分析100本ノック 第8章
この記事は、現場で即戦力として活躍することを目指して作られた現場のデータ分析の実践書である「Python 実践データ分析 100本ノック(秀和システム社)」で学んだことをまとめています。
ただし、本を参考にして自分なりに構成などを変更している部分が多々あるため、ご注意ください。細かい解説などは是非本をお手に取って読まれてください。

【リンク紹介】
・【一覧】Python実践データ分析100本ノック
・これまで書いたシリーズ記事一覧
目的
数値シミュレーションで消費者行動を予測する
Import
%%time
import numpy as np
import pandas as pd
from gc import collect # ガーベッジコレクション
from colorama import Fore, Style, init # Pythonの文字色指定ライブラリ
from IPython.display import display_html, clear_output
import matplotlib.pyplot as plt
%matplotlib inline
import networkx as nx
%%time
# テキスト出力の設定
def PrintColor(text:str, color = Fore.GREEN, style = Style.BRIGHT):
print(style + color + text + Style.RESET_ALL);
# displayの表示設定
pd.set_option('display.max_columns', 50);
pd.set_option('display.max_rows', 50);
print()
collect()
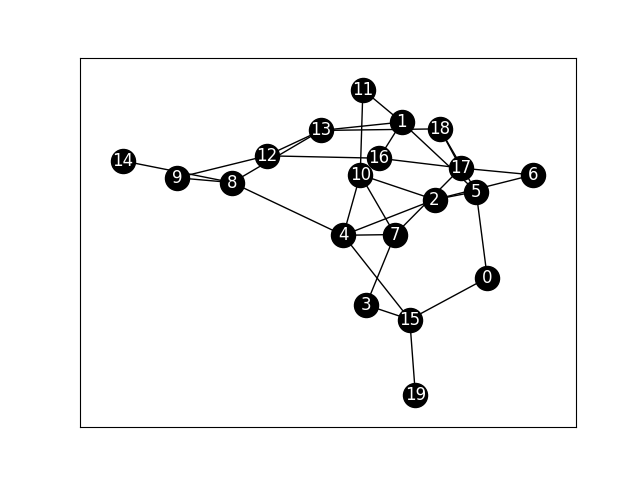
Knock71:人間関係のネットワークを可視化する
消費者の口コミによる行動分析を行うために、リピーター20人のつながりデータを分析します。
%%time
"""データ読み込み"""
df_links = pd.read_csv('links.csv', index_col = 'Node')
"""読み込んだデータを確認"""
PrintColor(f'\n df_lilnks:リピーター20人のSNSでのつながり(つながり有り=1, つながり無し=0)')
display(df_links.head())
print()
collect()
リピーターのネットワークを可視化します。可視化の方法は【Python】実践データ分析100本ノック 第6章を参考にしてください。
%%time
"""グラフオブジェクトの作成"""
G = nx.Graph()
# 行数を格納
NUM = len(df_links.index)
# 頂点の設定
for i in range(NUM):
node_no = df_links.columns[i].strip('Node') # カラム名の'Node'を削除して、数字のみを格納する
G.add_node(str(node_no)) # 頂点の作成
# 辺の設定
for i in range(NUM): # 行ごとにループ
for j in range(NUM): # 列ごとにループ※実際にiが行、jが列と判別できないが行列の定義に準じた
node_name = 'Node' + str(j)
if df_links[node_name].iloc[i] == 1: # j列のi行目に1が格納されていれば
G.add_edge(str(i), str(j)) # 辺を作成
# 描画 ※draw_networkx()関数はdraw()関数とは違いリンクの多いものが中心に集まる
nx.draw_networkx(G,
node_color = 'k',
edge_color = 'k',
font_color = 'w'
)
# グラフを保存
plt.savefig('Knock71.png')
plt.show()
print()
collect()
Knock72:口コミによる情報伝播の様子を可視化する
「10のつながりのうち、10%の確率で口コミが伝播していく」と仮定し、口コミの伝播の様子をシミュレーションします。
%%time
"""
パラメータ
----------------------------------------------------
percent : float.口コミが伝播する確率
----------------------------------------------------
"""
"""口コミを伝播させるかどうかを決定する関数"""
def determine_link(percent):
rand_val = np.random.rand()
if rand_val <= percent:
return 1
else:
return 0
print()
collect()
%%time
"""
パラメータ
----------------------------------------------------
num : int.リピーター数
list_active : リスト.それぞれのノード(人)に口コミが伝わったかを1,0で表現
percent_percolation : float.伝播する確率
----------------------------------------------------
"""
"""口コミをシミュレートする"""
def simulate_percolation(num, list_active, percent_percolation):
for i in range(num):
# iにもし口コミが伝わったら
if list_active[i] == 1:
for j in range(num):
node_name = 'Node' + str(j)
j_links_i = df_links[node_name].iloc[i] # 次のif文用に要約変数を作成
percolate = determine_link(percent_percolation) # 次のif文用に要約変数を作成
# jがiとつながっていて、かつ口コミが伝播されたら
if (j_links_i == 1) & (percolate == 1) :
# jにも口コミが伝わる
list_active[j] = 1
return list_active
print()
collect()
[テキストとの変更点]
テキストでsimulate_percolation()関数のjループ部分は、以下のように記述されていました。
def simulate_percolation(num, list_active, percent_percolation):
for i in range(num):
# iにもし口コミが伝わったら
if list_active[i] == 1:
for j in range(num):
node_name = 'Node' + str(j)
if df_links[node_name].iloc[i] == 1:
if determine_link(percent_percolation) == 1:
list_active[j] = 1
return list_active
このコード記述には以下の問題点があると考えます。
- if文の条件文が長くなってしまい、理解しづらい
- ネストが深く、コードが理解しにくい
この問題に対して、以下のように改善しました。
- if文で使う前に要約変数を作成し、目的を明らかにする
- 後半のif文が2回連続で用いられている部分に注目し、論理変換でif文1回の使用に変更する
特に2.については、次のように行いました。まず、それぞれのif文の条件をA, Bに置き換え、処理list_active[j] = 1をCに置き換えます。つまり
def simulate_percolation(num, list_active, percent_percolation):
for i in range(num):
# iにもし口コミが伝わったら
if list_active[i] == 1:
for j in range(num):
node_name = 'Node' + str(j)
if A:
if B:
C
return list_active
となります。この2重のifは、論理構造として以下のようになっています。
ここで、命題「□ ならば ●」は命題「□でない または ●」と同値であることを利用して、同値変形を行います。
よって、この同値変形から次のようにコードを改良できることがわかります。
def simulate_percolation(num, list_active, percent_percolation):
for i in range(num):
# iにもし口コミが伝わったら
if list_active[i] == 1:
for j in range(num):
node_name = 'Node' + str(j)
if A & B:
C
return list_active
これに、1.で提案した要約変数を組み合わせて改善したコードが、上記のものとなります。
なお、この改善は
「リーダブルコード ―より良いコードを書くためのシンプルで実践的なテクニック (Theory in practice)」
を参考に行いました。興味のある方は是非お手に取ってみてください。
%%time
"""シミュレート実行"""
percent_percolation = 0.1 # 伝播確率を10%とする
T_NUM = 36 # ステップ回数(36か月繰り返すという意味)
NUM = len(df_links.index) # リピーター数を格納
list_active = np.zeros(NUM) # 初期値としてすべて0を格納する
list_active[0] = 1
# 伝播結果を格納するリストを作成。各ステップ回数ごとにまとめて格納される
list_timeSeries = []
for t in range(T_NUM):
# シミュレート実行
list_active = simulate_percolation(NUM,
list_active,
percent_percolation
)
# シミュレーション結果を格納する
list_timeSeries.append(list_active.copy())
print()
collect()
%%time
"""伝播した様子を表したネットワークを可視化"""
def active_node_coloring(list_active):
# 色指定用のリストを準備。伝播したリピーターには赤色を指定する
list_color = []
rc_num = len(list_timeSeries[t]) # rc:repeat customer
for i in range(rc_num):
if list_timeSeries[t][i] == 1:
list_color.append('r')
else:
list_color.append('k')
return list_color
print()
collect()
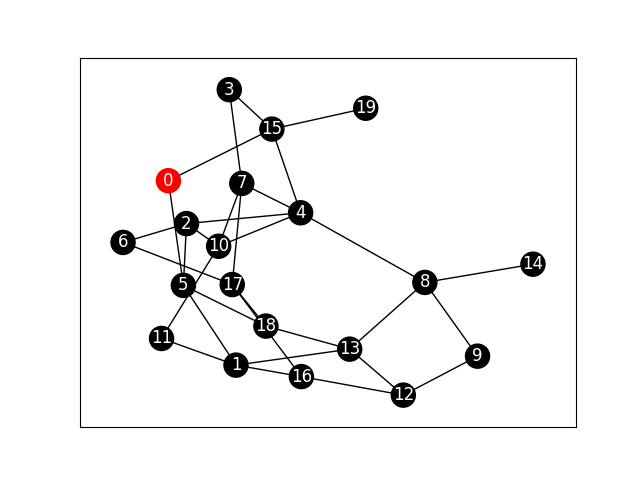
%%time
"""ステップ回数0回目の時のネットワークを可視化"""
t = 0
nx.draw_networkx(G,
font_color = 'w',
node_color = active_node_coloring(list_timeSeries[t]))
# グラフを保存
plt.savefig('Knock72_1.png')
plt.show()
print()
collect()
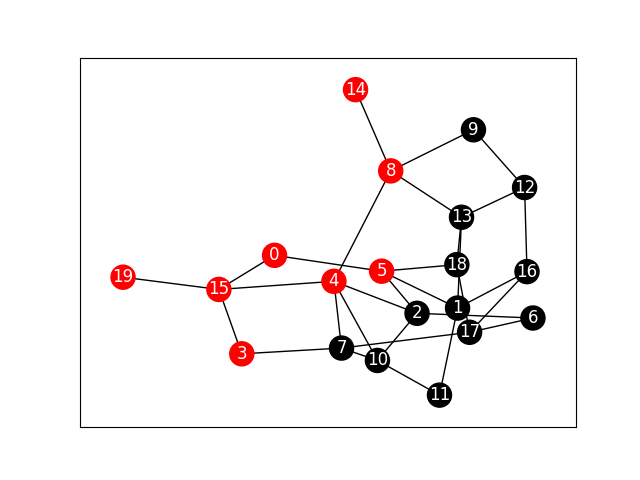
%%time
"""ステップ回数11回目の時のネットワークを可視化"""
t = 11
nx.draw_networkx(G,
font_color = 'w',
node_color = active_node_coloring(list_timeSeries[t]))
# グラフを保存
plt.savefig('Knock72_2.png')
plt.show()
print()
collect()
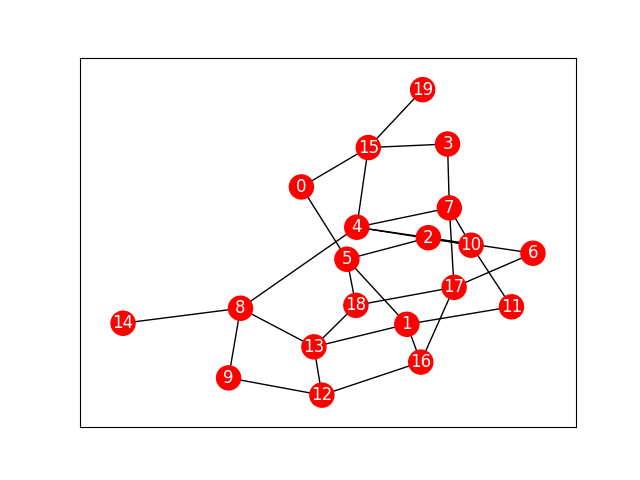
%%time
"""ステップ回数35回目の時のネットワークを可視化"""
t = 35
nx.draw_networkx(G,
font_color = 'w',
node_color = active_node_coloring(list_timeSeries[t]))
# グラフを保存
plt.savefig('Knock72_3.png')
plt.show()
print()
collect()
Knock73:口コミ数の時系列変化をグラフ化する
口コミされた数を時系列でグラフ化していきます。
%%time
# 各ステップごとの伝播数を格納するためのリストを作成
list_timeSeries_num = []
for i in range(len(list_timeSeries)):
list_timeSeries_num.append(sum(list_timeSeries[i]))
plt.plot(list_timeSeries_num)
# グラフを保存
plt.savefig('Knock73.png')
plt.show()
print()
collect()
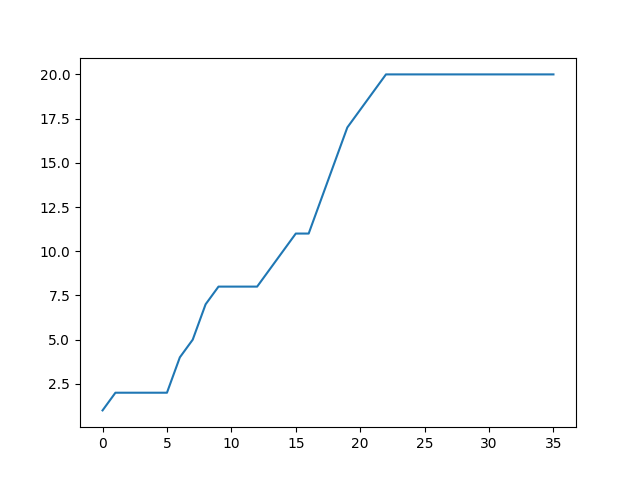
Knock74:会員数の時系列変化をシミュレーションする
これまでの手法を用いて、今度は口コミによりスポーツジムの利用状況がどのように変化敷いていくのかをシミュレーションします。
%%time
"""
パラメータ
----------------------------------------------------
num : int.リピーター数
list_active : リスト.それぞれのノード(人)に口コミが伝わったかを1,0で表現
percent_percolation : float.伝播する確率
percent_disapparence : float.突然利用しなくなる確率(消失確率)
df_links : 読み込むデータ
----------------------------------------------------
"""
def simulate_population(num, list_active, percent_percolation, percent_disapparence, df_links):
# 拡散
for i in range(num):
if list_active[i] == 1:
for j in range(num):
node_name = 'Node' + str(j)
j_links_i = df_links[node_name].iloc[i]
percolate = determine_link(percent_percolation)
if (j_links_i == 1) & (percolate == 1):
list_active[j] = 1
# 消滅
for i in range(num):
disappear = determine_link(percent_disapparence)
if disappear == 1:
list_active[i] = 0
return list_active
print()
collect()
%%time
"""シミュレーションの実行"""
percent_percolation = 0.1 # 伝播確率を10%とする
percent_disapparence = 0.05 # 消失確率を5%とする
T_NUM = 100 # ステップ回数(100ヶ月繰り返すという意味)
NUM = len(df_links.index) # リピーター数を格納
list_active = np.zeros(NUM) # 初期値としてすべて0を格納
list_active[0] = 1
# 伝播結果を格納するリストを作成。各ステップ回数ごとにまとめて格納される
list_timeSeriex = []
for t in range(T_NUM):
# シミュレート実行
list_active = simulate_population(NUM,
list_active,
percent_percolation,
percent_disapparence,
df_links
)
# シミュレーション結果を格納する
list_timeSeries.append(list_active.copy())
print()
collect()
%%time
"""会員数の時系列変化をグラフ化する"""
list_timeSeries_num = []
for i in range(len(list_timeSeries)):
list_timeSeries_num.append(sum(list_timeSeries[i]))
# グラフを保存
plt.savefig('Knock74_1.png')
plt.plot(list_timeSeries_num)
print()
collect()
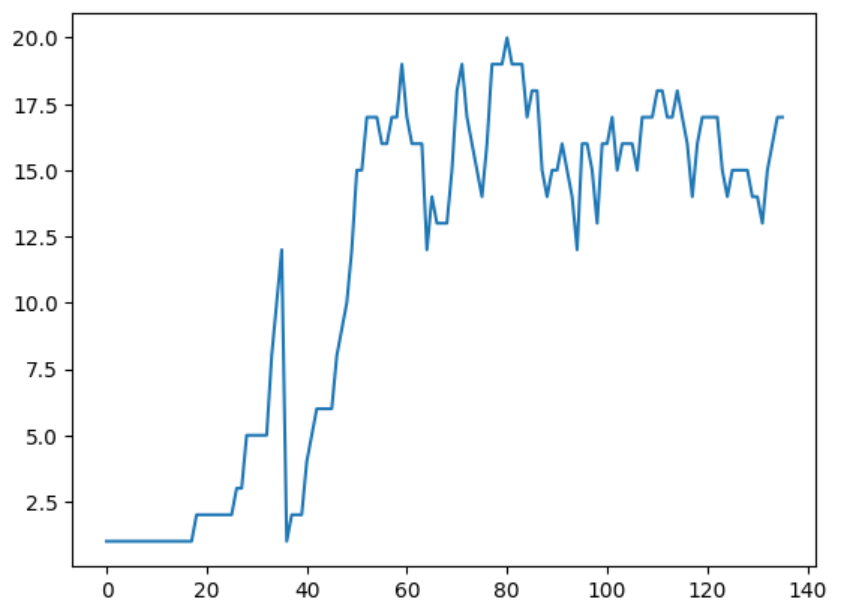
次に消滅確率を5%から**20%**に変えてシミュレーションを行い、会員数の時系列変化を見ていきます。
%%time
"""シミュレーション実行"""
percent_disapparence = 0.2 # 消滅確率を20%とする
list_active = np.zeros(NUM) # リピーター数を格納
list_active[0] = 1
list_timeSeries = [] # 伝播結果を格納するリストを作成
for t in range(T_NUM):
# シミュレート実行
list_active = simulate_population(NUM,
list_active,
percent_percolation,
percent_disapparence,
df_links
)
# シミュレーション結果を格納する
list_timeSeries.append(list_active.copy())
print()
collect()
%%time
"""会員数の時系列変化をグラフ化する"""
list_timeSeries_num = []
for i in range(len(list_timeSeries)):
list_timeSeries_num.append(sum(list_timeSeries[i]))
plt.plot(list_timeSeries_num)
# グラフを保存
plt.savefig('Knock74_2.png')
plt.show()
print()
collect()
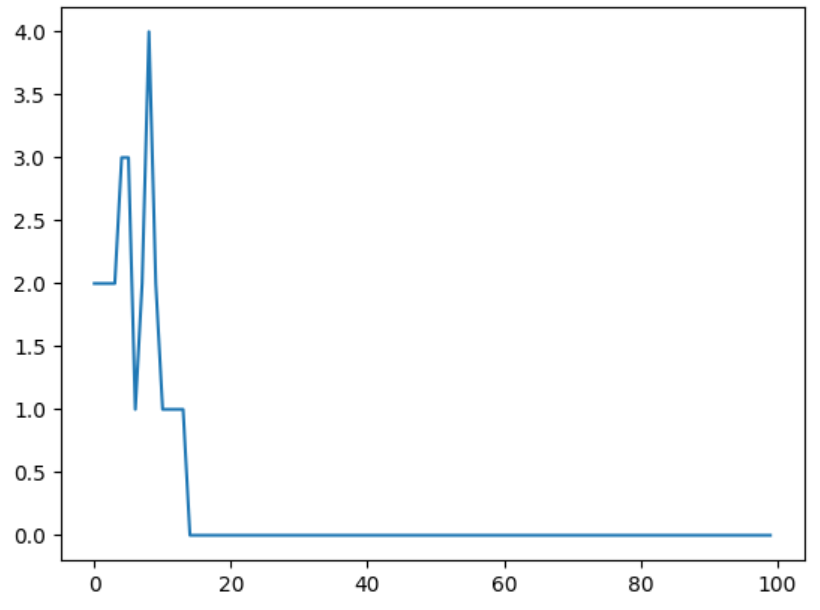
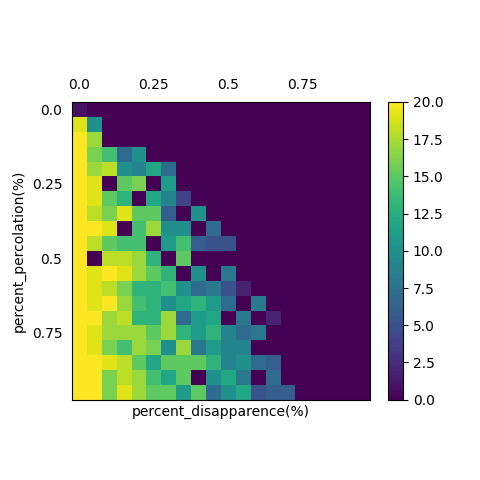
Knock75:パラメータの全体像を、「相図」を見ながら把握する
%%time
print('相図計算開始')
T_NUM = 100 # ステップ回数
NUM_PhaseDiagram = 20
phaseDiagram = np.zeros((NUM_PhaseDiagram, NUM_PhaseDiagram))
for i_p in range(NUM_PhaseDiagram):
for i_d in range(NUM_PhaseDiagram):
percent_percolation = 0.05 * i_p # 伝播確率5%から始まり、5%ずつ確率を上げていく
percent_disapparence = 0.05 * i_d # 証明確率5%から始まり、5%ずつ確率を上げていく
list_active = np.zeros(NUM)
list_active[0] = 1
for t in range(T_NUM):
# シミュレーションを実行
list_active = simulate_population(NUM,
list_active,
percent_percolation,
percent_disapparence,
df_links)
#シミュレーション結果を格納
phaseDiagram[i_p][i_d] = sum(list_active)
# 格納されたデータを確認
print(phaseDiagram)
print()
collect()
%%time
"""相図を描画"""
plt.matshow(phaseDiagram)
plt.colorbar(shrink = 0.8)
plt.xlabel('percent_disapparence(%)')
plt.ylabel('percent_percolation(%)')
plt.xticks(np.arange(0.0, 20.0, 5), np.arange(0.0, 1.0, 0.25))
plt.yticks(np.arange(0.0, 20.0, 5), np.arange(0.0, 1.0, 0.25))
plt.tick_params(bottom = False,
left = False,
right = False,
top = False
)
# グラフを保存
plt.savefig('Knock75.png')
plt.show()
print()
collect()
Knock76:実データを読み込む
ここからスポーツジムの会員全体の実データを用いたシミュレーションを行います。まずは会員540人のデータが格納されたファイルを読み込みます。
%%time
"""データ読み込み"""
df_mem_links = pd.read_csv('links_members.csv', # リピーター540人のSNSでのつながり
index_col = 'Node'
)
df_mem_info = pd.read_csv('info_members.csv', # リピーター540人の月々の利用状況
index_col = 'Node'
)
"""読み込んだデータを確認"""
display(df_mem_links.head())
print()
collect()
Knock77:リンク数の分布を可視化する
%%time
NUM = len(df_mem_links.index)
array_linkNum = np.zeros(NUM)
for i in range(NUM):
array_linkNum[i] = sum(df_mem_links['Node' + str(i)])
print()
collect()
%%time
plt.hist(array_linkNum, bins = 10, range = (0, 250))
# グラフを保存
plt.savefig('Knock77.png')
plt.show()
print()
collect()

Knock78:シミュレーションのために実データからパラメータを推定する
%%time
NUM = len(df_mem_info.index)
T_NUM = len(df_mem_info.columns) - 1
"""消滅の確率推定"""
count_active = 0
count_active_to_inactive = 0
for t in range(T_NUM):
for i in range(NUM):
if (df_mem_info.iloc[i][t] == 1):
count_active_to_inactive += 1
if (df_mem_info.iloc[i][t + 1] == 0):
count_active += 1
estimated_percent_disapparence = count_active / count_active_to_inactive
print()
collect()
%%time
"""拡散の確率推定"""
count_link = 0
count_link_to_active = 0
count_link_temp = 0
for t in range(T_NUM):
df_link_t = df_mem_info[df_mem_info[str(t)] == 1]
temp_flag_count = np.zeros(NUM)
for i in range(len(df_link_t.index)):
index_i = int(df_link_t.index[i].replace('Node', ''))
df_link_temp = df_mem_links[df_mem_links['Node' + str(index_i)] == 1]
for j in range(len(df_link_temp.index)):
index_j = int(df_link_temp.index[j].replace('Node', ''))
if (df_mem_info.iloc[index_j][t] == 0):
if (temp_flag_count[index_j] == 0):
count_link += 1
if (df_mem_info.iloc[index_j][t + 1] == 1):
if (temp_flag_count[index_j] == 0):
temp_flag_count[index_j] = 1
count_link_to_active += 1
estimated_percent_percolation = count_link_to_active / count_link
print()
collect()
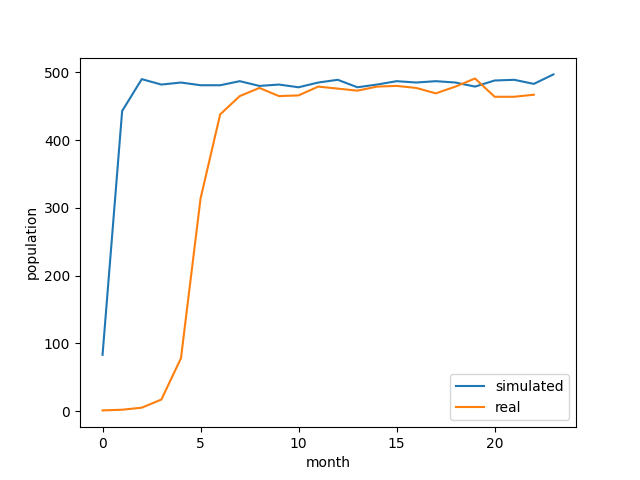
Knock79:実データとシミュレーションを比較する
%%time
"""シミュレーション実行"""
percent_percolation = 0.039006364196263604
percent_disapparence = 0.10147163541419416
T_NUM = 24
NUM = len(df_mem_links.index)
list_active = np.zeros(NUM)
list_active[0] = 1
list_timeSeries = []
for t in range(T_NUM):
# シミュレート実行
list_active = simulate_population(NUM,
list_active,
percent_percolation,
percent_disapparence,
df_mem_links
)
list_timeSeries.append(list_active.copy())
print()
collect()
%%time
"""シミュレーションデータ"""
list_timeSeries_num = []
for i in range(len(list_timeSeries)):
list_timeSeries_num.append(sum(list_timeSeries[i]))
print()
collect()
%%time
"""実データ"""
T_NUM = len(df_mem_info.columns) - 1
list_timeSeries_num_real = []
for t in range(0, T_NUM):
list_timeSeries_num_real.append(len(df_mem_info[df_mem_info[str(t)] == 1].index))
print()
collect()
%%time
# 描画
plt.plot(list_timeSeries_num, label = 'simulated')
plt.plot(list_timeSeries_num_real, label = 'real')
plt.xlabel('month')
plt.ylabel('population')
plt.legend(loc = 'lower right')
# グラフを保存
plt.savefig('Knock79.png')
plt.show()
print()
collect()
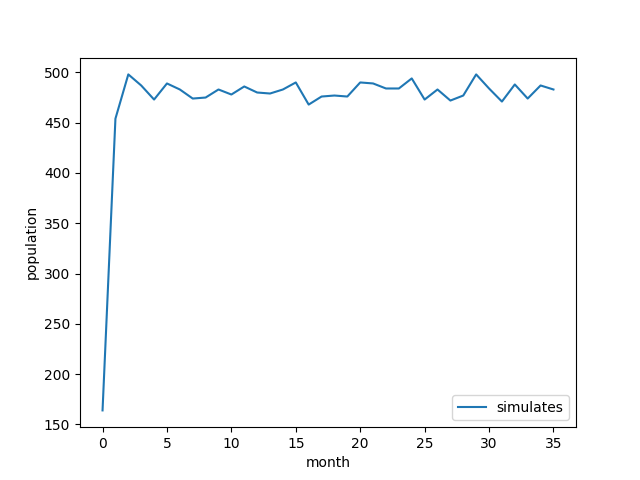
Knock80:シミュレーションによる将来予測を実施する
%%time
percent_percolation = 0.039006364196263604
percent_disapparence = 0.10147163541419416
T_NUM = 36
NUM = len(df_mem_links.index)
list_active = np.zeros(NUM)
list_active[0] = 1
list_timeSeries = []
for t in range(T_NUM):
list_active = simulate_population(NUM,
list_active,
percent_percolation,
percent_disapparence,
df_mem_links
)
list_timeSeries.append(list_active.copy())
print()
collect()
%%time
list_timeSeries_num = []
for i in range(len(list_timeSeries)):
list_timeSeries_num.append(sum(list_timeSeries[i]))
print()
collect()
%%time
# 描画
plt.plot(list_timeSeries_num, label = 'simulates')
plt.xlabel('month')
plt.ylabel('population')
plt.legend(loc = 'lower right')
# グラフを保存
plt.savefig('Knock80.png')
plt.show()
print()
collect()
ご協力のほどよろしくお願いします。
Discussion