Zenn
🧠

【Python】scikit-learnを用いたパーセプトロンモデルの訓練

2024/03/18に公開
scikit-learn
機械学習
Python 3
perceptron
パーセプトロン
tech

はじめに

この記事は株式会社インプレスの「Python機械学習プログラミング Pytorch&scilit-learn編」を読んで、私が学習したことをまとめています。
今回は3章2節の「scikit-learn活用へのファーストステップ：パーセプトロンの訓練」を読んで学んだことをまとめていきます。


【リンク紹介】
・【一覧】Python機械学習プログラミング Pytorch&scilit-learn編
・これまで書いたシリーズ記事一覧

第２章では分類のための学習アルゴリズムとしてパーセプトロンとADALINEを学びましたが、今回はscikit-learnライブラリ利活用の導入として、パーセプトロンの実装を行っていきます。用いるデータはIrisデータセットです。

インポート

# 場合によってインストール
pip install colorama > /dev/null

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.metrics import accuracy_score            # 正解率
from sklearn.linear_model import Perceptron           # パーセプトロンモデル
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split  # データセットの分割
from matplotlib.colors import ListedColormap

Irisデータセットの準備

# Irisデータセットをロード
iris = datasets.load_iris()

# データセットの確認
print(iris)

# 特徴量の取得
# 150個のデータの2, 3行目(花びらの長さと花びらの幅)を抽出
X = iris.data[:, [2, 3]]

# 目的変数の取得
y = iris.target
# 目的変数のunique値（以後正解ラベルという）を確認する
print('Class labels:', np.unique(y))

訓練データセットとテストデータセットに分割する

# データセットの分割
X_train, X_test, y_train, y_test = train_test_split(X, y,
                                                    test_size    = 0.3,    # 全体の30%をテストデータとする
                                                    random_state = 1,      # 乱数を固定
                                                    stratify     = y)      # 層化抽出を実行

上の分割作業の中で引数statify = yと指定しましたが、これは層化抽出を行う指示となります。これで正解ラベルのバランスを維持してデータセットを分割することができ、今回はIris-setosa(= 0)、Iris-versicolor(= 1)、 Iris-virginica(= 2)の比率は1:1:1であるので、以下の出力の通り分割されたどのデータも比率を保っていることが確認できます。

print('Labels counts in y:', np.bincount(y))
print('Labels counts in y_train:', np.bincount(y_train))
print('Labels counts in y_test:', np.bincount(y_test))
実行結果
Labels counts in y: [50 50 50]
Labels counts in y_train: [35 35 35]
Labels counts in y_test: [15 15 15]

訓練データを標準化する

前回と同様に、モデル学習の前に訓練データを標準化させていきますが、今回はscikit-learnのpreprocessingモジュールのStandardScalerクラスを使います。

# インスタンス化
sc = StandardScaler()

# 学習し、特徴量毎の平均値と標準偏差を推定する
sc.fit(X_train)

# 推定した平均値と標準偏差を用いて標準化を行う
X_train_std = sc.transform(X_train)
X_test_std  = sc.transform(X_test)

パーセプトロンモデルによる学習を行う

それでは早速パーセプトロンを用いて学習を行っていきます。

# 学習率0.1でパーセプトロンのインスタンスを生成
ppn = Perceptron(eta0 = 0.1, random_state = 1)

# 学習を実施
ppn.fit(X_train_std, y_train)

次にpredictメソッドを用いて予測を行います。

# テストデータで予測を実施
y_pred = ppn.predict(X_test_std)

# 誤分類したデータ点の個数を表示
print('Misclassified examples: %d' % (y_test != y_pred).sum())

予測値と正解値を用いて正解率を算出してみましょう。

# 分類の正解率を表示
print('Accuracy: %.3f' % accuracy_score(y_test, y_pred))
# パーセプトロンに定義されているscoreメソッドを用いて正解率を求めることも可能
# sklearn.linear_model.Perceptronライブラリ：https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.Perceptron.html
print('Accuracy: %.3f' % ppn.score(X_test_std, y_test))

実行結果
Accuracy: 0.978
Accuracy: 0.978

決定境界を可視化するための関数の実装

最後にplot_decision_regions関数を用いてパーセプトロンの決定領域を描画していきます。テストデータセットのデータ点を強調するために少し工夫を行います。

def plot_decision_regions(X, y, classifier, test_idx = None, resolution = 0.02):

    """マーカーとカラーマップの準備"""
    markers = ('o', 's', '^', 'v', '<')
    colors  = ('#3F9877',                  # ジェードグリーン
               '#003F8E',                  # インクブルー
               '#EA5506',                  # 赤橙
               'gray',
               'cyan'
              )
    cmap    = ListedColormap(colors[: len(np.unique(y))])

    """グリッドポイント（格子点）の生成"""    
    # x軸方向の最小値、最大値を定義
    x_min = X[:, 0].min() - 1
    x_max = X[:, 0].max() + 1
    # y軸方向の最小値、最大値を定義
    y_min = X[:, 1].min() - 1
    y_max = X[:, 1].max() + 1

    # 格子点の生成
    xx, yy = np.meshgrid(np.arange(x_min, x_max, resolution),
                         np.arange(y_min, y_max, resolution)
                        )
    # 確認用
    #print(xx1)
    #print(xx2)

    """各特徴量を1次元配列に変換(ravel())して予測を実行"""
    # つまり2つの特徴量から0と予測された格子点と1と予測された値が格子点ごとにlabに格納される
    lab = classifier.predict(np.array([xx.ravel(), yy.ravel()]).T)

    # 確認用
    #print(np.array([xx1.ravel(), xx2.ravel()]).T)
    #print(lab) # 格子点の並びで0,1が格納されているが、この時点では1次元配列なので変換が必要

    """予測結果の元のグリッドポイント(格子点)のデータサイズに変換"""
    lab = lab.reshape(xx.shape)

    """グリッドポイントの等高線のプロット"""
    plt.contourf(xx, yy, lab,
                 alpha = 0.3,                    # 透過度を指定
                 cmap  = cmap
                 )
    plt.xlim(xx.min(), xx.max())
    plt.ylim(yy.min(), yy.max())

    """決定領域のプロット"""
    # クラスごとに訓練データをセット
    for idx, cl in enumerate(np.unique(y)):
        plt.scatter(x         = X[y == cl, 0],
                    y         = X[y == cl, 1],
                    alpha     = 0.8,
                    c         = colors[idx],
                    marker    = markers[idx],
                    label     = f'Class {cl}',
                    edgecolor = 'black'
                    )
        
    """テストデータ点を目立たせる（点を〇で表示）"""
    if test_idx:    # ここはbool(test_idx)と同義。つまりTrueを返す
        # すべてのデータ点を描画
        X_test = X[test_idx, :]
        y_test = y[test_idx]

        plt.scatter(X_test[:, 0],
                    X_test[:, 1],
                    c         = 'none',
                    edgecolor = 'black',
                    alpha     = 1.0,
                    linewidth = 1,
                    marker    = 'o',
                    s         = 100,
                    label     = 'Test set'
                   )

if test_idx について

参考資料：bool関数の使い方(オブジェクトが真か偽か判定する)

決定境界を可視化

# 訓練データとテストデータの特徴量を行方向に結合
X_combined_std = np.vstack((X_train_std, X_test_std))
# 訓練データとテストデータのクラスラベルを結合
y_combined     = np.hstack((y_train, y_test))

# 決定領域をプロット
plot_decision_regions(X          = X_combined_std,
                      y          = y_combined,
                      classifier = ppn,
                      test_idx   = range(105, 150)
                     )

plt.xlabel('Petal length [standardized]')
plt.ylabel('Petal width [standardized]')
plt.legend(loc = 'upper left')
plt.tight_layout()

# グラフを保存
plt.savefig('fig3-1.png')

plt.show()

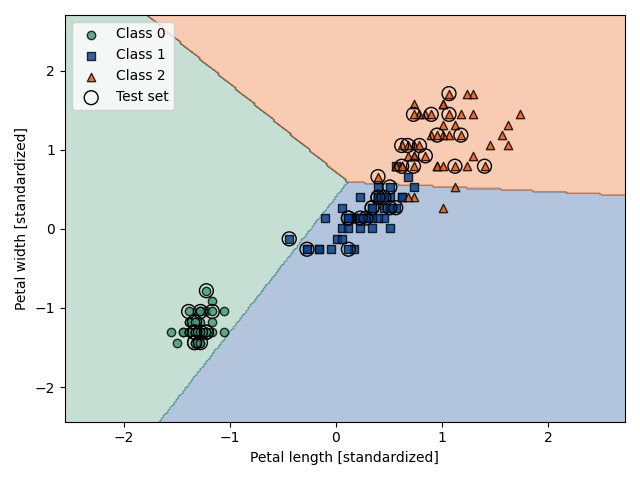
決定境界を可視化しましたが、やはり線形分離ができないデータセットにおいて、パーセプトロンアルゴリズムは収束できません。この問題点を改善する分類器として、ロジスティック回帰を考えていきいます。

参考文献

\bf{\textcolor{red}{記事が役に立った方は「いいね」を押していただけると、すごく喜びます \ 笑}}
ご協力のほどよろしくお願いします。

Discussion