🧩

【Java】バブルソート

2024/11/28に公開

この記事は、「新・明解Javaで学ぶアルゴリズムとデータ構造」を読んで学んだことを、個人的な備忘録目的でまとめています。
ただし、本を参考にして自分なりに構成やコードを変更しているためご注意ください。

アルゴリズムの詳細や解説は是非参考書をお手に取って読まれてください。
【リンク紹介】

・Javaで学ぶアルゴリズムとデータ構造

・これまで書いたシリーズ記事一覧

 基本用語確認
 アルゴリズム問題を解くためのものであって、明確に定義され、順序付けられた有限個の規則からなる集合。

（「JIS X0001」より。JISとは日本産業規格のこと。）

 バブルソート_基本形隣り合う2つの要素の大小関係を調べ、適宜交換を繰り返すアルゴリズム。

 基本形の実装//--- 配列の要素a[idx1]とa[idx2]の値を交換 ---//
static void swap(int[] a, int idx1, int idx2) {
  int   t = a[idx1];
  a[idx1] = a[idx2];
  a[idx2] = t;
}

//--- バブルソート ---//
static void bubbleSort(int[] a, int n) {
  
  // ソートのたびに操作する配列の幅を左から狭める
  for (int i = 0; i < n - 1; i++) {

    // 配列の右側から順番にソート
    for (int j = n - 1; j > i; j--) {
      
      if (a[j - 1] > a[j]) {
        // 配列の要素a[j - 1]とa[j]の値を交換
        swap(a, j - 1, j);
        
      }
    }
  }
}

 アルゴリズムのイメージ図

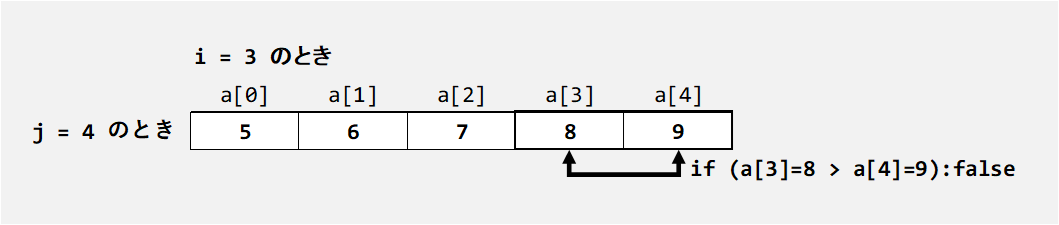
 基本形の利用例import java.util.Scanner;

//--- バブルソート（基本形） ---//
public class BubbleSort {

  //--- 配列の要素a[idx1]とa[idx2]の値を交換 ---//
  static void swap(int[] a, int idx1, int idx2) {
    int t = a[idx1];
    a[idx1] = a[idx2];
    a[idx2] = t;
  }

  //--- バブルソート ---//
  static void bubbleSort(int[] a, int n) {

    // ソートのたびに操作する配列の幅を左から狭める
    for (int i = 0; i < n - 1; i++) {

      // 配列の右側から順番にソート
      for (int j = n - 1; j > i; j--) {

        if (a[j - 1] > a[j]) {
          // 配列の要素a[j - 1]とa[j]の値を交換
          swap(a, j - 1, j);

        }
      }
    }
  }

  public static void main(String[] args) {
    Scanner stdIn = new Scanner(System.in);

    System.out.println("単純交換ソート（バブルソート）");
    System.out.print("要素数：");
    int nx = stdIn.nextInt();
    int[] x = new int[nx];

    for (int i = 0; i < nx; i++) {
      System.out.print("x[" + i + "]：");
      x[i] = stdIn.nextInt();
    }

    // バブルソートを実行
    bubbleSort(x, nx);

    System.out.println("昇順にソートしました。");

    for (int i = 0; i < nx; i++)
      System.out.println("x[" + i + "]=" + x[i]);
  }
}

 実行結果単純交換ソート（バブルソート）
要素数：5
x[0]：8
x[1]：7
x[2]：6
x[3]：5
x[4]：9
昇順にソートしました。
x[0]=5
x[1]=6
x[2]=7
x[3]=8
x[4]=9

 バブルソート_改良１ある配列の要素のソート時に、一度も交換されなかった場合、配列のソートを終了する。

 改良１の実装//--- バブルソート ---//
static void bubbleSort(int[] a, int n) {
  
  // ソートのたびに操作する配列の幅を左から狭める
  for (int i = 0; i < n - 1; i++) {

    // 交換回数
    int exchg = 0;

    // 配列の右側から順番にソート
    for (int j = n - 1; j > i; j--) {
      
      if (a[j - 1] > a[j]) {
        
        // 配列の要素a[j - 1]とa[j]の値を交換
        swap(a, j - 1, j);
        exchg++;
      }
    }
    
    // 交換が行われなかったら終了
    if (exchg == 0) break;
  }
}


 アルゴリズムのイメージ図

 改良１の利用例基本形の利用例のbubbleSortメソッドの記述を、改良１の実装におきかえればよい。

 実行結果単純交換ソート_改良１（バブルソート）
要素数：5
x[0]：6
x[1]：5
x[2]：7
x[3]：8
x[4]：9
昇順にソートしました。
x[0]=5
x[1]=6
x[2]=7
x[3]=8
x[4]=9

 バブルソート_改良２配列の要素の交換が行われた際、ソート後の一番最後の要素の位置を記録することで、以降の配列の要素のソート時に既にソート完了した配列を無視する。

 改良２の実装//--- バブルソート ---//
static void bubbleSort(int[] a, int n) {

  // a[k]より前はソート済み
  int k = 0;

  while (k < n - 1) {

    // ソート後の一番最後の要素の位置
    int last = n - 1;

    // 配列の右側から順番にソート
    for (int j = n - 1; j > k; j--) {

      if (a[j - 1] > a[j]) {
        // 配列の要素a[j - 1]とa[j]の値を交換
        swap(a, j - 1, j);
        last = j;
      }
    }

    // lastをkに格納
    k = last;
  }
}

 アルゴリズムのイメージ図

 改良２の利用例基本形の利用例のbubbleSortメソッドの記述を、改良２の実装におきかえればよい。

 実行結果単純交換ソート_改良2（バブルソート）
要素数：5
x[0]：5
x[1]：6
x[2]：9
x[3]：7
x[4]：8
昇順にソートしました。
x[0]=5
x[1]=6
x[2]=7
x[3]=8
x[4]=9
\bf{\textcolor{red}{記事が役に立った方は「いいね」を押していただけると、すごく喜びます \ 笑}}

ご協力のほどよろしくお願いします。