[Python] ReLU活性化関数の理解を深めよう
はじめに
Deep learningに非線形性を導入する活性化関数として人気の関数であるReLUの性質とそれを使う利点と欠点をまとめました。理解を深める助けになれば幸いです。
参考資料
ReLU活性化関数の性質
ReLU(Rectified linear unit)は日本語では整流化線形ユニットと呼ばれ、下記の3つの問題を解消する活性化関数としてDeep learningにおいて最も人気のある活性化関数の1つ。
- モデルに非線形の特性を導入
- 勾配消失問題を解決
- 飽和問題の解決
Sigmoid関数やtanh関数も微分可能で人気のある活性化関数だったけど勾配消失問題や飽和問題を抱えている。これらの関数でなぜこの2つの問題が起きるかはこの記事の最後のSigmoidとtanhの問題点で説明する。これらの問題を解決する活性化関数としてReLU関数がよく使われるようになった。
ReLU関数は次の式で表すことができる。
ReLU(x) = max(0,x)
下のReLUとReLUの導関数のグラフを見てわかるように、ReLUは入力が0以下であれば0を返し0より大きければその値をそのまま返す。またx=0では微分できない性質を持つので誤差逆伝播法で学習させる場合はx=0の勾配は0にして導入される。
Graph描画のソースコード
import numpy as np
import matplotlib.pyplot as plt
def relu_function(x):
return np.maximum(0,x)
def differentiate(f, x):
h = 1e-4
return (f(x+h) - f(x-h))/2*h
x = np.linspace(-5,5,100)
relu = relu_function(x)
derivative_relu = differentiate(relu_function, x)
fig = plt.figure()
ax = fig.add_subplot(211)
ax.plot(x,relu)
plt.title('ReLU')
ax = fig.add_subplot(212)
ax.plot(x,derivative_relu)
plt.title('Derivative of ReLU')
plt.tight_layout()
plt.savefig("relu.png")
plt.show()

ReLUがなぜ良い活性化関数なのか?
計算が単純である
Sigmoidやtanhなどの関数にはexpの計算が含まれているが、ReLUはmax関数の演算だけなので計算コストが軽く学習速度が早い。
表現スパース性がある
スパースは、データや特徴表現が少数の要素(非ゼロまたは有意な要素)で構成される性質のこと。これはSigmoidやtanhなどの関数とは違い、ReLUを活性化関数として用いると不必要な情報に対しては真の0を出力できることで実現される。この性質は不必要な項目は取り除いてモデルを単純にでき、また、学習速度を上げることにもつながるので機械学習において望ましい性質。
線形的な振る舞い
ReLUは非線形関数でありながらも、あくまで2つの線形な関数を結合した形なので線形モデルの利点も活かされる。それは上で見たような計算速度の速さや学習後の重みからどの情報が重要なのかが把握しやすくなるなどの利点がある。一方発展的な課題でも見るがReLUにも問題点はあるので学習後のモデルの評価に気をつける必要はある。
幅広いモデルに適用可能
以下のようにメジャーなモデルに対してはよく使われているようだ
- Convolutional Neural Networks (CNNs)
- AlexNe
- VGGNe
- ResNet
- MobileNet
- Recurrent Neural Networks (RNNs)
- LSTM
- GRU
- Feedforward Neural Networks
- MLP
- Generative Adversarial Networks (GANs)
発展的な話題
ReLUの負の領域での値と勾配が0である性質は利点でもあり欠点でもあり、それによって下記の問題が発生するので注意が必要。
Dead ReLU
ReLUを浅いレイヤーで使用する際に、負の入力に対して出力がゼロになる性質から情報の損失が発生する可能性がある。これと関係して、一部のニューロンが学習中に非活性になり、そのニューロンは以後どのような入力が与えられてもゼロを出力するようになり、これをニューロンの非活性化と呼ぶ。この問題を解決するために、ReLUを変形させたLeaky ReLU、Parametric ReLU (PReLU)、Exponential Linear Unit (ELU)などを用いる方法もあるが、前節で見た利点である表現スパース性が弱くなる。
ネットワークの深層化による勾配消失問題再発
層が深くなるほど有益な情報の信号が0になってしまうリスクは高まるのであろう。
締め
ReLUの性質と利点と欠点についてみてきた。Sigmoid関数やtanh関数の問題点を解決しつつ他にもモデルの単純化や計算速度などに貢献してくれる活性化関数であることが分かった。ただし、欠点もあるので歴史的にSigmoid関数 -> tanh関数 -> ReLU関数と世代交代してきたようにReLU関数 -> ?となることもあると思うのでその辺りは注視していきたい。
Sigmoidとtanhの問題点
これらの関数を活性化関数として用いる際の問題点は次の2つ
- 勾配消失問題
- 飽和問題
勾配消失問題は、誤差逆伝播法でのモデルの学習の際に途中のレイヤーで誤差が0に近い値を持つレイヤーがあるとパラメータへの補正値がほぼ0になってしまい学習が進まなくなる問題のこと。飽和問題は、モデルの推論時に優位な情報を含む大きな入力値が、活性化関数で処理されることによって活性化関数の上限値と下限値である値(例えば1や-1や0)にまで抑えられてしまい優位な情報を伝達できなくなってしまう問題のこと。実はSigmoid関数とtanhの関数形(下のグラフ)を見ると分かるが、この2つの問題は関係し合っていて、関数の値がある値に漸近して飽和してしまうことで勾配が小さくなる関係があることがわかる。それも有ってか問題点として挙げられるのは勾配消失問題が多いようだ。
この節ではSigmoid関数とtanh関数でこの問題が発生しうることを見る。
Sigmoid関数の場合
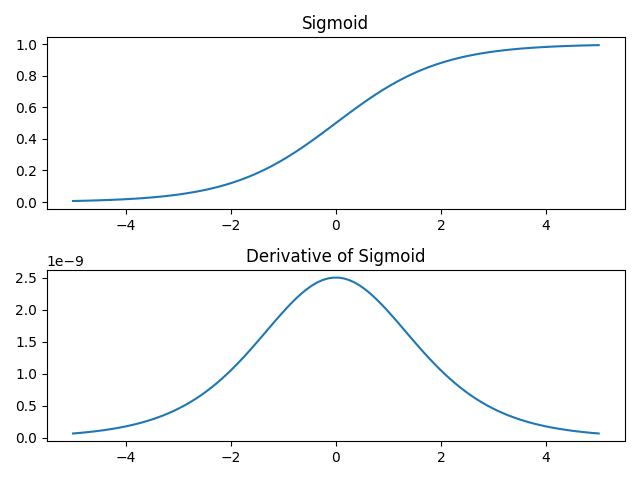
Sigmoid関数の関数形は下の式で表される非線形な関数であるが、勾配消失問題の原因は、入力値xの絶対値が大きくなると導関数の値が0に漸近する(元の関数が飽和して勾配が小さい)ことである。
Sigmoid(x) = 1 / (1 + exp(-x))
Graph描画のソースコード
import numpy as np
import matplotlib.pyplot as plt
def sigmoid_function(x):
return 1 / (1 + np.exp(-x))
def differentiate(f, x):
h = 1e-4
return (f(x+h) - f(x-h))/2*h
x = np.linspace(-5,5,100)
sigmoid = sigmoid_function(x)
derivative_sigmoid = differentiate(sigmoid_function, x)
fig = plt.figure()
ax = fig.add_subplot(211)
ax.plot(x,sigmoid)
plt.title('Sigmoid')
ax = fig.add_subplot(212)
ax.plot(x,derivative_sigmoid)
plt.title('Derivative of Sigmoid')
plt.tight_layout()
plt.savefig("sigmoid.png")
plt.show()
tanh関数の場合
tanh関数はSigmoid関数に線形変換を行なって次のように書ける。下のグラフでは完全に重なってしまっているのでソースコード内のコメント"# 0.05"をコメントインすると少しずらしてプロットできて関数形が重なっていたことを確認できる。
tanh(x) = 2 * Sigmoid(2x) - 1
つまり、tanh関数とSigmoid関数は同じ性質を持つので先ほど見たSigmoid関数と同じ問題点を抱えていることがわかる。
Graph描画のソースコード
import numpy as np
import matplotlib.pyplot as plt
def sigmoid_function(x):
return 1 / (1 + np.exp(-x))
x = np.linspace(-5,5,100)
tanh = np.tanh(x)
converted_sigmoid = 2 * sigmoid_function(2*x) - 1 # + 0.05
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(x,tanh)
ax.plot(x,converted_sigmoid)
plt.title('tanh & converted Sigmoid')
plt.savefig("tanh_and_converted_sigmoid.png")
plt.show()

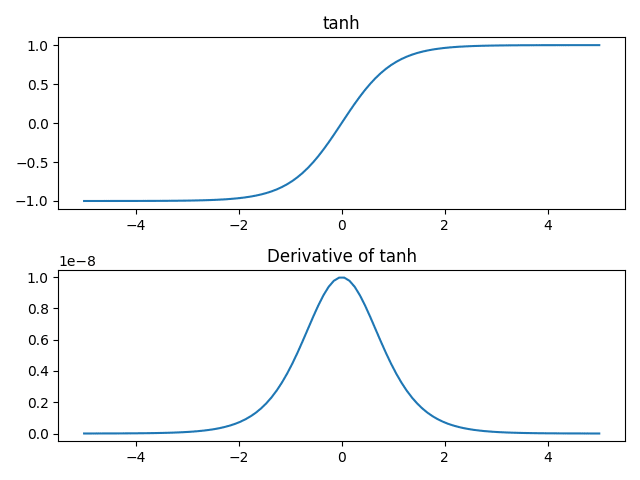
一応参考のためにtanh関数とその導関数のグラフも書いておく。
Graph描画のソースコード
import numpy as np
import matplotlib.pyplot as plt
def differentiate(f, x):
h = 1e-4
return (f(x+h) - f(x-h))/2*h
x = np.linspace(-5,5,100)
tanh = np.tanh(x)
derivative_tanh = differentiate(np.tanh, x)
fig = plt.figure()
ax = fig.add_subplot(211)
ax.plot(x,tanh)
plt.title('tanh')
ax = fig.add_subplot(212)
ax.plot(x,derivative_tanh)
plt.title('Derivative of tanh')
plt.tight_layout()
plt.savefig("tanh.png")
plt.show()
Discussion