Zenn
🐒

Stanford NLP with Deep Learning Lecture6のまとめ(後編)

2023/05/30に公開
ディープラーニング
機械学習
初心者
#
NLP
#
nn
tech

1.はじめに

本稿は前稿に引き続きLecture6の後半部分についてまとめていきたいと思います。
そのため、前半部分で述べた内容を知っている前提で述べていくので、よければ前編を見てから本記事を読んでいただけると幸いです。

2.RNNと勾配消失問題

前編では勾配消失問題を最後に取り扱いました
勾配消失問題はRNNに限らず、他のNNモデルにおいても同様に気をつけるべき課題の一つです。
そのため各NNモデルでは勾配消失を防ぐための工夫がモデル内に組み込まれています。
<代表例>

  1. Residual connections(ResNet)
    :残差ブロックと呼ばれる入力情報を出力情報に直接渡すというブロックを繰り返し行う手法(図3参照)
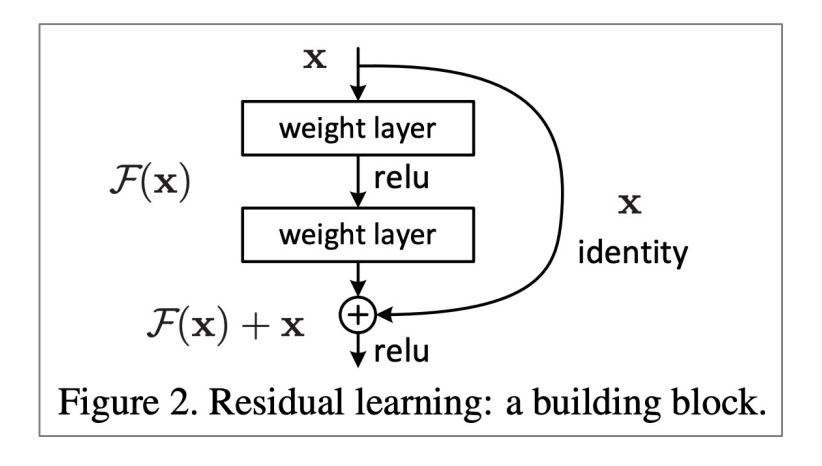    図1)ResNetにおける残差接続([3]より引用)

  2. Dense connections(DenseNet)
    :残差接続がブロック内で入力を出力に渡すのと違い、dense connectionsは各レイヤーをそれ以降のレイヤーの出力に加えるという手法(図4参照)
    図2)DenseNetにおけるdense connetions([4]より引用)

  3. Highway connections(Highway Net)
    :この後述べるLSTMにインスパイアを受けて提案された手法で入力を複数のゲートを通して活性化関数に入れるという手法
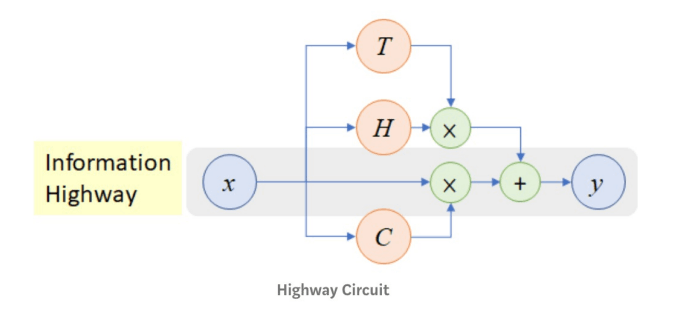    図3)HighwayNetにおけるHighway connections([5]より引用)

これらと比較してRNNは隱れ層間で以下式で分かる通り、等しい重みW_hと前の隠れ層の出力を使ってそれ以前の入力を記憶しているため、系列長の長さが長くなると勾配消失問題の影響を受けやすいです。

3.LSTM(Long Short-Time Memory)

3で述べたRNNにおける勾配消失問題への対策として「過去の情報を記憶した情報と隠れ層の出力をわけてみては?」という発想のもと生まれたモデルがLSTM(Long Short-Time Memory)です。
　このモデルは隠れ層の出力ベクトルであるhの他に、過去の情報を保有するcell stateベクトルcの二つを保有するという特徴を持っています。
　加えてこれらのベクトルをただ入力情報のもと二つに分けたのではなく、3つのゲートを用いて管理することで入力をもとに情報を更新するか否かの判断を行っています。(言い換えれば動的である)

3-1:LSTMの理解

<LSTMで用いられている各ゲートについて>

  1. forget gate
    :過去の情報を保つか否かを判断するゲート(2000年のLSTMに関する論文で追加されたゲート)
f^{(t)} = \sigma(\mathbf{W}_f \mathbf{h}^{(t-1)} + \ \mathbf{U}_f \mathbf{x}^{(t)} + \mathbf{b}_f) \tag{1}
  1. Input gate
    :cell state ベクトルを更新するか否かを判断するゲート
i^{(t)} = \sigma(\mathbf{W}_i \mathbf{h}^{(t-1)} + \ \mathbf{U}_i \mathbf{x}^{(t)} + \mathbf{b}_i) \tag{2}
  1. Output gate
    :cを出力hに対してどのくらい影響させるかを判断するゲート
o^{(t)} = \sigma(\mathbf{W}_o \mathbf{h}^{(t-1)} + \ \mathbf{U}_o \mathbf{x}^{(t)} + \mathbf{b}_o) \tag{3}

これら3つのゲートを用いることで過去の情報を保持したまま文章を理解することを可能にしました。
またRNNと異なり、ゲートごとで重みである\mathbf{W},\mathbf{U}やバイアスを表す\mathbf{b}は異なっています。

<LSTMにおけるアーキテクチャの数式>

  • cell　state の更新
\tilde{c}^{(t)} = \ tanh(\mathbf{W}_c\mathbf{h}^{(t-1)}+\mathbf{U}_c\mathbf{x}^{(t)}+\mathbf{b}_c) \tag{4}
  • 新しいcell stateの書き込み
\begin{align} & c^{(t)} = f^{(t)}\otimes c^{(t-1)}+i^{t}\otimes \tilde{c}^{(t)} \tag{5} \\ &[f^{(t)}\otimes c^{(t-1)}:過去の情報, i^{t}\otimes \tilde{c}^{(t)}:更新情報] \end{align}
  • 隠れ層の出力の算出
\begin{align} h^{(t)} = o^{(t)}\otimes tanh(c^{(t)}) \tag{6} \end{align}

<LSTMのアーキテクチャ図>
式(4), (5), (6)を図に表したものが以下の図4です。
これを入力のすべてのステップで行なっていきます。
図4)LSTMにおけるt地点の隠れ層の様子([6]より引用)

3-2:勾配消失問題とLSTM

先述した通り、RNNは過去の情報を各層で共通した値を持つ重みと前の層の情報を用いて過去の情報を記憶していました。これは系列長の長さが大きくなるにつれて勾配消失問題の影響を受けて、初めの方の情報を保持するのが困難でした。
　それに対してLSTMはモデルの出力そのものに過去の情報を記憶しているcell stateベクトルであるcを用いて保持することができるためRNNと比較して容易であることは自明です。また過去の情報を保存する度合いを決めるのに確率を用いているため、保存度合いも変動させることができます。
　ここまでいうと勾配問題が全く起こらないふうに聞こえますが、一概にそうとは言えず保証はされていないことは留意する必要があります。

4.Bidirectional Model

これまで述べてきたRNNやLSTMは順方向に与えられた文章を入力としていました。
　しかし、このままだと複数意味を持つ単語において後ろの単語から意味がわかる状況に対応することができません。そのため逆方向から文章を理解したい!というのがこのBidirectional Modelのモチベーションとなっています。
今回は講義に則り、"Bidirectional RNNs"に焦点を合わせていきます。

4-1:Bidirectional RNNs

Bidirectional RNNsとはその名前の通り、双方向に解析を進めていくRNNsモデルとなっています。
このモデルの特徴としては、あるt地点の隠れ層において双方向から得たベクトルを結合することでt地点の隠れ層の出力として用いて、次の隠れ層に渡す際は繋げる前の順方向、逆方向それぞれの出力を用いています。(図5参照)

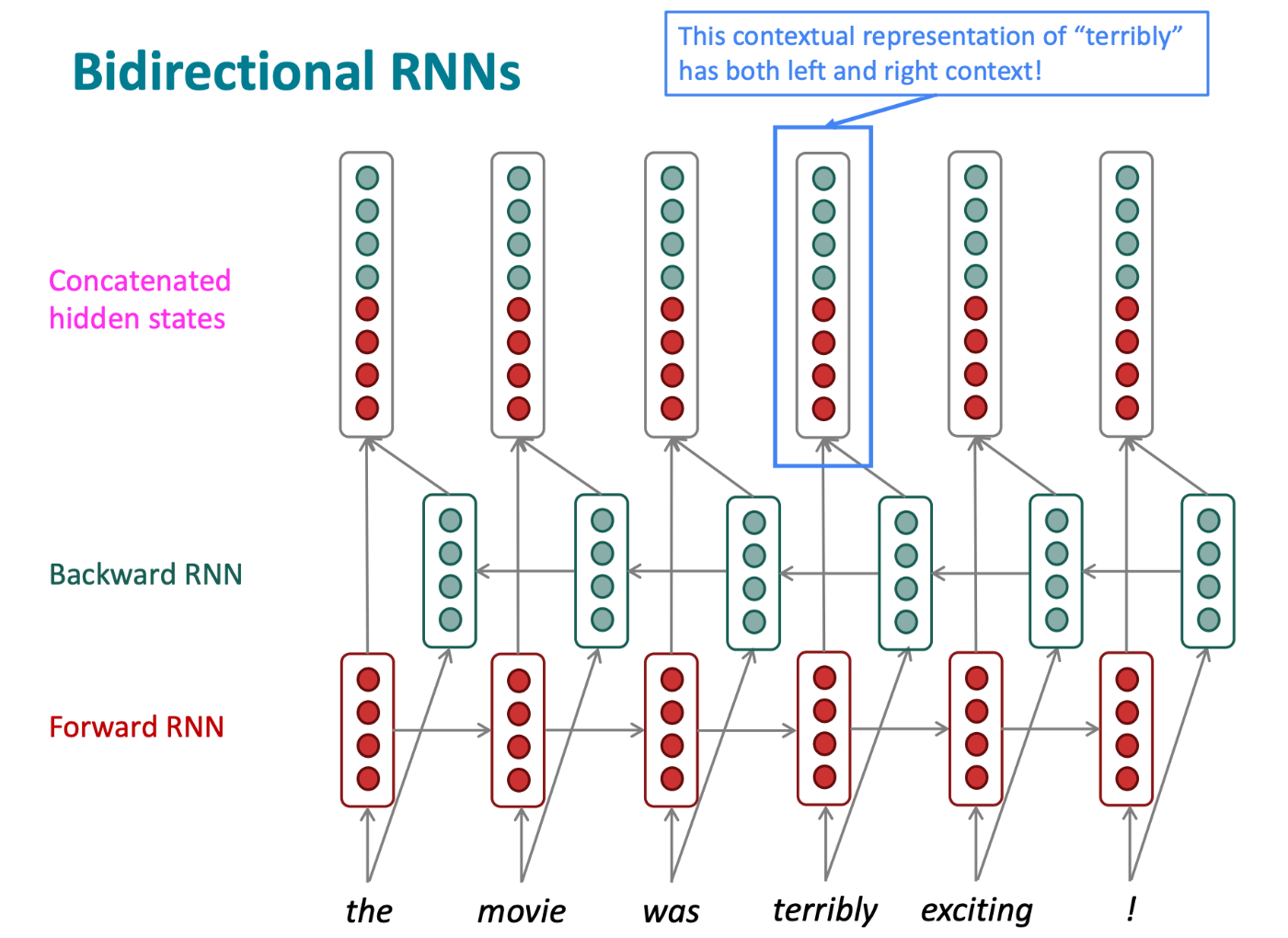図5)双方向RNNsのアーキテクチャ図

<数式>

\begin{align} &RNN(\mathbf{h}, \mathbf{x})=\sigma (\mathbf{W}_h \mathbf{h}^{(t-1)}+\mathbf{W}_x \mathbf{x}^{(t)} + \mathbf{b}_1)とする \\ &ForwardRNN \space\overrightarrow{\mathbf{h}}^{(t)} = RNN_{FW}(\overrightarrow{\mathbf{h}}^{(t-1)}, \mathbf{x}^{(t)}) \\ &BackwardRNN \space\overleftarrow{\mathbf{h}}^{(t)} = RNN_{BW}(\overleftarrow{\mathbf{h}}^{(t-1)}, \mathbf{x}^{(t)}) \\ &(2), (3)式を用いて \\ &結合部分 \space h^{(t)} = [\overrightarrow{\mathbf{h}}^{(t)};\overleftarrow{\mathbf{h}}^{(t)}] \end{align}

Bidirection　RNNsはRNNと異なっておりモデル全体で重みを共有しておらず各方向ごとに重みを持っています。
　また、双方向に解析を進めていくという性質上次の単語を予測することを目的としている言語モデルに用いることはできません。その代わりに感情分析やQAといった入力に完全な文章を用いるタスクにいついては有用です。
　なにより、この後でてくるTransformerベースモデルであるBERTにこの考え方が用いられてるため重要です。

5.まとめ

今回のLecture6は二部に分けて投稿しました。
LSTMはTransformerモデルまでが登場するまでかなりの精度を誇るモデルですが、その裏では勾配と戦っていた研究者の方々がいると思うと感謝しかないですね。
次はMulti layerとSeq2SeqのあとTransformerの講義に入っていくので引き続き努力していきたいと思います。

6.参考文献

[1]:Stanford CS224N NLP with Deep Learning | Winter 2021 | Lecture 6 - Simple and LSTM RNNs
[2]"Activation Functions in Deep Learning: A Comprehensive Survey and Benchmark",
Shiv Ram Dubey, Satish Kumar Singh, Bidyut Baran Chaudhuri 2021
[3]"Deep Residual Learning for Image Recognition", He et al, 2015.
[4]”Densely Connected Convolutional Networks", Huang et al, 2017
[5]”Highway Networks", Srivastava et al, 2015.
[6]CVMLエキスパートガイド

Discussion