Stanford NLP with Deep Learning Lecture6のまとめ(前編)

1.はじめに

今回もYoutubeに公開されているStanford大学のNLPの講義で自分が見返した時に必要だと思った点などを中心にまとめていきたいと思います。
Lecture6から本格的にDeep Learningの世界に入っており、今回はRNNとLSTMに焦点を合わせた内容となっていました。これまで学習していきたことの再確認とともに曖昧な部分の知識の補完ができたので体系的に学習するのはやはり大事だと思いました。
記事にする以上誤った情報は載せないよう精査しているつもりではありますが、今まで同様間違った点や理解しにくい言い回し等あればご指摘していただけると幸いです。

2.RNNを用いた言語モデル

2-1:RNNについて

深層学習モデルとしてまずはシンプルなRNNについて述べていきます。
そもそもRNN(Recurrent Neural Network), 日本語では回帰型ニューラルネットワークとはシーケンスデータに対して特化したニューラルモデルのことを指します。
　特徴としてはあるt地点の隠れ層における入力にt-1地点の出力を入力として用いるという点が挙げられます。これによって過去の情報をメモリとして保存できます。(図1参照)

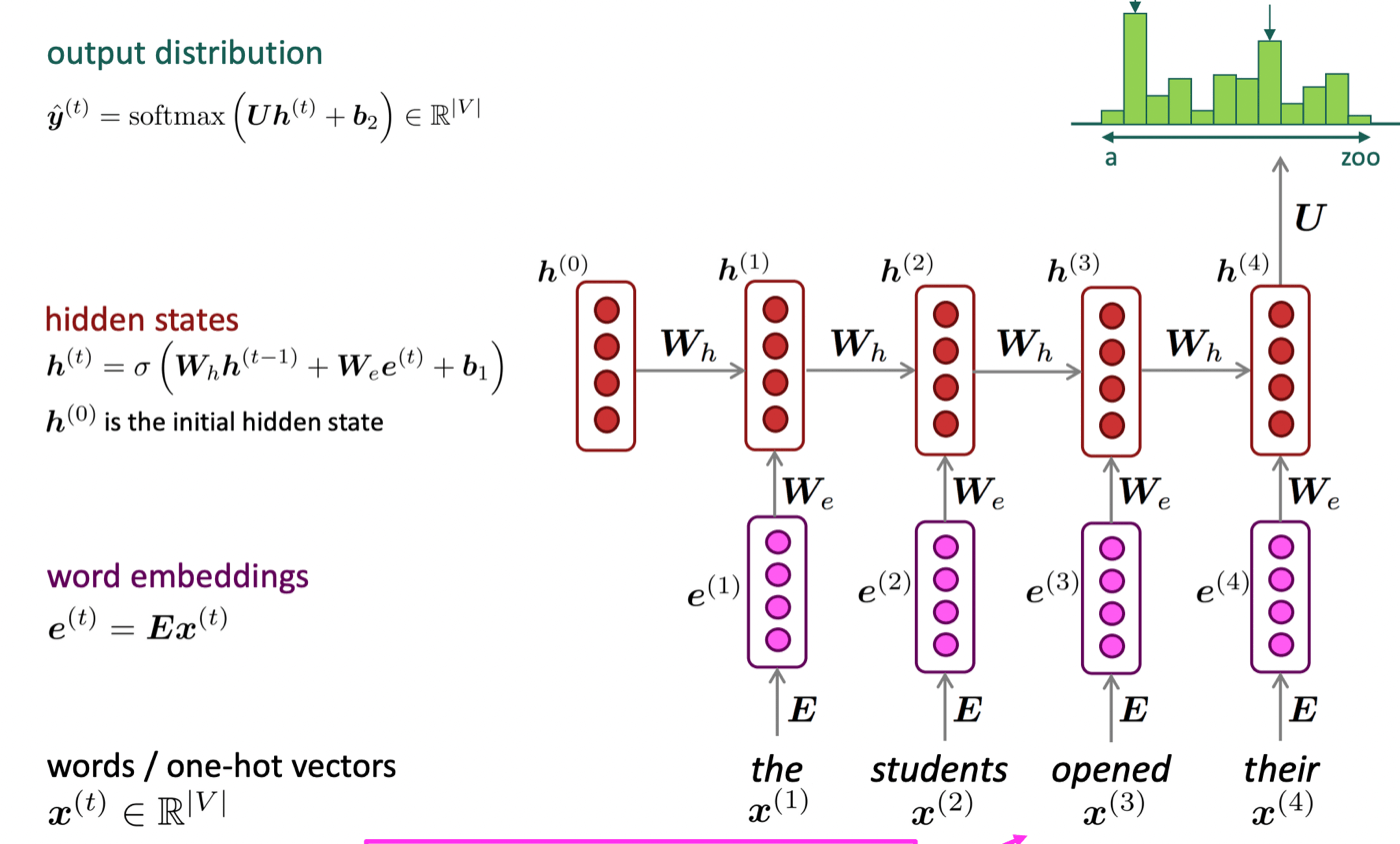図1) RNNのアーキテクチャ図([1]より引用)

RNNの流れとしては以下のようになっています。

1. 入力としてテキストデータをEmbeddingして得られたベクトルを隠れ層へ入力
2. 前のステップの隠れ層の出力と入力それぞれに重み付けを行い、活性化関数に代入しその層における出力となる(多くの場合tanhが用いられます。)
3. これを文末に到達するまで繰り返し行っていく
4. 最終層の出力をSoftmax関数で確率へと変換し、尤もらしい単語を選択する

2でtanh関数を用いる理由としてはNNにおいて、注視すべき要素の一つである勾配が消失するのを防ぐために用いられています。

2-2:RNN-LMの訓練

RNNを用いた言語モデルを学習させる際には他のモデル同様損失を用いてパラメータの更新を行っていきます。損失としては交差エントロピーがよく用いられます。

$$\begin{align} L^{(t)}(\theta) = -\displaystyle\sum_{w \in V}\mathbf{y}_w^{(t)}\log\hat{\mathbf{y}}_w^{(t)} = -\log\hat{\mathbf{y}}_{x_{t+1}}^{(t)} \tag{1} \\ [L:損失, \mathbf{y}:予測確率(ベクトル), V:\mathbf{y}の次元数] \end{align}$$

この式はあるt地点における損失を表しています。モデル全体の損失を考えるときは各ステップの損失の平均を取ります。

$$\begin{align} L(\theta) = \ \frac{1}{T}\sum_{t=1}^T L^{(t)}(\theta) = \ \frac{1}{T}\sum_{t=1}^T -\log\hat{\mathbf{y}}_{x_{t+1}}^{(t)} \tag{2} \\ [T:系列長] \end{align}$$

(1),(2)式の最終項に含まれる$\hat{\mathbf{y}}_{x_{t+1}}^{(t)}$はt地点における予測確率のうちt+1地点の単語に該当する次元に属する値を示しています。
よって、交差エントロピーはt地点の出力が実際のt+1番目の単語と近しい結果を得られたかを見ているということがわかります。
　このことからRNNは"Teacher forcing"であると言われます。
この損失の式$L(\theta)$を見て分かる通り、系列長が短い文章ならまだしも長い文章となると全ステップで損失を算出し、パラメータの更新を行うことは計算コストが高いため、確率的勾配降下法(SGD)を用いて計算量を削減します。
またあるt地点における隠れ層の重みである$W_h$の更新は以下式で行われます。

$$\frac{\partial L^{(t)}}{\partial{W_h}} = \sum_{i=1}^t \frac{\partial L^{(t)}}{\partial{W_h}}\bigg|_{(i)} \tag{3}$$

このようにあるt地点以前の勾配情報を合計したものをその地点のパラメータの更新に用いる逆伝播の手法をBack Propagation through timeと呼びます。
ただ、実際は1からtまで計算するのではなく、t-10からtまでの勾配情報を用いることが多いです。
また、これは重みが各層で共通しているという特徴に由来して成り立っています。(式(4)参照)

$$\begin{align} \frac{\partial L^{(t)}}{\partial{W_h}} &= \sum_{i=1}^t \frac{\partial L^{(t)}}{\partial{W_h}}\bigg|_{(i)} \frac{\partial{W_h}|_{(i)}}{\partial{W_h}} \\ &重みW_hは全ての層で等しいため\frac{\partial{W_h}|_{(i)}}{\partial{W_h}} = 1 \\ &ゆえに \\ & = \sum_{i=1}^t \frac{\partial L^{(t)}}{\partial{W_h}}\bigg|_{(i)} \tag{4} \end{align}$$

2-3:各層の情報利用

図1では出力に用いるのは最終層のベクトルのみとしましたが、一部の自然言語のタスクにおいては最終層のみならず中間層のベクトルを用いた方が精度がいい場合もあります。
これはNNが捉えている言語情報に由来しています。初めの方の隠れ層では言語の表層的な部分を理解し、最終層に近づくにつれて言語の深層的な部分を理解していくという特徴を持つためです。
代表例としては、

• Mean-Pooling
• Max-Pooling

の二つが挙げられます。

3.勾配消失・爆発問題

NNにおいて切っても切り離せない問題として、勾配消失問題と勾配爆発問題が挙げられます。
RNNも活性化関数にシグモイド関数ではなくtanh関数を用いているとは言え、系列長の長さが長くなるにつれて影響を受けます。
勾配消失問題:逆伝播の勾配計算の際に徐々に勾配が小さくなっていき、初めの情報を保てず学習がうまくいかない問題
勾配爆発問題:パラメータ更新の際に勾配が大きすぎると最適なパラメータの値を通り越して更新を行ってしまう問題

3-1:勾配爆発問題(exploding gradient a problem)

先述した通り、勾配爆発問題とはパラメータ更新の際に勾配が大きくなりすぎて最適解を見つけられず発散してしまうことでした。
これは、パラメータ以下式のように勾配と学習率の積を前の勾配から引いて次の勾配を求めることが原因となります。

$$\theta^{new} = \theta^{old}\nabla_{\theta}L(\theta)$$

勾配が大きすぎるのが問題なら小さくすれば良いと思うかもしれませんが、それだともう一つの問題である勾配消失問題につながってしまいます。
そこで、勾配爆発問題の対処法として採用されたのがGradient Clippingという勾配に対して閾値を設定してそれを超えると重みを課すという手法を取り入れました(図2参照)。

図2) Gradient Clippingのアルゴリズム([1]より引用)

勾配爆発問題は消失問題と比較すると対処は容易らしいです、、、まぁたしかにって感じですが。

3-2:勾配消失問題(vanishing gradient a problem)

次は勾配消失問題について述べていきます。
講義では例として活性化関数をただの恒等関数としたときで例を書かれてたので、私も同様にしていきます。(決して他の活性化関数の微分をmarkdownで書くのがめんどくさかったとかではありません決して、、、)

RNNにおけるあるt地点における隠れ層$h^{(t)}$は以下のように表されます。

$$h^{(t)} = \sigma(\mathbf{W}_h h^{t-1}+\mathbf{W}_x x^{(t)}+b_1)$$

今回は先ほども述べた通りσを恒等関数$\sigma(x) = x$として考えていきます。
まずこの後連鎖率の計算で用いる隱れ層間の偏微分を考えていきます。

$$\begin{align} \frac{\partial h^{(t)}}{\partial h^{(t-1)}} &= \ diag(\sigma(\mathbf{W}_h h^{t-1}+\mathbf{W}_x x^{(t)}+b_1))\mathbf{W}_h \\ &= \mathbf{I}\mathbf{W}_h \\ &= \mathbf{W}_h \\ \tag{5} &[I:単位行列] \end{align}$$

次に損失$L(\theta)$の勾配を考えていきます。
i地点における損失の勾配をj地点に対して考えていきます(j < i)

$$\begin{align} \frac{\partial L^{(i)}(\theta)}{\partial \mathbf{h}^{(j)}(\theta)} \ &= \frac{\partial L^{(i)}(\theta)}{\partial \mathbf{h}^{(i)}(\theta)} \ \prod_{j \leq t \leqq i} \frac{\partial h^{(t)}}{\partial h^{(t-1)}} \\ &(5)式より \\ &= \frac{\partial L^{(i)}(\theta)}{\partial \mathbf{h}^{(i)}(\theta)} \ \prod_{j \leq t \leqq i}\mathbf{W}_h \\ &= \frac{\partial L^{(i)}(\theta)}{\partial \mathbf{h}^{(i)}(\theta)}\mathbf{W}_h^l \\ &[l:i-j] \tag{6} \end{align}$$(6)

これを防ぐために(5)式の値が小さくなることを防ぎながら勾配爆発問題が起こらないようにtanh関数やReLU関数といったさまざまな活性化関数が利用されています。
　活性化関数については2の論文で詳しく書かれているので一読の価値はあると思うのでおじかなる時にぜひ！
　簡単にいうと勾配の最大値を以下に1に保つか、そして1にならないときをどう表現するかの工夫がそれぞれの活性化関数で行われています。

4.まとめ

Lecture6はNLPにおけるDeep Learningのはじめということでかなり密度の高い内容となっていました。
そのため一稿で書くには長い記事になって、個人的に長い記事は情報量のわりに身につかないと思うので二稿に分けたいと思います。
次はLSTMと現在の文章の特徴量かにおいてデファクトスタンダードであるBERTにもつながるBidirectionRNNについて述べていきたいと思います。気になった方は後編も見ていただければ幸いです。

5.参考文献

[1]:Stanford CS224N NLP with Deep Learning | Winter 2021 | Lecture 6 - Simple and LSTM RNNs
[2]"Activation Functions in Deep Learning: A Comprehensive Survey and Benchmark",
Shiv Ram Dubey, Satish Kumar Singh, Bidyut Baran Chaudhuri 2021