📍
S2 Geometry Libraryを利用し、ある地点の緯度経度よりその地点を含むS2セルを求める方法
S2 Geometry Libraryとは
- 地球を球面と見たときにS2セルと呼ばれる領域に分割していき、各セルにcell IDと呼ばれる値を割り当てるGoogleが2017年に出したジオメトリ系のライブラリです。参照
S2セルとは
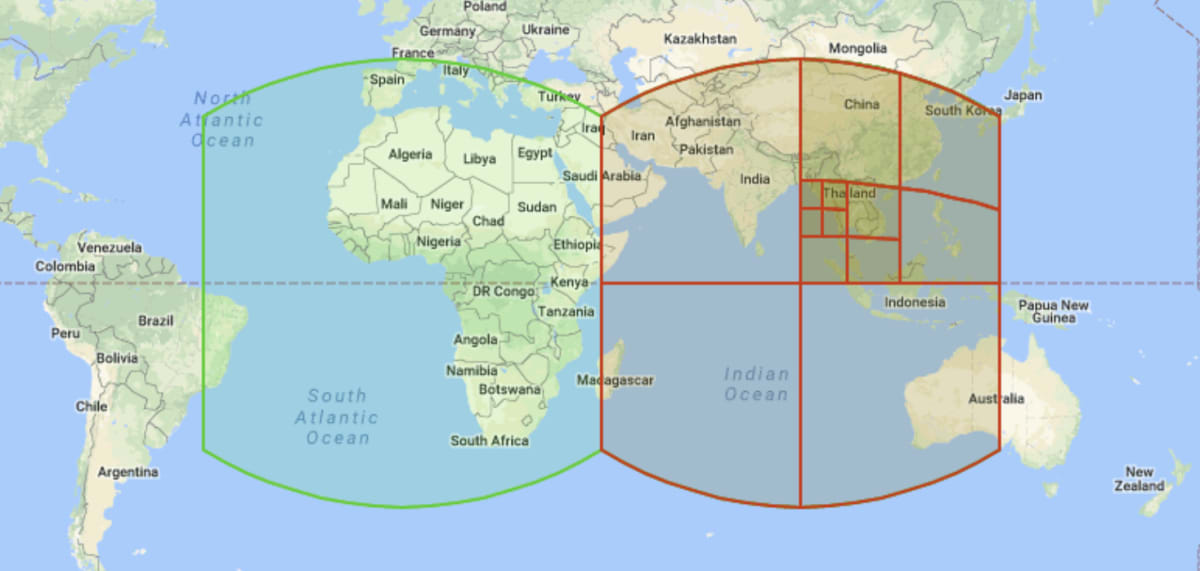
- S2セルとは、地球の表面を特定の大きさで均等に分けたものです。
- 緯度経度のような点ではなく、面で位置を表します。
S2セルのレベル
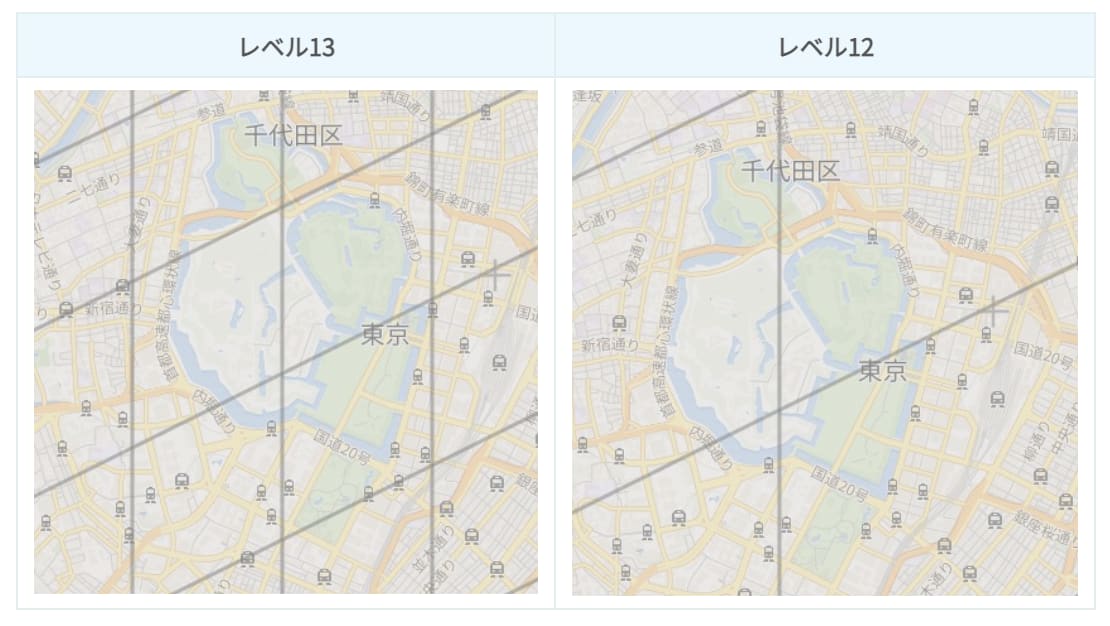
- S2セルにはレベルという概念があります。
- S2セルのレベルとは、レベルが大きいほど1つ1つのセルが細かくなります。
実現方法
RegionCoverer
- RegionCovererは、ある地図上に指定した図形に対して、その図形を確実に埋めるセルのリストを返すものです。
- また、特定の位置の緯度/経度から、上記に記載したある指定した半径の円を図形とし利用することができます。 => これがミソです。
type RegionCoverer struct {
MinLevel int // 使用する最小セルレベル。
MaxLevel int // 使用される最大セルレベル。
LevelMod int // 使用するLevelMod。=> 指定しなくていいかもしれません。というより何を指しているのか今一つ分かりませんでした。
MaxCells int // 必要なセルの最大数。
}
- ライブラリのドキュメントを見ると、使用例が以下のようになっています。
注目部分が**「r := s2.Region(CapFromCenterArea(center, area))」**
ここで、特定の位置を生成していることがわかります。
今回の場合ですと、初めに載せた記事のやり方と類似するはずなので、CapFromCenterAngleというfucを使用します。
rc := &s2.RegionCoverer{MaxLevel: 30, MaxCells: 5}
r := s2.Region(CapFromCenterArea(center, area))
covering := rc.Covering(r)
- 下記はRegionCoverを可視化し、わかりやすくしたツールです。参考
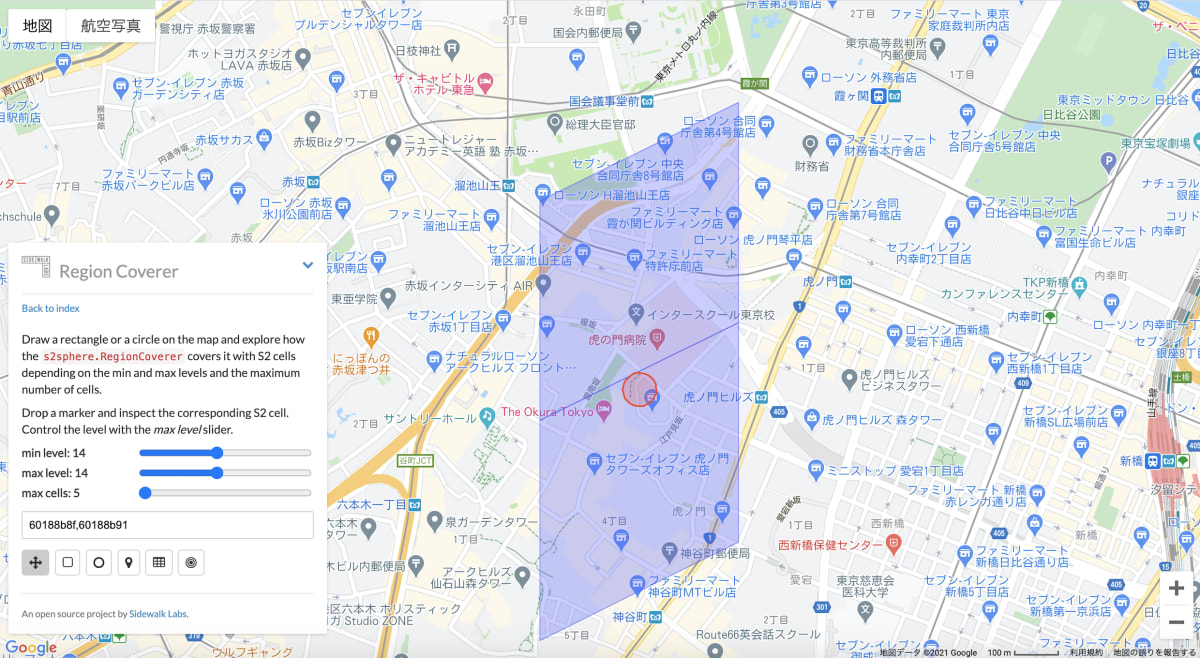
緯度/経度からある半径の円を生成する方法
LatLngFromDegrees
- S2 Geometryでは、緯度経度をLatLngという1対の角度として表します。
- そのため、LatLngFromDegreesというfuncを使用し、緯度/経度の情報を1対の角度に変換します。参考
type LatLng struct {
Lat, Lng s1.Angle
}
PointFromLatLng
- 後に出てくる、CapFromCenterAngleというfuncの引数に、LatLngではダメで、ポイントと呼ばれる値を引数で渡さないといけない。
- PointFromLatLngは、指定されたLatLngのポイントを返します。参考
CapFromCenterAngle
- CapFromCenterAngleは、指定されたポイントと角度でキャップを作成します。参考
func CapFromCenterAngle(center Point, angle s1.Angle) Cap
- angleという引数なのですがこれは、キャップの頂点となる球面上の点と、キャップの縁の大円に対する比率です。
- ユースケースとして「渋谷駅を中心に半径4kmの円」を想定した場合には、 地球のサイズの球からの相対的な比率計算をする必要があります。
- ここで、仮に地球の半径を6371.01kmと置くと、半径4kmの円の比率は4/6371.0となります。
- そのため、地球上の円を作成するためには以下のようにする必要があります。
const earthRadius float64 = 6371.01
capOnEarth := s2.CapFromCenterAngle(center, s1.Angle(4/earthRadius))
キャップとは何か
S2で扱う円は、平面上の円とは違い、球の表面に沿って曲ったキャップのような形状になっています。
そのため、S2では円はCapという型名です。
Discussion