PyMC:重回帰を題材にしたPyMCの紹介
はじめに
今回は重回帰を題材として私がStanやNumPyroと比べても便利だと感じた点を中心にPyMCの様々な機能を紹介していきます。
ライブラリのインポート
import os
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
import arviz as az
import pymc as pm
import pytensor.tensor as pt
# Initialize random number generator
RANDOM_SEED = 8927
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")
データの準備
アヒル本の5章のデータを使用して解析します。
df = pd.read_csv("../input/RStanBook/chap05/input/data-attendance-1.txt")
sns.pairplot(df, hue="A")
df["Score"] = df.Score.values/200.
df_X = df[["A", "Score"]]
df_y = df["Y"]

モデルの定義
PyMCでモデルを定義する場合は、with pm.Model() as model:のようにコンテキスト内でコードを記述します。ここではas modelとしていて、今後このモデルを使用したい場合は、with model:としたコンテキスト内で推論などのコードを実行することができます。
今回は説明変数が2変数なので、pm.Normal("slope", mu=0, sigma=20, shape=(n_var,))のようにbatch dimensionsを2に指定しています。また、途中で平均muを計算したデータを出力に保存したいため、pm.Deterministic()を使用しています。この関数はNumPyroの時と同様に単に出力にデータを保存しているだけです。最後に、likelihoodを計算するために、観察データをobserved=df_yという形で指定しています。
with pm.Model() as model:
# settings
n_var = df_X.shape[1]
# define prior
sigma = pm.HalfCauchy("sigma", beta=10)
intercept = pm.Normal("intercept", mu=0, sigma=20)
slope = pm.Normal("slope", mu=0, sigma=20, shape=(n_var,))
# calc mu
mu = pm.Deterministic("mu", intercept + pt.dot(df_X, slope))
# likelihood
likelihood = pm.Normal("likelihood", mu=mu, sigma=sigma, observed=df_y)
ここで、上記のコードが思い通りのコードになっているのかモデルを描画して確認してみます。ちゃんと重回帰が実装できていることが確認できます。
pm.model_to_graphviz(model)

しかし、上記の描画内容では入力データなどが省略されているので、より詳細に描画するためにモデルのコードを一部変更します。
PPLのコードを書く際に各分布の次元が何を表しているのか非常に分かりづらくなります。そのため、PyMCではcoordという機能を使用することで、次元に名前をつけることができます。例えば以下の例では、dataという名前に入力データXのデータ数(df_X.index)を、varという名前に入力データの次元数(df_X.columns)を割り当てています。この割り当てた名前を使用することで、dims="var"のように分布の形状を指定することができます(これはshape=(len(df_X.columns),)と同じ)。今回の例では変数の数が少ないため、ありがたみが少ないですが、複雑なモデルになるほどモデルの間違いを防ぐことができます。
また、入力自体もX = pm.Data("X", df_X, dims=('data', 'var'), mutable=True)のようにすることで明示的にモデルに組み込むことができます。これにより、モデルを描画する際にXやYも一緒に描画されることになります。
with pm.Model() as model:
# coords
model.add_coord('data', df_X.index, mutable=True)
model.add_coord('var', df_X.columns, mutable=True)
# data
X = pm.Data("X", df_X, dims=('data', 'var'), mutable=True)
y = pm.Data("y", df_y, dims=('data',), mutable=True)
# define prior
sigma = pm.HalfCauchy("sigma", beta=10)
intercept = pm.Normal("intercept", mu=0, sigma=20)
slope = pm.Normal("slope", mu=0, sigma=20, dims="var")
# calc mu
mu = pm.Deterministic("mu", intercept + pt.dot(X, slope), dims=('data',))
# likelihood
likelihood = pm.Normal("likelihood", mu=mu, sigma=sigma, observed=y, dims=('data',))
先ほどの図とは異なり、XやYとプレート上の数字が何を表しているのかが変数名が表示されることにより、モデルの詳細がよりわかりやすくなったかと思います。
pm.model_to_graphviz(model)

事前分布からのサンプリング
事前分布の妥当性を確認するために事前分布を用いてサンプリングしてみます。上記で作成したモデルを使用したい場合は、with model:としたコンテキスト内でコードを記述します。
with model:
idata = pm.sample_prior_predictive(samples=50, random_seed=rng)
Arvizで可視化してみます。実際のデータが0付近に集まっているのですが、事前分布からサンプリングした値は100あたりの値があり明らかに広げすぎていることがわかります。
az.plot_ppc(idata, num_pp_samples=50, group="prior");

上記の結果を踏まえて事前分布の値を少し変更してもう一度確認してみます。この結果、まだ観察データと比較すると大きすぎる気もしますが、ある程度適切そうな値が設定できたようにも見えルので、今回はこの計算条件で事後分布を推定したいと思います。
with pm.Model() as model:
# coords
model.add_coord('data', df_X.index, mutable = True)
model.add_coord('var', df_X.columns, mutable = True)
# data
X = pm.Data("X", df_X, dims=('data', 'var'), mutable=True)
y = pm.Data("y", df_y, dims=('data',), mutable=True)
# define prior
sigma = pm.HalfCauchy("sigma", beta=1)
intercept = pm.Normal("intercept", mu=0, sigma=1)
slope = pm.Normal("slope", mu=0, sigma=1, dims="var")
# calc mu
mu = pm.Deterministic("mu", intercept + pt.dot(X, slope), dims=('data',))
# likelihood
likelihood = pm.Normal("likelihood", mu=mu, sigma=sigma, observed=y, dims=('data',))
with model:
idata = pm.sample_prior_predictive(samples=100, random_seed=rng)
az.plot_ppc(idata, num_pp_samples=100, group="prior");

MCMC
以下のコードでMCMCを実行できます。複数のモデルを比較したい際にWAICなどを計算する際に対数尤度使用するので、idata_kwargs={"log_likelihood": True}を引数に加えることで、対数尤度を計算した値もidata内に出力しておきます。
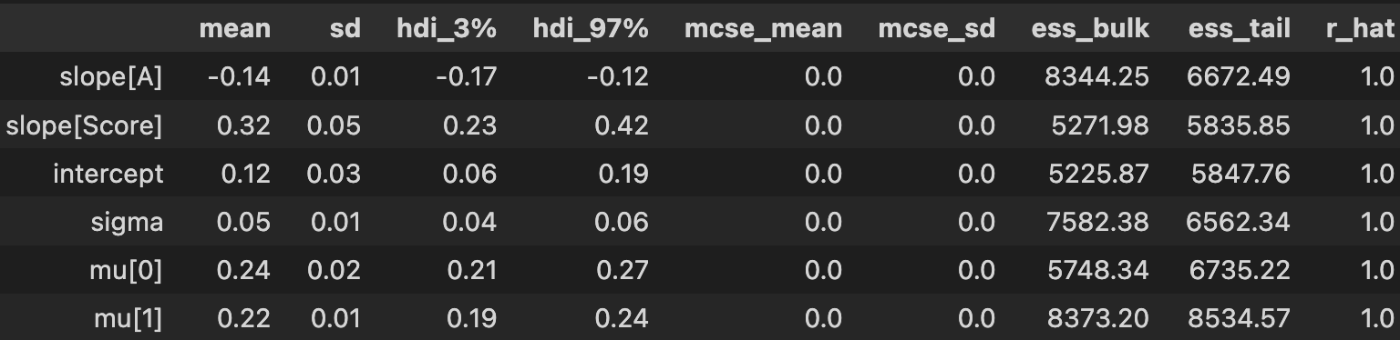
Summary内のSlopeを見るとslope[A], slope[Score]と表示されています。これはモデルを定義した際にmodel.add_coord('var', df_X.columns, mutable = True)としたためで、非常に人間に優しい表示になっています。
with model:
idata = pm.sample(3000,
tune=1000,
chains=4,
idata_kwargs={"log_likelihood": True},
random_seed=42,
target_accept=0.90,
return_inferencedata=True)
az.summary(idata, round_to=2)

NumPyroサンプラー
上記のデフォルトのコードのままでは今回のような単純なモデルでも少し時間がかかっているかと思います。そこで、PyMCではバックエンドでNumPyroで実行するオプションをつけることで、爆速になります。コードとしては上記のコードにnuts_sampler="numpyro",引数を追加するだけです。素晴らしいですね!NumPyroの時もそうでしたが、実行時間はStanと同程度ですが、Stanで時間がかかるコンパイル時間が短いので、体感はStanよりかなり速く感じます。
with model:
idata = pm.sample(3000,
tune=1000,
nuts_sampler="numpyro",
chains=4,
idata_kwargs={"log_likelihood": True},
random_seed=42,
target_accept=0.90,
return_inferencedata=True)
az.summary(idata, round_to=2)
可視化
arvizを使用してモデルが収束しているか確認していきます。
トレースプロット
各分布は歪な形をしてないですし、chain間の比較をしてもしっかり収束していそうです。
az.plot_trace(idata, combined=True, var_names=["intercept", "sigma", "slope"]);

Energyプロット
energy plotを可視化します。Marginal EnergyとEnergy Transitionの分布はある程度一致しており、サンプリングはうまくいっていそうです。
az.plot_energy(idata);

事後分布の確認
各変数の事後分布を可視化します。
az.plot_posterior(idata, var_names=["intercept", "slope"]);

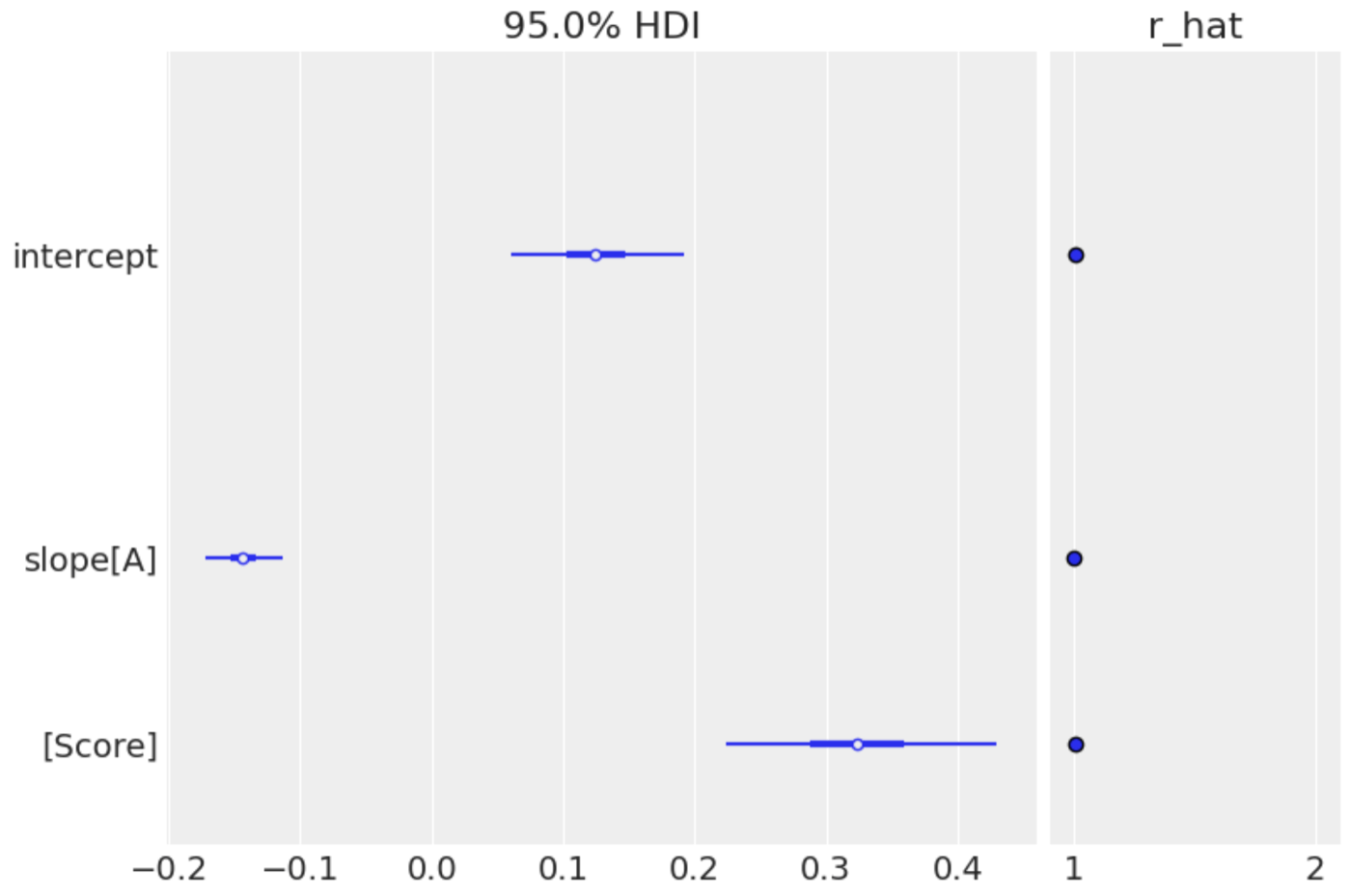
forest plotでRハットと一緒に可視化してみます。Rハットも1で収束に問題はないです。
az.plot_forest(idata, var_names=["intercept", "slope"], combined=True, hdi_prob=0.95, r_hat=True);
予測
上記のように取得できる事後分布の情報を使用して自分で計算してもいいですが、PyMCでは便利関数が用意されているので使っていきます。coordの情報が訓練データのままになっているので、pm.set_dataで検証用データの情報に更新した後に、pm.sample_posterior_predictive()関数で予測を行います。
X_new = df_X.tail()
with model:
pm.set_data({"X": X_new, 'y': np.zeros(len(X_new))}, coords={"data": X_new.index})
idata.extend(pm.sample_posterior_predictive(idata))
idata
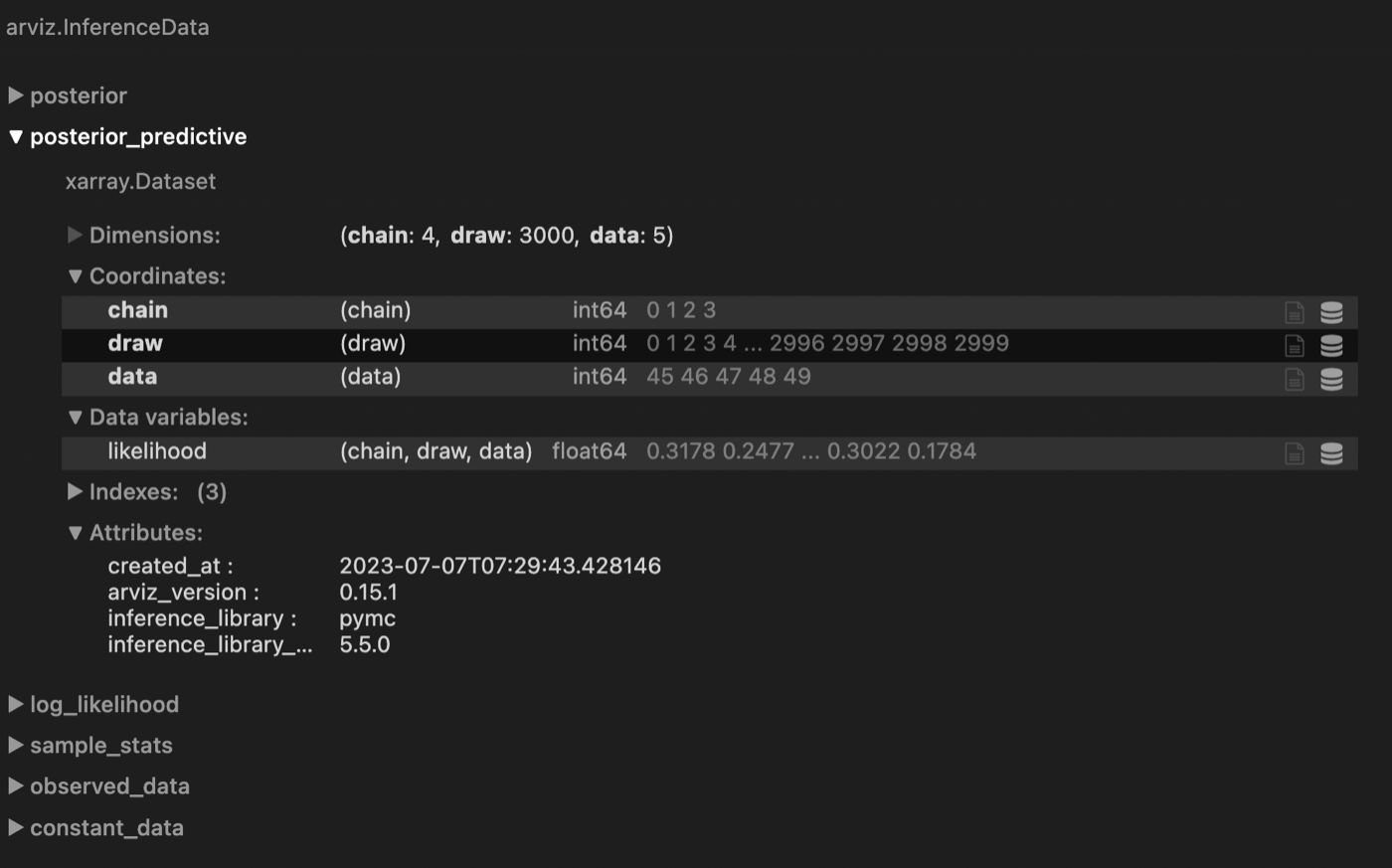
上記を実行すると、idataにposterior_predictiveが追加されます。
idata.posterior_predictive["likelihood"].mean(dim=["draw", "chain"])

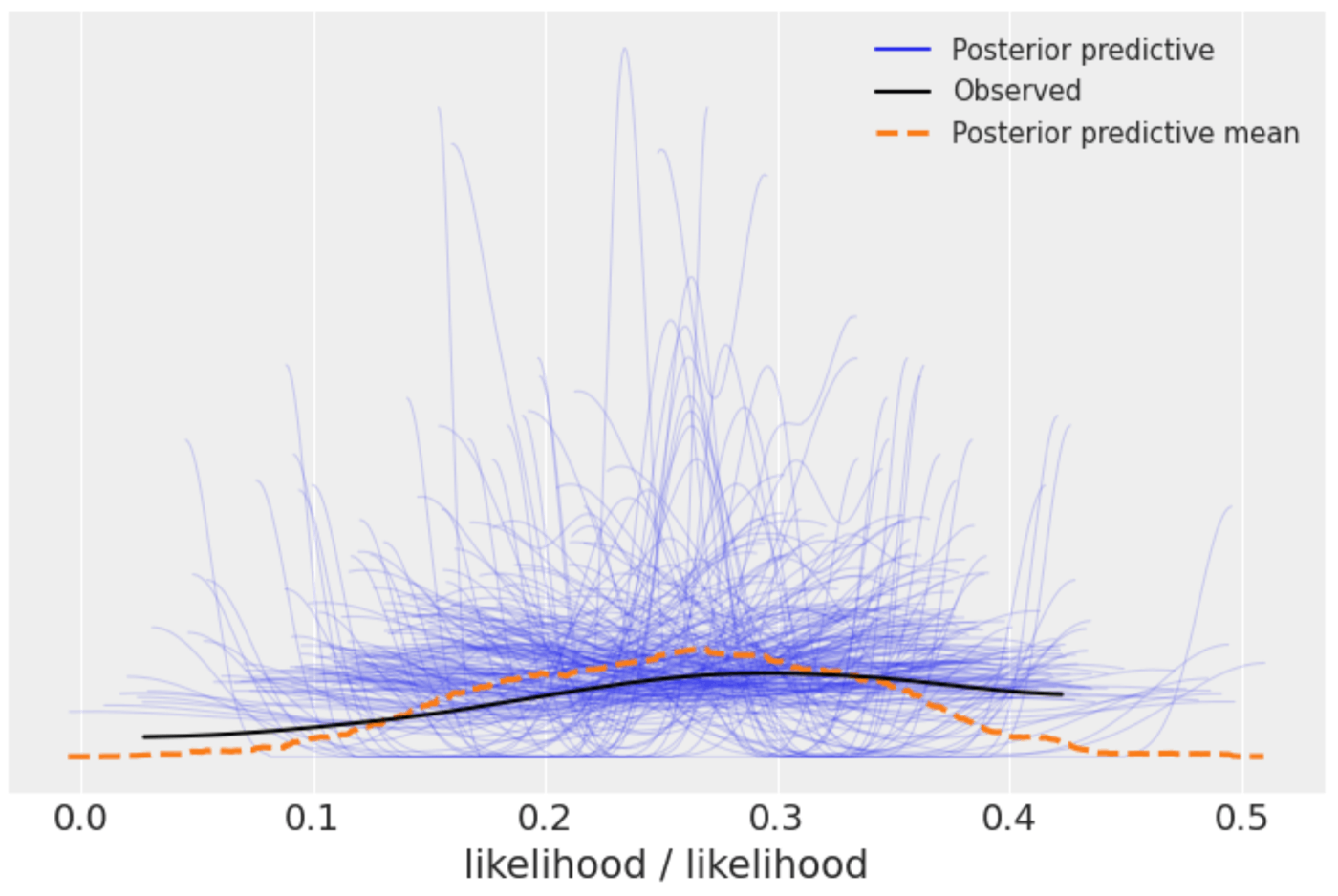
事前分布の時と同様に、likelihoodの事後分布も可視化してみます。事後分布は実測の黒線と大体被っておりうまく予測もできてそうです。
az.plot_ppc(idata, num_pp_samples=200);
デプロイ用クラス
ベイズはモデルの拡張性が高いことが長所ですが、高すぎるゆえにscikit-learnのような決まった型がない(機能が標準化されていない)ことが欠点でした。そこで、PyMCではModelBuilderクラスを使用することで、型を提供し柔軟なモデルの拡張と利便性を両立しています。
モデルの定義
まだ実験的な要素なので、add_coordを入れようと思うとメソッドを上書きするなど対応が必要でした。少しめんどくさいですが、FitやPredictのようにインターフェイスを簡略化できるのはいいですね。
import pandas as pd
from typing import Dict, Union
import xarray as xr
from pymc_experimental.model_builder import ModelBuilder
class LinearRegression(ModelBuilder):
# model name
_model_type = "LinearRegression"
# version
version = "0.1"
def build_model(self, X: pd.DataFrame, y: pd.Series) -> None:
""" create the PyMC model
Args:
X (pd.DataFrame): X
y (pd.Series): y
model_config (Dict[str, float], optional): パラメータが格納された辞書. Defaults to None.
"""
with pm.Model() as model:
# add coord
model.add_coord('data', X.index, mutable=True)
model.add_coord('var', X.columns, mutable=True)
# create data containers
x_data = pm.Data("x_data", X.values, dims=('data', 'var'), mutable=True)
y_data = pm.Data("y_data", y.values, dims=('data',), mutable=True)
# prior parameters
slope_mu_prior = self.model_config.get("slope_mu_prior", 0)
slope_sigma_prior = self.model_config.get("slope_sigma_prior", 1)
intercept_mu_prior = self.model_config.get("intercept_mu_prior", 0)
intercept_sigma_prior = self.model_config.get("intercept_sigma_prior", 1)
sigma_beta_prior = self.model_config.get("sigma_beta_prior", 1)
# define prior
slope = pm.Normal("slope", mu=slope_mu_prior, sigma=slope_sigma_prior, dims=("var",))
intercept = pm.Normal("intercept", mu=intercept_mu_prior, sigma=intercept_sigma_prior)
sigma = pm.HalfCauchy("sigma", beta=sigma_beta_prior)
# calc mu
mu = pm.Deterministic("mu", intercept + pt.dot(x_data, slope), dims=('data',))
# likelihood
obs = pm.Normal("y", mu=mu, sigma=sigma, observed=y_data, dims=(('data',)))
self.model = model
def generate_and_preprocess_model_data(self, X: pd.DataFrame, y: pd.Series) -> None:
""" Applies preprocessing to the data before fitting the model.
"""
self.X = X
self.y = pd.Series(y)
@property
def output_var(self) -> str:
""" Returns the name of the output variable of the model.
"""
return 'y'
def _data_setter(self, X: pd.DataFrame, y: pd.Series=None):
""" works as a set_data for the model and updates the data whenever we need to.
Args:
X (pd.DataFrame): X
y (pd.Series): y
"""
with self.model:
pm.set_data(
{
"x_data": X.values,
"y_data": y.values if y is not None else np.zeros(len(X_new))
},
coords={"data": X.index}
)
@property
def default_sampler_config(self) -> Dict:
return {
"draws": 3000,
"tune": 1000,
"chains": 4,
"target_accept": 0.90,
"random_seed": 42,
"return_inferencedata": True,
"nuts_sampler": "numpyro",
"idata_kwargs": {"log_likelihood": True}
}
@property
def default_model_config(self) -> Dict:
return {
"slope_mu_prior": 0,
"slope_sigma_prior": 1,
"intercept_mu_prior": 0,
"intercept_sigma_prior": 1,
"sigma_beta_prior": 1
}
def predict_posterior(
self,
X_pred: Union[np.ndarray, pd.DataFrame, pd.Series],
extend_idata: bool = True,
combined: bool = True,
**kwargs,
) -> xr.DataArray:
"""
Generate posterior predictive samples on unseen data.
Parameters
---------
X_pred : array-like if sklearn is available, otherwise array, shape (n_pred, n_features)
The input data used for prediction.
extend_idata : Boolean determining whether the predictions should be added to inference data object.
Defaults to True.
combined: Combine chain and draw dims into sample. Won't work if a dim named sample already exists.
Defaults to True.
**kwargs: Additional arguments to pass to pymc.sample_posterior_predictive
Returns
-------
y_pred : DataArray, shape (n_pred, chains * draws) if combined is True, otherwise (chains, draws, n_pred)
Posterior predictive samples for each input X_pred
"""
X_pred_copy = X_pred.copy()
X_pred = self._validate_data(X_pred)
# model内部でDataFrameの情報を使用したいのでデータフレームに戻す
X_pred = pd.DataFrame(X_pred, index=X_pred_copy.index, columns=X_pred_copy.columns)
posterior_predictive_samples = self.sample_posterior_predictive(
X_pred, extend_idata, combined, **kwargs
)
if self.output_var not in posterior_predictive_samples:
raise KeyError(
f"Output variable {self.output_var} not found in posterior predictive samples."
)
return posterior_predictive_samples[self.output_var]
Fit
model = LinearRegression()
idata = model.fit(df_X, df_y)
az.summary(idata, round_to=2)
predict
pred_samples = model.predict_posterior(X_new)
pred_mean = model.predict(X_new)
save & load
model.save(f"{model._model_type}_{model.version}.nc")
model = model.load(f"{model._model_type}_{model.version}.nc")
最後に
以上で重回帰を題材にしたPyMCの紹介は終わりです。NumPyroの長所である速度を取り入れながら、PyMCの利便性を享受できるので、個人的には非常に気に入っています。
また、coordやpm.Dataなども痒いところに手が届く機能になっており、ベイズのコーディング時の複雑さが軽減されているようにも思えます。
Discussion