📖
PyMC:階層モデルとモデルの比較
はじめに
今回は階層モデルとモデルの比較方法についてみていきます。
ライブラリのインポート
import os
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
import arviz as az
import pymc as pm
import pytensor.tensor as pt
# Initialize random number generator
RANDOM_SEED = 8927
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")
データの準備
アヒル本8章のデータを使用します。
df = pd.read_csv("../input/RStanBook/chap08/input/data-salary-2.txt")
df["KID"] = df["KID"] -1
df.head()
df_X = df["X"]
df_y = df["Y"]
KID = df["KID"].values
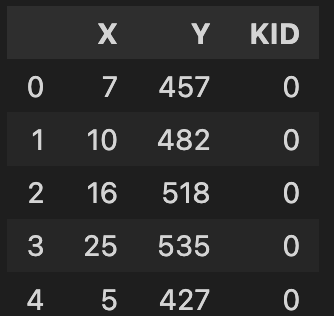
モデルの定義
階層なし
比較用に単純な階層なしの回帰モデルを構築します。
with pm.Model() as model_normal:
# coords
model_normal.add_coord('data', df_X.index, mutable=True)
# data
X = pm.Data("X", df_X.values, dims=('data'), mutable=True)
y = pm.Data("y", df_y, dims=('data',), mutable=True)
# prior
intercept = pm.Normal("intercept", mu=0, sigma=100)
coef = pm.Normal("coef", mu=0, sigma=100)
sigma_Y = pm.HalfNormal("sigma_Y", sigma=100)
# calc mu
mu = pm.Deterministic("mu", intercept + pt.dot(X, coef), dims=('data',))
# likelihood
obs = pm.Normal("obs", mu=mu, sigma=sigma_Y, observed=y, dims=('data',))
pm.model_to_graphviz(model_normal)

階層モデル
KIDのグループごとに係数と切片を推論します。ここで、KIDの数だけdims=('n_k',)で次元を指定しています。
with pm.Model() as model_hierarchical:
# coords
model_hierarchical.add_coord('data', df_X.index, mutable=True)
model_hierarchical.add_coord('n_k', np.unique(KID), mutable=True)
# data
X = pm.Data("X", df_X.values, dims=('data',), mutable=True)
y = pm.Data("y", df_y, dims=('data',), mutable=True)
kid = pm.Data("kid", KID, dims=('data',), mutable=True)
# prior
intercept_mu_common = pm.Normal("intercept_mu_common", mu=0, sigma=100)
intercept_sigma_common = pm.HalfNormal("intercept_sigma_common", sigma=100)
coef_mu_common = pm.Normal("coef_mu_common", mu=0, sigma=100)
coef_sigma_common = pm.HalfNormal("coef_sigma_common", sigma=100)
sigma_Y = pm.HalfNormal("sigma_Y", sigma=100)
# kidごと
coef = pm.Normal("coef", mu=coef_mu_common, sigma=coef_sigma_common, dims=('n_k',))
intercept = pm.Normal("intercept", mu=intercept_mu_common, sigma=intercept_sigma_common, dims=('n_k',))
# calc mu
mu = pm.Deterministic("mu", intercept[kid] + coef[kid]*X, dims=('data',))
# likelihood
obs = pm.Normal("obs", mu=mu, sigma=sigma_Y, observed=y, dims=('data',))
pm.model_to_graphviz(model_hierarchical)

MCMC
with model_normal:
idata_normal = pm.sample(3000,
tune=3000,
nuts_sampler="numpyro",
chains=4,
idata_kwargs={"log_likelihood": True},
random_seed=42,
target_accept=0.90,
return_inferencedata=True)
az.summary(idata_normal, round_to=2)

with model_hierarchical:
idata_hierarchical = pm.sample(3000,
tune=3000,
nuts_sampler="numpyro",
chains=4,
idata_kwargs={"log_likelihood": True},
random_seed=42,
target_accept=0.99,
return_inferencedata=True)
az.summary(idata_hierarchical, round_to=2)

可視化
収束性を確認します。階層モデルの方は収束はしていますが、発散しているサンプルがいくつかあるようです。
az.plot_trace(idata_normal);

az.plot_trace(idata_hierarchical);

モデルの比較
今回はLOO(Leave-one-out cross-validation)とWAIC(the widely applicable information criterion )でモデルの比較を行います。LOOとWAICともにパラメータ値の事後シミュレーションで評価される対数尤度を用いて、汎化誤差を近似して求める手法になります。MCMCの計算する結果を用いて計算できるため、モデルを何回もフィットさせる必要がありません。
LOO
表の項目はそれぞれ以下を表します。今回はWarningが出ていますが、、、階層モデルの方が良さそうであることがわかります。また、LOOとWAICの結果を比較するとほとんど差がないことがわかります。
- rank : モデルのランキング(0が一番いいモデル)
- elpd_loo:looの値
- p_loo:ペナルティ項(雑には有効パラメータ数(汎関数分散)のような値)の値
- elpd_diff:一番いいモデルとの差
- weight : 各モデルに割り当てられた重み, 各モデルが正しい確率として解釈可能
- se : looの標準偏差
- dse : ??
- warning : 値の信頼性(今回は階層モデルで一部発散しているのでTrueになっている)
- scale : 表示されている値のスケール
df_comp_loo = az.compare({"hierarchical": idata_hierarchical, "normal": idata_normal})
df_comp_loo

az.plot_compare(df_comp_loo, insample_dev=False);

WAIC
df_comp_waic = az.compare({"hierarchical": idata_hierarchical, "normal": idata_normal}, ic="waic")
df_comp_waic

az.plot_compare(df_comp_waic, insample_dev=False);

最後に
今回は階層モデルとモデルの比較を紹介しました。Pythonでベクトルの扱いに慣れていれば自然に階層モデルを構築できそうです。また、Arvizによりモデルの比較を行うためのWAICやLOOの計算も簡単に実行できました。
Discussion