cmdstanpy : 単回帰
import os
import time
import pandas as pd
import matplotlib.pyplot as plt
from cmdstanpy import CmdStanModel
データの読み込み
以下のデータを使用しています。
df = pd.read_csv("./data-salary.txt")
plt.scatter(df["X"], df["Y"])
plt.xlabel("age")
plt.ylabel("salary [10^4 yen]")
plt.show()

モデル式
上記を見ると年齢と年収は線形に相関する年功序列の関係が強く現れていることがわかるので、線形の単回帰でモデル式を構築します。
output_dir = "./output/"
os.makedirs(output_dir, exist_ok=True)
stan_file = "./simpleLR.stan"
exe_file = "./simpleLR"
コンパイル
if not os.path.exists(exe_file):
model = CmdStanModel(stan_file=stan_file)
else:
model = CmdStanModel(exe_file=exe_file)
データ
data = {
"N": len(df),
"X": df["X"].values,
"Y": df["Y"].values,
}
print(data)
フィッティング
CmdStanPyでは以下のsample()メソッドにより、ハミルトンモンテカルロ(HMC)サンプリングを使って、データを条件としたモデルに対するベイズ推定を行います。このメソッドは、モデルとデータに対してStanのHMC-NUTSサンプラーを実行し、CmdStanMCMCオブジェクトを返します。
データは以下のようにPythonの辞書型でも渡せますし、ファイルパスを渡すこともできます。
import multiprocessing
num_cpu = multiprocessing.cpu_count()
fit = model.sample(
data=data,
chains=4, # chain数
seed=1, # seed固定
iter_warmup=1000, # warmupの数
iter_sampling=2000, # samplingの数
parallel_chains=num_cpu, # 並列数
save_warmup=True, # warmupもCSVに保存
thin=1, # サンプリング間隔
output_dir=output_dir, # 出力先
# show_console=True, # 標準出力
show_progress=True # progress出力
)
結果の確認
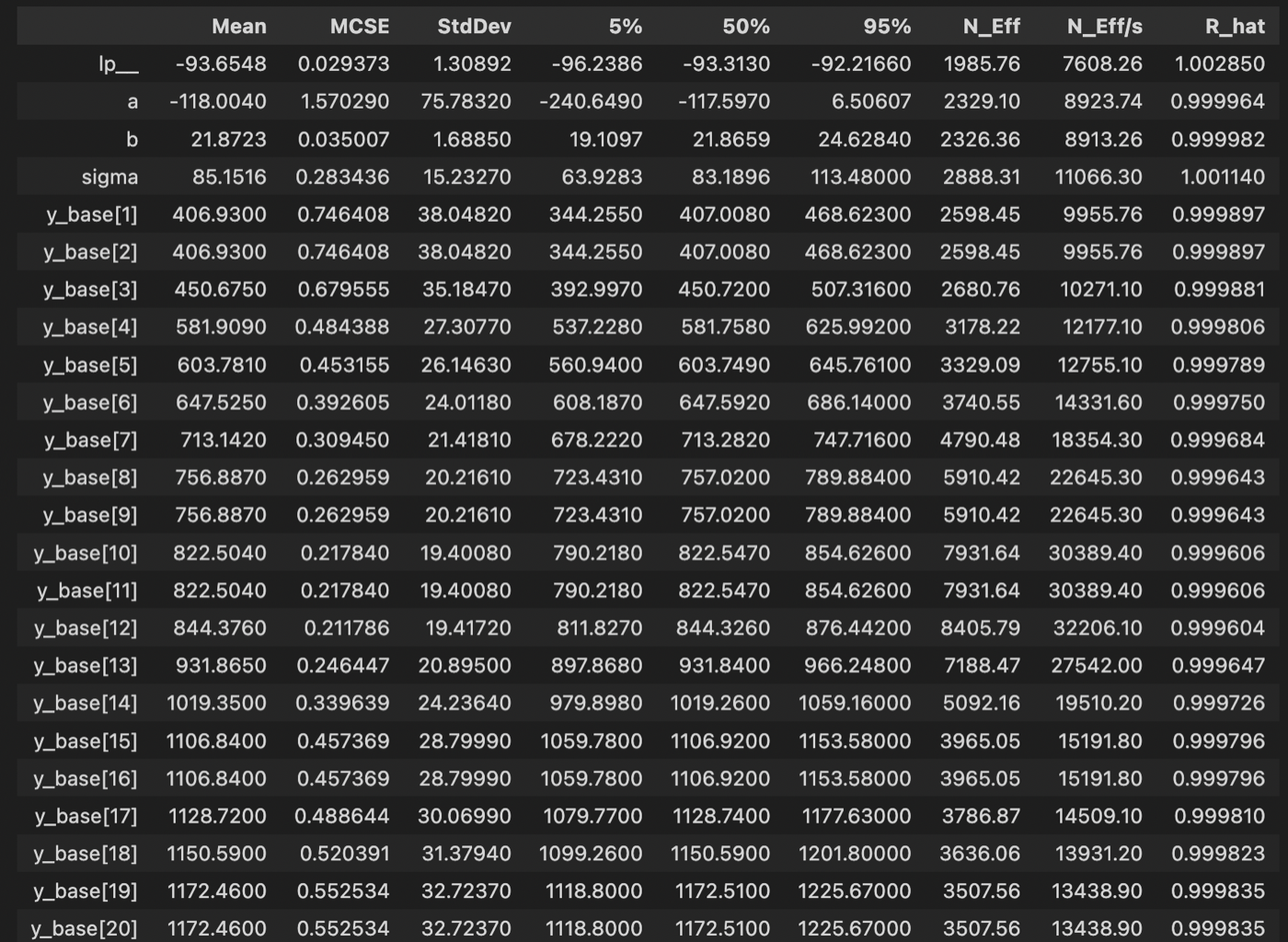
fit.summary()で各パラメータの要約が見られます。lp__は対数事後確率で他のパラメータ同様に収束する必要があります。
また、N_EffはStanが自己相関等から判断した実効的なMCMCサンプル数です。この数が少ないと収束しづらいパラメータであることが分かります。大体1000サンプルほどあると良いものです。
fit.summary()
arvizによる収束性判断
import numpy as np
import arviz as az
import xarray as xr
az.style.use("arviz-darkgrid")
cmdstanpyからarviz用のデータへ変換
cmdstanpy_data = az.from_cmdstanpy(
posterior=fit,
log_likelihood="lp__",
)
cmdstanpy_data
ll_data = cmdstanpy_data.log_likelihood
対数事後確率のプロット
az.plot_trace(ll_data, compact=False);

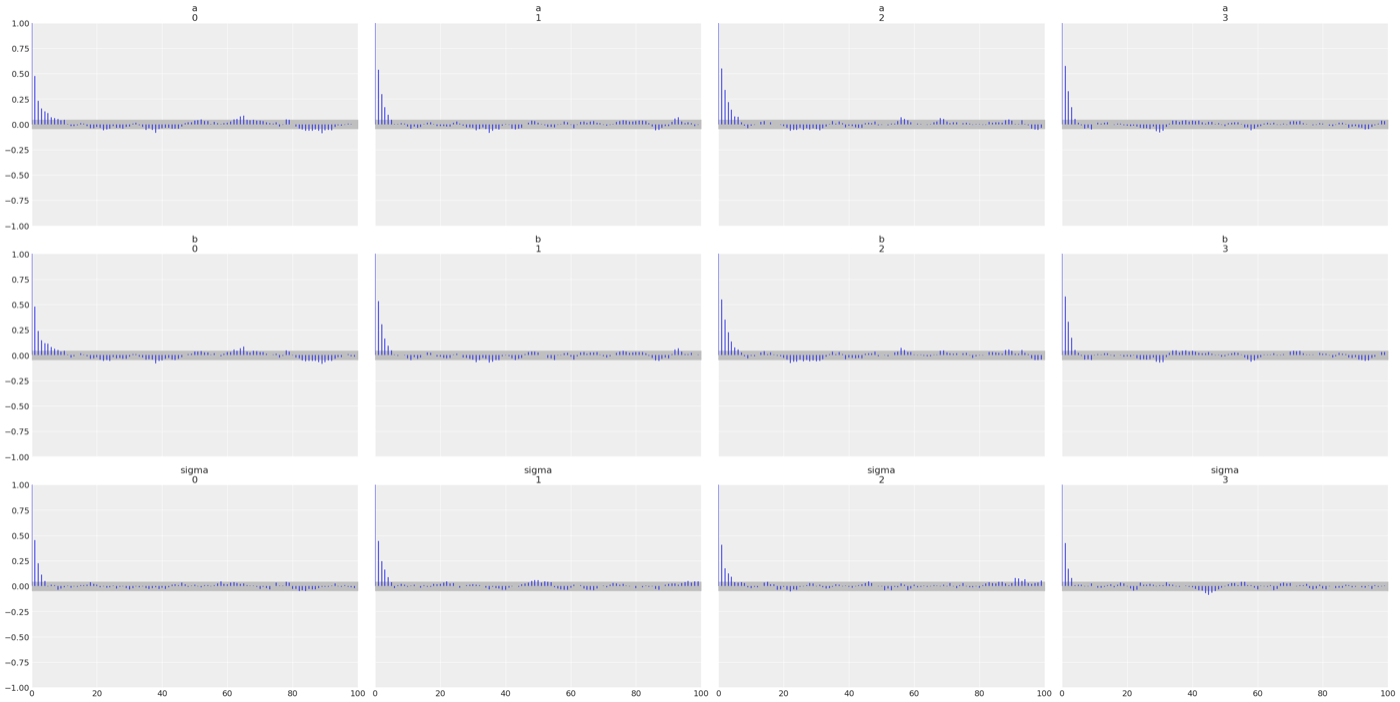
自己相関プロット
ほとんど自己相関がないことがわかる
az.plot_autocorr(cmdstanpy_data, grid=(3, 4), var_names=["a", "b", "sigma"]);
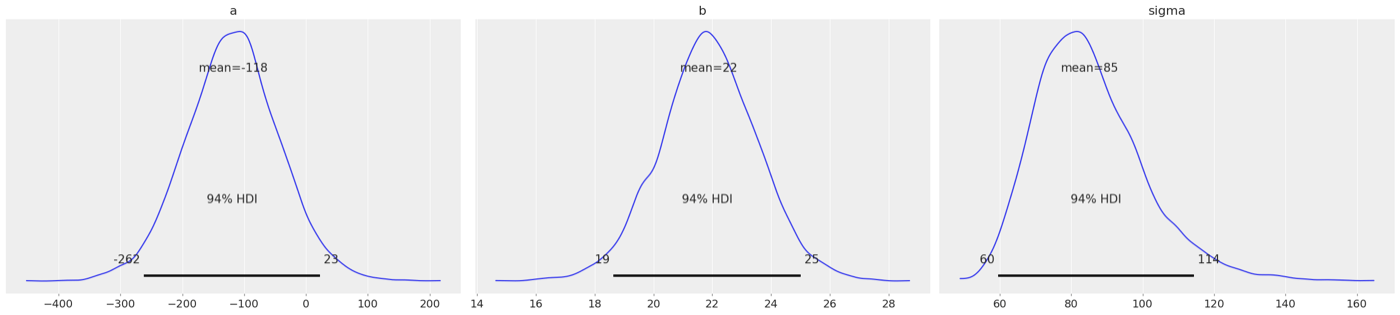
事後分布のプロット
az.plot_posterior(cmdstanpy_data, var_names=["a", "b", "sigma"]);
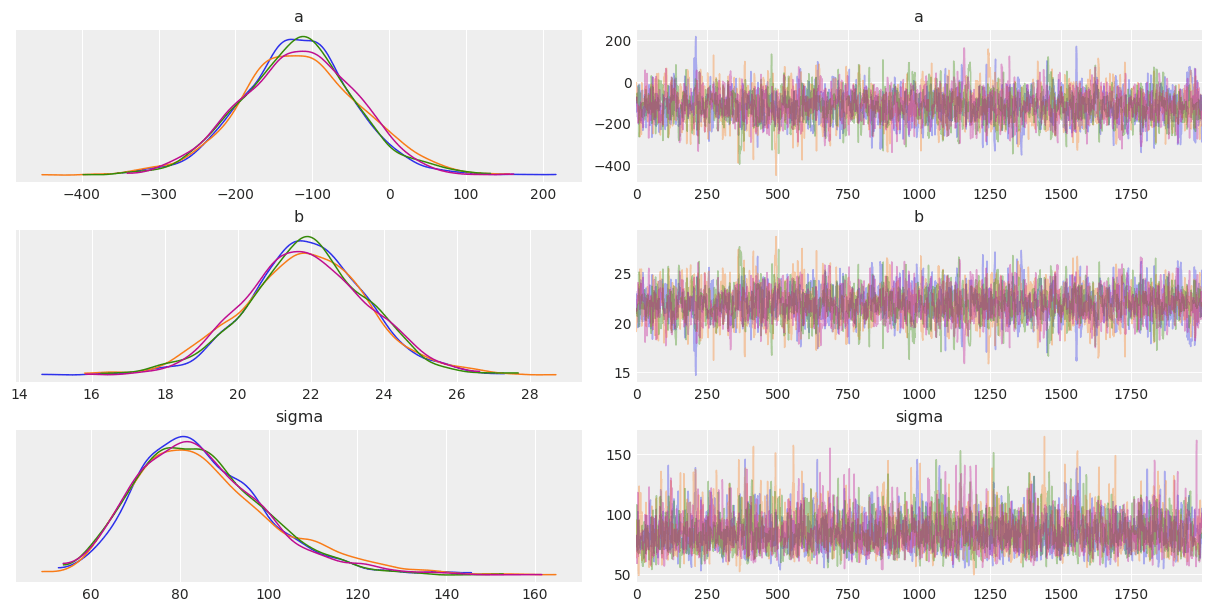
トレースプロット
ある点を中心にプロットされているので収束していることがわかる。
az.plot_trace(cmdstanpy_data, compact=False, var_names=["a", "b", "sigma"]);
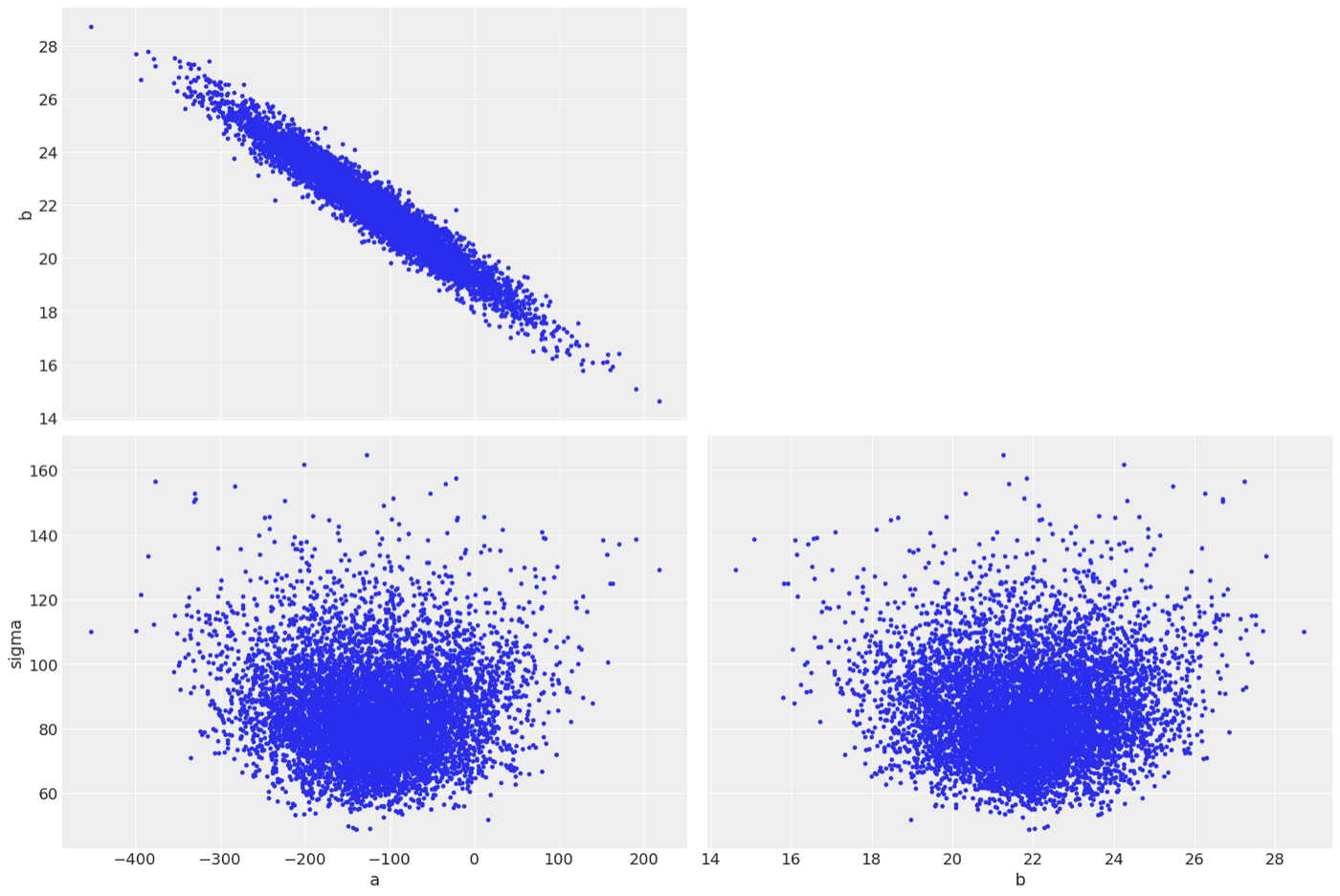
パラメータのペアプロット
aとbは負の相関があることがわかる。
az.plot_pair(
cmdstanpy_data,
divergences=True,
var_names=["a", "b", "sigma"]
);
ベイズ信頼区間とベイズ予測区間
generate_quantities blockを用いて、23~60歳までの基本年収のベイズ信頼区間と年収のベイズ予測区間を計算し可視化します。
generate_quantities blockはパラメータや定数から新たにサンプリングする変数を作ることができます。この時、事後確率からは切り離されているので計算が早いのが特徴です。
data = {
"N": len(df),
"X": df["X"].values,
"Y": df["Y"].values,
"N_new": len(list(range(23, 61))),
"X_new": list(range(23, 61))
}
print(data)
simpleLR.stanが無事に収束していることを確認した後に、generate_quantities blockが追加されたsimpleLR_ppc.stanをコンパイルし実行します。
ppc_model = CmdStanModel(stan_file='simpleLR_ppc.stan')
ppc_model.compile()
new_quantities = ppc_model.generate_quantities(data=data, mcmc_sample=fit, seed=1)
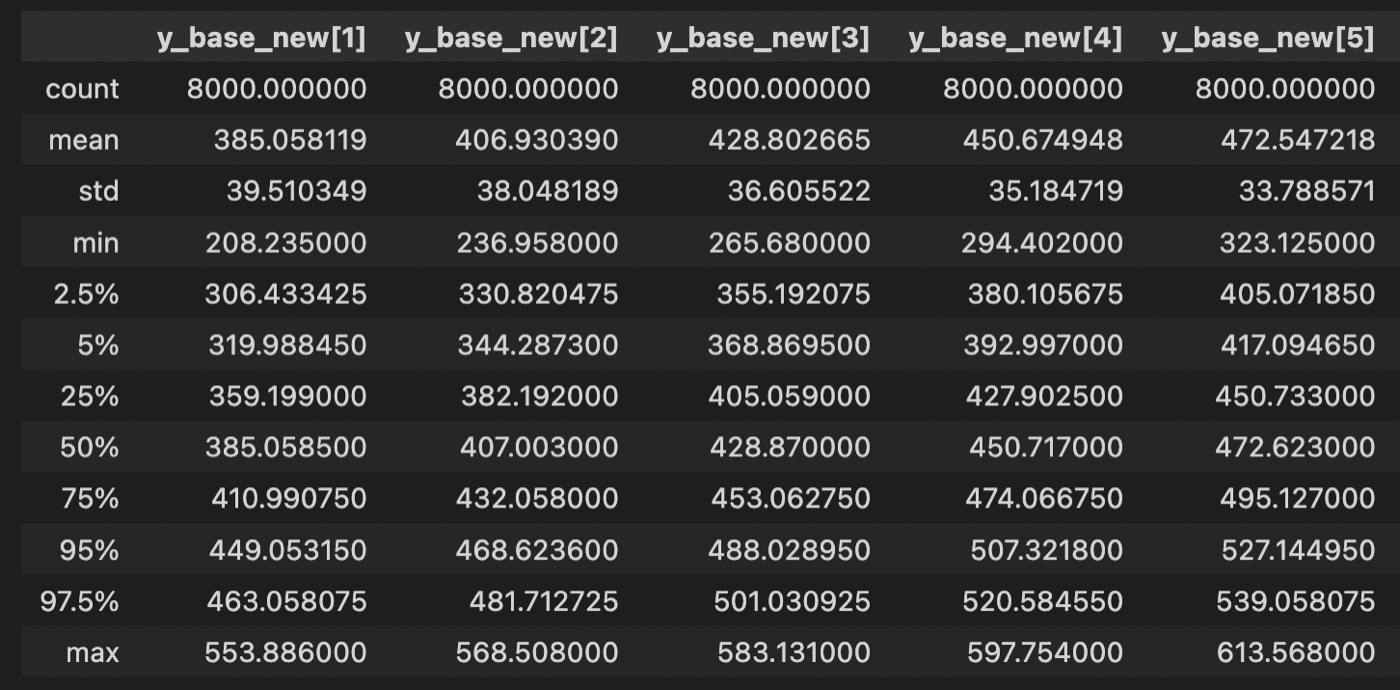
50%と95%信頼区間を計算しプロットします。
df_result = new_quantities.draws_pd().describe(percentiles=[.025, .05, .25, .5, .75, .95, .975])
df_result
df_base = df_result.loc[:, df_result.columns.str.contains("base")].T
df_base["age"] = list(range(23, 61))
df_base.head(3)
plt.figure(figsize=(4, 4))
plt.plot(df_base["age"], df_base["mean"], '-', linewidth=2)
plt.fill_between(df_base["age"], df_base["2.5%"], df_base["97.5%"], color='#888888', alpha=0.4)
plt.fill_between(df_base["age"], df_base["25%"], df_base["75%"], color='#222222', alpha=0.4)
plt.xlabel("age"); plt.ylabel("base salary")
plt.title("base salary")
plt.tight_layout()
plt.show()
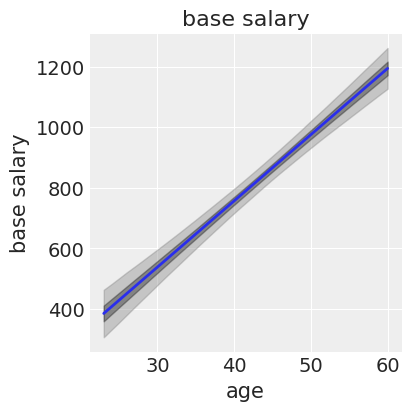
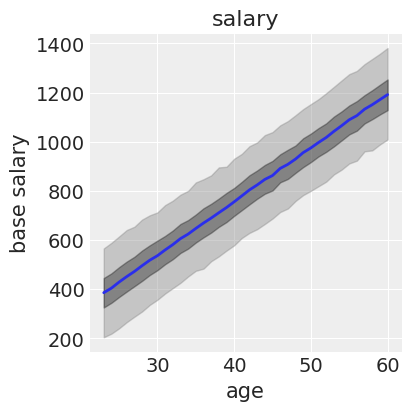
df_new = df_result.loc[:, df_result.columns.str.contains("y_new")].T
df_new["age"] = list(range(23, 61))
df_new.head(3)
plt.figure(figsize=(4, 4))
plt.plot(df_new["age"], df_new["mean"], '-', linewidth=2)
plt.fill_between(df_new["age"], df_new["2.5%"], df_new["97.5%"], color='#888888', alpha=0.4)
plt.fill_between(df_new["age"], df_new["25%"], df_new["75%"], color='#222222', alpha=0.4)
plt.xlabel("age"); plt.ylabel("base salary")
plt.title("salary")
plt.tight_layout()
plt.show()


Discussion