【C言語入門の次】 第11回 ヒープソート

https://youtu.be/57-qTYXcHb4

$\textcolor{pink}{四国めたん: }$教師役ですわ

$\textcolor{lime}{ずんだもん: }$生徒役なのだ

$\footnotesize \textcolor{pink}{四国めたん:}$ こんにちは。四国めたんです

$\footnotesize \textcolor{lime}{ずんだもん:}$ ずんだもんなのだ。こんにちはなのだ

$\footnotesize \textcolor{pink}{四国めたん:}$ 今回も ソート のアルゴリズムについてお話ししますわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ りょうかいなのだ

$\footnotesize \textcolor{pink}{四国めたん:}$ 今回は ヒープソート についてお話ししますわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ よろしくなのだ

ヒープソート

ヒープ

$\footnotesize \textcolor{lime}{ずんだもん:}$ ところで ヒープ とはなんなのだ

$\footnotesize \textcolor{pink}{四国めたん:}$ ヒープ とは、連結リスト等と同じく、データ構造の一種である ツリー構造 のひとつですわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ ツリー構造 ？

$\footnotesize \textcolor{pink}{四国めたん:}$ ツリー構造 というのは、一般的には木を逆さまにしたような見た目をしていますわ

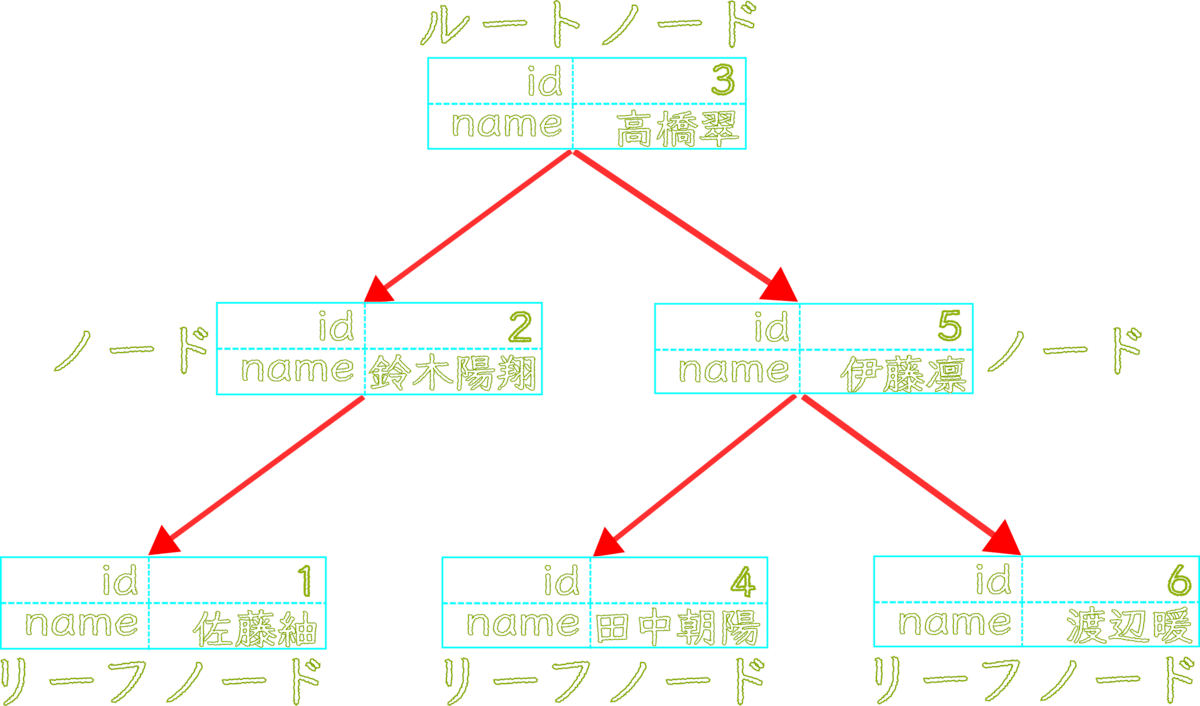
$\footnotesize \textcolor{lime}{ずんだもん:}$ なんか、どこかで見たような気がする...

$\footnotesize \textcolor{pink}{四国めたん:}$ はい、第4.5章 連結リストのバリエーションの 二分木 と同じですわね

$\footnotesize \textcolor{pink}{四国めたん:}$ おさらいすると、それぞれのデータは ノード とよばれ、その位置によって名前が付けられていますわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ ある ノード に対し、連結された ノード を 子ノード と呼ぶのだ

$\footnotesize \textcolor{pink}{四国めたん:}$ はい、逆に 子ノード から見て、連結元の ノード を 親ノード と呼びますわ

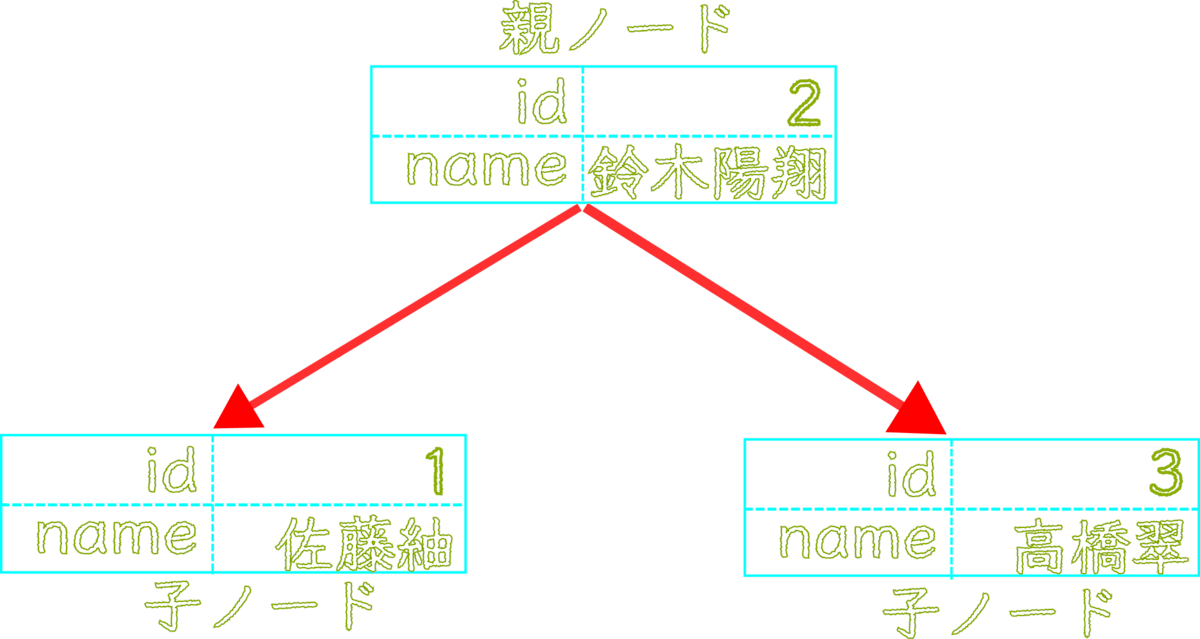
$\footnotesize \textcolor{lime}{ずんだもん:}$ 親ノード を持たない、一番上の ノード を ルートノード と云うのだ

$\footnotesize \textcolor{pink}{四国めたん:}$ そうですわね

$\footnotesize \textcolor{lime}{ずんだもん:}$ また、 子ノード を持たない、一番下の ノード を リーフノード と云うのだ

$\footnotesize \textcolor{pink}{四国めたん:}$ よく覚えていましたわね

$\footnotesize \textcolor{lime}{ずんだもん:}$ まかせるのだ

$\footnotesize \textcolor{pink}{四国めたん:}$ データ構造のイメージとしては、連結リストとおなじですわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ うむ

$\footnotesize \textcolor{pink}{四国めたん:}$ ただ、一般的な連結リストの連結先が1つなのに対して、 ツリー構造 は、連結先が複数だというところが異なっていますわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ 二本木 なら連結先が2つなのだ

$\footnotesize \textcolor{pink}{四国めたん:}$ はい、一般的には連結先が2つの 二分木 が ツリー構造 としては、よく使われますわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ なるほどなのだ

$\footnotesize \textcolor{pink}{四国めたん:}$ そして、 ヒープ というのは、特別な条件によってデータの並びを整えた ツリー構造 のことを指しますわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ 特別な条件とはなんなのだ？

$\footnotesize \textcolor{pink}{四国めたん:}$ 一般的に、ソートに使う ヒープ は、 親ノード のデータが 子ノード のデータよりも小さい、もしくは大きいという条件で並べますわ

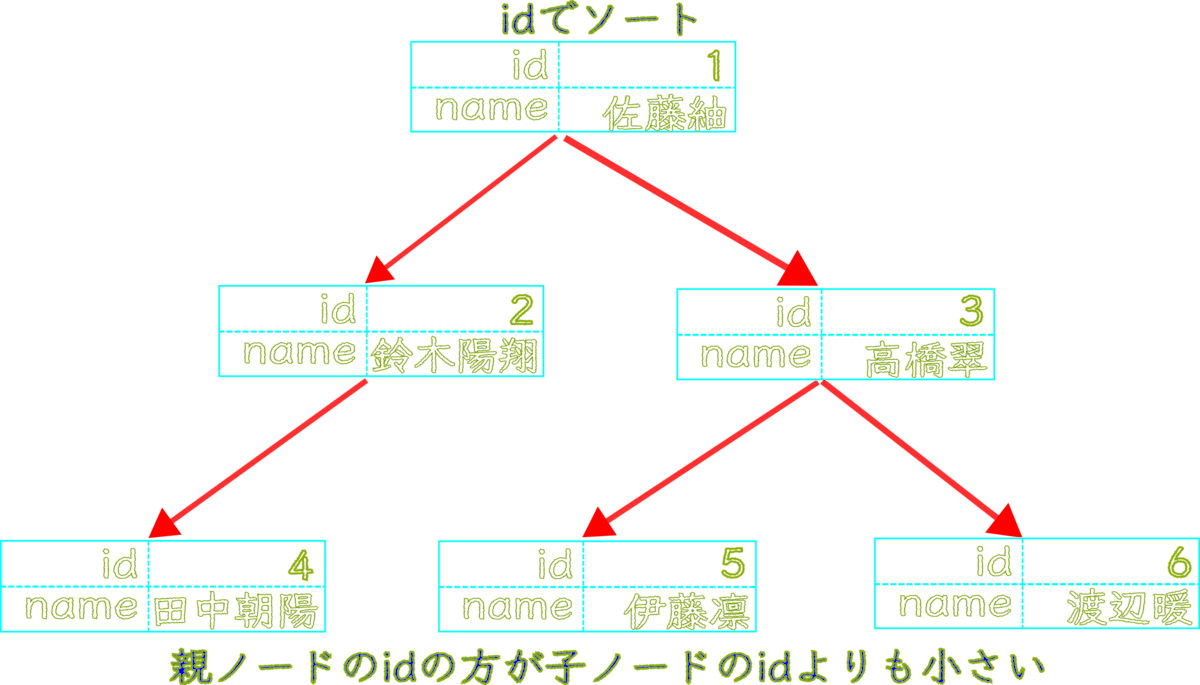
$\footnotesize \textcolor{lime}{ずんだもん:}$ つまり、 ルートノード のデータが一番大きい、もしくは一番小さい値となるのだ

$\footnotesize \textcolor{pink}{四国めたん:}$ そうですわね

ヒープソートの原理

$\footnotesize \textcolor{pink}{四国めたん:}$ 次は ヒープソート の原理についてですわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ ヒープ を使ってソートをおこなうのではないのか？

$\footnotesize \textcolor{pink}{四国めたん:}$ まぁ、その通りですわね

1. 与えられたデータでヒープを作成
2. ルートノードからデータを取り出し
3. 残りのデータで再度ヒープを作成
4. ルートノードから再度データを取り出し
5. これを繰り返してデータを順番に並べる

$\footnotesize \textcolor{pink}{四国めたん:}$ とりあえず、与えられたデータで ヒープ を作成しますわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ うむ

$\footnotesize \textcolor{pink}{四国めたん:}$ 作成された ヒープ の ルートノード は一番大きい、もしくは一番小さい値なので、取り出して置きますわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ ふむ

$\footnotesize \textcolor{pink}{四国めたん:}$ 再度、残りのデータで ヒープ を作成すると、その ルートノード は2番目に大きい、もしくは小さい値となりますわね

$\footnotesize \textcolor{lime}{ずんだもん:}$ そのとおりなのだ

$\footnotesize \textcolor{pink}{四国めたん:}$ ですので、その値を取りだして、一番大きい、もしくは小さい値の次に置きますわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ なるほど、これを繰り返すと、最終的にデータを順番に並べることができるのだ

$\footnotesize \textcolor{pink}{四国めたん:}$ とりあえず実例を見てみましょう

$\footnotesize \textcolor{lime}{ずんだもん:}$ りょうかいなのだ

$\footnotesize \textcolor{pink}{四国めたん:}$ 今回は、降順にデータを並べてみますわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ うむ

$\footnotesize \textcolor{pink}{四国めたん:}$ まず、初期のデータとして適当な整数の配列を考えますわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ ふむ

$\footnotesize \textcolor{pink}{四国めたん:}$ これを 二分木 にしますわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ 連結リスト に作り直すのか？

$\footnotesize \textcolor{pink}{四国めたん:}$ いいえ、今回は、各配列の要素が 二分木 のようになっていると想定しているだけですわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ つまり、実際にツリー状に配置するのではなく、ツリー状になっていると仮定していると云うことか？

$\footnotesize \textcolor{pink}{四国めたん:}$ そうですわね

$\footnotesize \textcolor{pink}{四国めたん:}$ なお、左側の色付きの部分の数値は、配列のインデックスとしますわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ りょうかいなのだ

$\footnotesize \textcolor{pink}{四国めたん:}$ そして、この 二分木 を ヒープ として整えますわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ どのようにするのだ？

$\footnotesize \textcolor{pink}{四国めたん:}$ まずは リーフノード に着目して、 親ノード が 子ノード よりも小さい場合には、値を交換しますわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ 値だけ交換して、配列のインデックス、つまりツリーの構造はそのままと云うことか...

$\footnotesize \textcolor{pink}{四国めたん:}$ 次に、同じレベルのツリーに着目しますわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ 同じレベルのツリーで 親ノード が 子ノード よりも小さい場合には、値を交換すると云うことか...

$\footnotesize \textcolor{pink}{四国めたん:}$ はい、最後に ルートノード のツリーに着目し、 ルートノード が 子ノード よりも小さい場合には、値を交換しますわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ この時点で 二分木 は ヒープ として整えられた状態なのだ

$\footnotesize \textcolor{pink}{四国めたん:}$ はい、 ルートノード には最大の値が配置されていますわね

$\footnotesize \textcolor{lime}{ずんだもん:}$ りょうかいなのだ

$\footnotesize \textcolor{pink}{四国めたん:}$ ここで、 ルートノード である配列のインデックス0と配列の最後の値を交換しておきますわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ うむ

$\footnotesize \textcolor{pink}{四国めたん:}$ 次に、配列の最後の値はソート済みとして除外し、その他の値について、再度 二分木 として ヒープ を作成しますわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ うむ

$\footnotesize \textcolor{pink}{四国めたん:}$ これを繰り返すと、最終的にソートが完了しますわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ なるほどなのだ

ヒープソートの実装

$\footnotesize \textcolor{pink}{四国めたん:}$ それでは ヒープソート について実装してみましょう

$\footnotesize \textcolor{lime}{ずんだもん:}$ よろしくなのだ

$\footnotesize \textcolor{pink}{四国めたん:}$ ヒープソート については、連結リストのような構造を使うと非常に判り易いと思いますわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ そうなのか？

$\footnotesize \textcolor{pink}{四国めたん:}$ 特にデータのサイズが大きい場合には、データをコピーする量が少なくなるため、連結リストのような構造が有利ですわね

$\footnotesize \textcolor{lime}{ずんだもん:}$ なるほどなのだ

$\footnotesize \textcolor{pink}{四国めたん:}$ ですが、今回は配列をそのまま使って ヒープソート をおこなってみますわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ うむ

ヒープ関数

$\footnotesize \textcolor{pink}{四国めたん:}$ まずは、配列を使って ヒープ を作成しますわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ ポインタを使わずに 二分木 を作る方法がわからないのだ

$\footnotesize \textcolor{pink}{四国めたん:}$ 着目点は配列のインデックスですわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ インデックス？

$\footnotesize \textcolor{pink}{四国めたん:}$ はい、ヒープソートの原理の説明で、最初に 二分木 を作りましたわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ うむ

$\footnotesize \textcolor{pink}{四国めたん:}$ ここで、 親ノード のインデックスを$n$とすると 子ノード のインデックスが$2n + 1$と$2n + 2$となっていますわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ たしかに...

$\footnotesize \textcolor{pink}{四国めたん:}$ そして、インデックス$n$の ヒープ を生成するために、 子ノード の ヒープ を作成していましたわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ そうだったのだ

$\footnotesize \textcolor{pink}{四国めたん:}$ そして、インデックス$n$とインデックス$2n + 1$、$2n + 2$の値を比較して、最大値もしくは最小値をインデックス$n$の値に置き換えていましたわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ これでインデックス$n$の ヒープ が生成されていたのだ

$\footnotesize \textcolor{pink}{四国めたん:}$ まぁ、お分かりの通り、再帰関数を使うことができますわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ なるほどなのだ

#include <stdio.h>

void swap(int data[], int idx1, int idx2) {
  int temp = data[idx1];
  data[idx1] = data[idx2];
  data[idx2] = temp;
  return;
}

void heap(int data[], int root_idx, int last_idx) {
  int child_idx1 = root_idx * 2 + 1;
  int child_idx2 = root_idx * 2 + 2;
  if (child_idx2 > last_idx) {
    if (child_idx1 <= last_idx) {
      heap(data, child_idx1, last_idx);
      if (data[root_idx] < data[child_idx1]) {
        swap(data, root_idx, child_idx1);
      }
    }
  } else {
    heap(data, child_idx1, last_idx);
    heap(data, child_idx2, last_idx);
    if (data[root_idx] < data[child_idx1]) {
      if (data[child_idx1] < data[child_idx2]) {
        swap(data, root_idx, child_idx2);
      } else {
        swap(data, root_idx, child_idx1);
      }
    } else if (data[root_idx] < data[child_idx2]) {
      swap(data, root_idx, child_idx2);
    }
  }
  return;
}

$\footnotesize \textcolor{pink}{四国めたん:}$ まず、swap関数は配列"data"で、指定のインデックスのデータを入れ替えますわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ うむ

$\footnotesize \textcolor{pink}{四国めたん:}$ 次にheap関数は配列"data"で、指定のインデックス"root_idx"をルートとした 二分木 から ヒープ を生成しますわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ りょうかいなのだ

$\footnotesize \textcolor{pink}{四国めたん:}$ なお、 二分木 に使用するデータは、"data"配列中の"root_idx"から"last_idx"までですわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ うむ

$\footnotesize \textcolor{pink}{四国めたん:}$ "last_idx"以降のデータは既にソートされているか、配列の外なので、アクセス禁止ですわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ アクセスすると大変な目に合うのだ

$\footnotesize \textcolor{pink}{四国めたん:}$ 関数内では、まず、ルートのインデックスから子のインデックスを$2n + 1$と$2n + 2$で計算しますわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ ふむふむ

$\footnotesize \textcolor{pink}{四国めたん:}$ そして2番目の子のインデックスがデータ範囲外の場合は1番目の子のインデックスがデータ範囲に入っているか、確認しますわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ データ範囲外であれば何もしないのだ

$\footnotesize \textcolor{pink}{四国めたん:}$ データ範囲内であれば、1番目の子のインデックスをルートのインデックスとしてheap関数を再帰呼び出ししますわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ なるほどなのだ

$\footnotesize \textcolor{pink}{四国めたん:}$ 結果としてルートインデックスの値が子のインデックスの値より小さい場合には、データを交換しますわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ うむ

$\footnotesize \textcolor{pink}{四国めたん:}$ 次に、2番目の子のインデックスがデータ範囲内の場合には、1番目の子のインデックスもデータの範囲内となりますわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ とうぜんなのだ

$\footnotesize \textcolor{pink}{四国めたん:}$ なので、1番目と2番目の子のインデックスをルートのインデックスとしてheap関数を再帰呼び出ししますわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ なるほどなのだ

$\footnotesize \textcolor{pink}{四国めたん:}$ 結果としてルートインデックスの値が子のインデックスの値より小さい場合には、データを交換しますわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ うむ

$\footnotesize \textcolor{pink}{四国めたん:}$ これらの操作で 二分木 全体が ヒープ として整えられますわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ なるほどなのだ

ヒープソート関数

$\footnotesize \textcolor{pink}{四国めたん:}$ 次にheap関数を使ってソートをおこなうheap_sort関数を実装しますわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ よろしくなのだ

void heap_sort(int data[], int size) {
  for (int last_idx = size - 1; last_idx > 0; last_idx--) {
    heap(data, 0, last_idx);
    swap(data, 0, last_idx);
  }
  return;
}

$\footnotesize \textcolor{pink}{四国めたん:}$ まず、引数にはソートするデータが収められた配列"data"とそのサイズ"size"をセットしますわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ ふむ

$\footnotesize \textcolor{pink}{四国めたん:}$ 配列"data"中、heap関数で ヒープ を生成する範囲は、インデックス0からソートが完了していない範囲としますわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ うむ

$\footnotesize \textcolor{pink}{四国めたん:}$ ですので、最後のインデックス"last_idx"は、配列の最後の要素から順番に1つづつ減っていくようにしますわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ for文を使っているのだ

$\footnotesize \textcolor{pink}{四国めたん:}$ ヒープ 生成後はルートと最後のデータを入れ替えますわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ うむ

$\footnotesize \textcolor{pink}{四国めたん:}$ 最終的に配列内のデータはソートされますわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ りょうかいなのだ

メイン関数

$\footnotesize \textcolor{pink}{四国めたん:}$ それでは、実際のデータを使ってソートしてみましょう

int main(int argc, char* argv[]) {
  int data[] = {4, 6, 5, 2, 1, 3};
  int size = sizeof(data) / sizeof(int);
  heap_sort(data, size);
  for (int i = 0; i < size; i++) {
    printf("%d ", data[i]);
  }
  printf("\n");
  return 0;
}

$\footnotesize \textcolor{pink}{四国めたん:}$ まず、適当に数値を入れた配列"data"を用意しますわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ うむ

$\footnotesize \textcolor{pink}{四国めたん:}$ 引数に値を指定してheap_sortを呼び出しますわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ 最後に"data"内の整数を出力して、ソートされていることを確認しているのだ

$\footnotesize \textcolor{pink}{四国めたん:}$ それでは実行してみましょう

$\footnotesize \textcolor{lime}{ずんだもん:}$ ちゃんとソートされていることを確認できるのだ

まとめ

$\footnotesize \textcolor{pink}{四国めたん:}$ お疲れさまでした

$\footnotesize \textcolor{lime}{ずんだもん:}$ おつかれさまなのだ

$\footnotesize \textcolor{pink}{四国めたん:}$ 以上で ヒープソート を終了しますわ

$\footnotesize \textcolor{lime}{ずんだもん:}$ ところで ヒープソート は結構速いのか？

$\footnotesize \textcolor{pink}{四国めたん:}$ マージソート と同様に、意外と速い部類のソートですわね

$\footnotesize \textcolor{lime}{ずんだもん:}$ なるほどなのだ