JavaScriptで変化点検出がしたい
時系列データを触っているとなにか異常があった、モードが変わったことを検知したくなります。
そうすると機械学習に頼ることになるわけですが、できればパラメータチューニングを最小限にしたい。
調べてみると特異スペクトル変換(Singular Spectrum Transformation)という方法がよさそうです。
- ノンパラメトリック(分布を仮定しなくてよい)
- ノイズに強い
- 決めるべき変数が少ない
いいことづくし。
唯一欠点として計算量が多いというのがありますが、ビッグデータを扱うわけでもない個人の解析の範疇であればマシンスペックが潤沢な現代においてあまり気にする必要もないでしょう。
というわけで特異スペクトル変換をJavaScript(TypeScript)で行ってみます[1]。
特異スペクトル変換
詳しい理論やアルゴリズムの説明は書籍[2][3]、論文[4][5][6]に譲りますが大雑把なイメージです。

ある時刻の前後で時系列データを少しずつずらしていくつも取り出した行列同士を比較してその差異を評価します。
このとき特異値分解(SVD)を使うため、行列のサイズによっては計算が重たくなります[7]。
SVDもJavaScriptでやるのはめんどうなのですが、こちらの記事の処理をまるまる流用します。
const sst = (x: number[], window: number, options?: SstOptions): (number | undefined)[] => {
const T = x.length;
const lag = options?.lag ? options.lag : Math.ceil(window / 2);
const k1 = options?.trajectory?.k ? options.trajectory.k : Math.ceil(window / 2);
const p1 = options?.trajectory?.m ? options.trajectory.m : Math.min(k1, 2);
const k2 = options?.test?.k ? options.test.k : Math.ceil(window / 2);
const p2 = options?.test?.m ? options.test.m : Math.min(k2, 2);
if (lag < 1) {
throw new Error("lag is must be more than 0.");
}
if (k1 < 1) {
throw new Error("col of trajectory matrix is must be more than 0.");
}
if (k1 < p1) {
throw new Error("m of trajectory is must be less than col of trajectory.");
}
if (k2 < 1) {
throw new Error("col of test matrix is must be more than 0.");
}
if (k2 < p2) {
throw new Error("m of test is must be less than col of test.");
}
const start = window + k1 - 1;
const end = T - lag;
if (start > T - 1 || end < 0 || T + lag - k2 - window < 0) {
throw new Error("out of range.");
}
const ret: (number | undefined)[] = Array(T);
for (let i = start; i <= end; i++) {
const trajectory = embed(x, i, window, k1);
const [q1, U1] = svd(trajectory);
const order1 = indexOrder(q1);
const test = embed(x, i + lag, window, k2);
const [q2, U2] = svd(test);
const order2 = indexOrder(q2);
const X1 = recomposition(U1, order1.slice(0, p1).map((v) => {
return v.index
}));
const X2 = recomposition(U2, order2.slice(0, p2).map((v) => {
return v.index
}));
const [q] = svd(mult(transpose(X1), X2), options?.svd);
const order = indexOrder(q);
ret[i] = 1 - order[0].value ** 2;
}
return ret;
}
export interface SstOptions {
lag?: number;
trajectory?: {
k?: number;
m?: number;
};
test?: {
k?: number;
m?: number;
};
svd?: SvdOptions
}
const recomposition = (mat: number[][], cols: number[]): number[][] => {
const ret: number[][] = [];
for (let i = 0; i < mat.length; i++) {
const row: number[] = [];
cols.forEach((j) => {
row.push(mat[i][j])
});
ret.push(row);
}
return ret;
}
const transpose = (mat: number[][]): number[][] => {
const ret: number[][] = [];
const m = mat.length;
const n = mat[0]?.length;
for (let i = 0; i < n; i++) {
const row = [];
for (let j = 0; j < m; j++) {
row.push(mat[j][i]);
}
ret.push(row);
}
return ret;
}
const mult = (mat1: number[][], mat2: number[][]): number[][] => {
if (mat1[0]?.length !== mat2.length) {
throw new Error("Matrices don't match size.");
}
const ret: number[][] = [];
for (let i = 0; i < mat1.length; i++) {
const row = [];
for (let j = 0; j < mat2[0].length; j++) {
let elm = 0;
for (let k = 0; k < mat1[0].length; k++) {
elm += mat1[i][k] * mat2[k][j];
}
row.push(elm)
}
ret.push(row);
}
return ret;
}
const indexOrder = (arr: number[]): {
value: number;
index: number;
}[] => {
const ret = arr.map((value, index) => {
return {
value,
index
}
});
ret.sort((a, b) => {
if (a.value < b.value) return 1;
if (a.value > b.value) return -1;
return 0;
});
return ret
}
const embed = (arr: number[], t: number, w: number, k: number): number[][] => {
if (t - k - w + 1 < 0 || t > arr.length) {
throw new Error("out of range.");
}
const X = mZeros(w, k);
for (let i = 0; i < w; i++) {
for (let j = 0; j < k; j++) {
X[i][j] = arr[t - (k - j) - w + 1 + i]
}
}
return X
}
const mZeros = (row: number, col?: number): number[][] => {
if (row < 1) {
throw new Error("row must be more than 0.");
}
if (col && col < 1) {
throw new Error("col must be more than 0.");
}
const m = row;
const n = col ? col : row;
const ret: number[][] = [];
for (let i = 0; i < m; i++) {
ret.push((Array(n) as number[]).fill(0));
}
return ret;
}
sstに必要なパラメータは時系列データの他にwindow, lag, trajectory.k, trajectory.m, test.k, test.mのみです。
論文4によると、若干の計算方法の違いはあるため全く同じとはいかないかもしれませんが、
- ウインドウサイズ
windowは変化点の発生間隔よりも大きくする。 - 履歴行列の列の数
trajectory.kはしばしばwindowと同じ値が使われる。 - テスト行列の列の数
test.kは履歴行列の列の数ほど敏感ではないため、1からwindowの範囲で適当に決めてよい。 - ラグ
lagはテスト行列の及ぶ範囲の中心がちょうどtのあたりにくるよう、−(window + test.k)/2とするのがよい。
とされています。
また、左特異ベクトルの本数trajectory.mとtest.mは、あまり大きく設定してもノイズの影響が出てしまうので小さめな値(2~5)を設定しておけばよいです[8]。
厳密にやりたければ特異値の寄与率から決定するように改良してもいいでしょう。
ということで、パラメータで悩む必要があるのはwindowくらいで、他はほぼ自動的に決まるか、適当でも大して影響がないパラメータとなります。素敵。
文献[2]のP203で試している例を実際に計算してみましょう。
こちらで公開されているECG dataset used in slide 30から3001-6000のデータを抜き出し、本のサンプルの通りwindow=50, lag=12, trajectory.k=25, trajectory.m=2, test.k=25, test.m=2で実行します。


本を持っている人は見比べてみてください。人目で判断する限り同じ結果になっていると思います。
ピークを自動で見つける
さて、異常度スコアは計算できたので、グラフのピークが立っているところが変化点であることはわかりますが、これを自動で判別する方法はないでしょうか。
文献には特には載っていませんでした。どれもグラフを出すところで終わりです。
データの性質によって最大値が全然違うため単純に閾値というのもちょっと難しいです。
それらしいアルゴリズムを自分で考えてみることにします。
const find = (values: (number | undefined)[], options?: PeekFind): boolean[] => {
const neighbor = options?.neighbor ? (options.neighbor > values.length ? values.length : options.neighbor) : 1;
const threshold = typeof options?.threshold === "undefined" ? -Infinity : options.threshold;
if (neighbor < 1) {
throw new Error("neighbor is must be more than 0.");
}
const ret: boolean[] = [];
for (let i = 0; i < values.length; i++) {
if (typeof values[i] !== "undefined" && values[i] as number >= threshold) {
let peek = true;
let leftDrop = false, rightDrop = false;
const center = values[i] as number;
for (let j = 1; j <= neighbor; j++) {
if (typeof values[i + j] !== "undefined") {
const right = values[i + j] as number;
if (!rightDrop) {
if (right > center) {
peek = false;
break;
}
if (right < center) {
rightDrop = true;
}
} else {
if (right >= center) {
peek = false;
break;
}
}
}
if (typeof values[i - j] !== "undefined") {
const left = values[i - j] as number;
if (!leftDrop) {
if (left > center) {
peek = false;
break;
}
if (left < center) {
leftDrop = true;
}
} else {
if (left >= center) {
peek = false;
break;
}
}
}
}
ret.push(rightDrop && leftDrop && peek);
} else {
ret.push(false);
}
}
return ret;
}
interface PeekFind {
neighbor?: number;
threshold?: number;
}

引数で渡したneighbor(デフォルトでは1)分だけ隣の点と比較し、左右両方向とも減少していればピークだと判定します。
この例だとneighbor=1で、ピークはt=3, 6です。

この例だとneighbor=3とした場合、t=6がピークでなくなります(t=3よりも小さいため)。
またt=2,3は同じ値ですが、neighbor=3内で値が減少するので共にピークと判定されます。
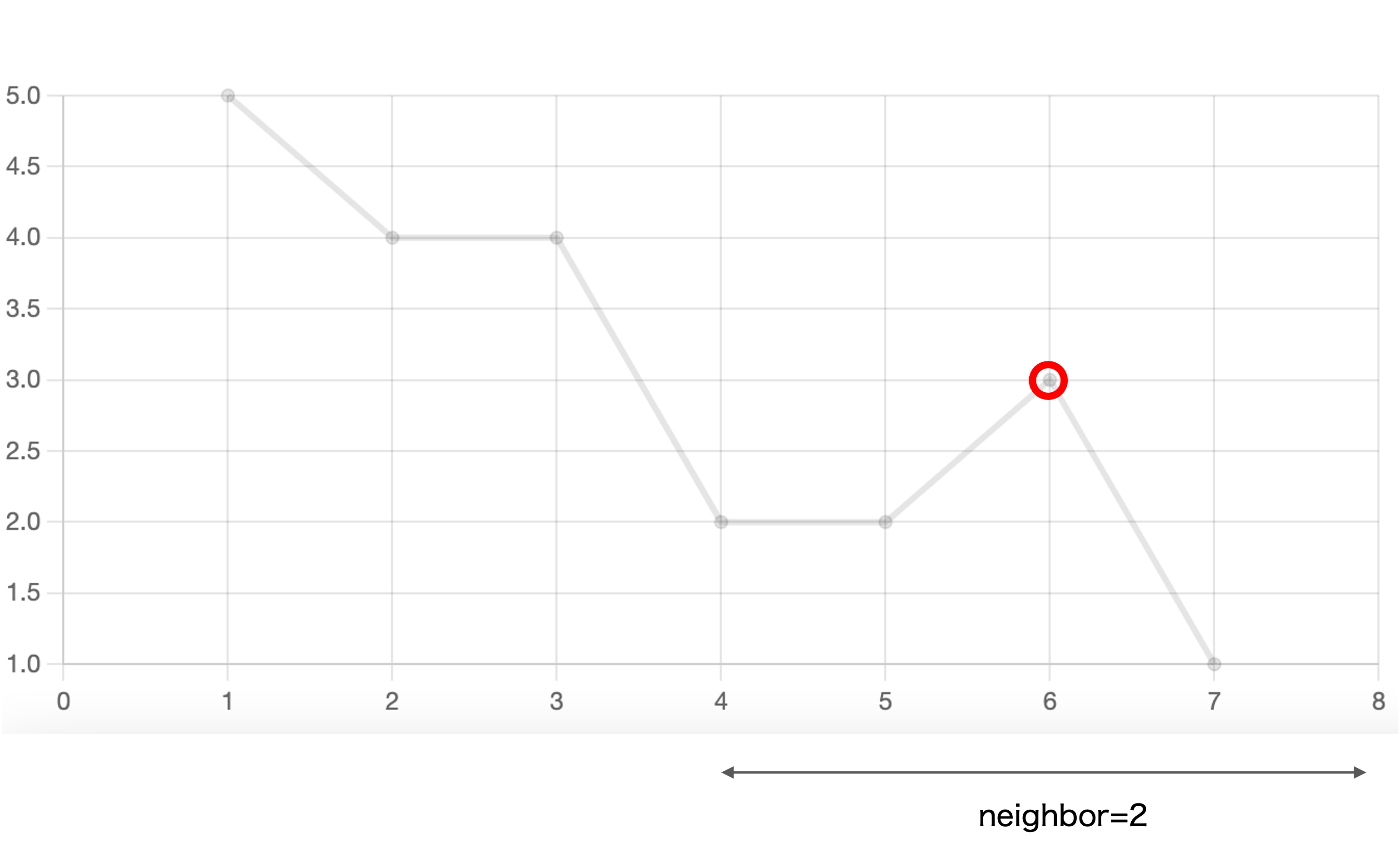
この例ではt=1は左側が減少することなく見切れてしまうため、ピークでないと判定されます。
引数で渡したthresholdが渡された場合は、値がそれ以上かも条件に加わります。

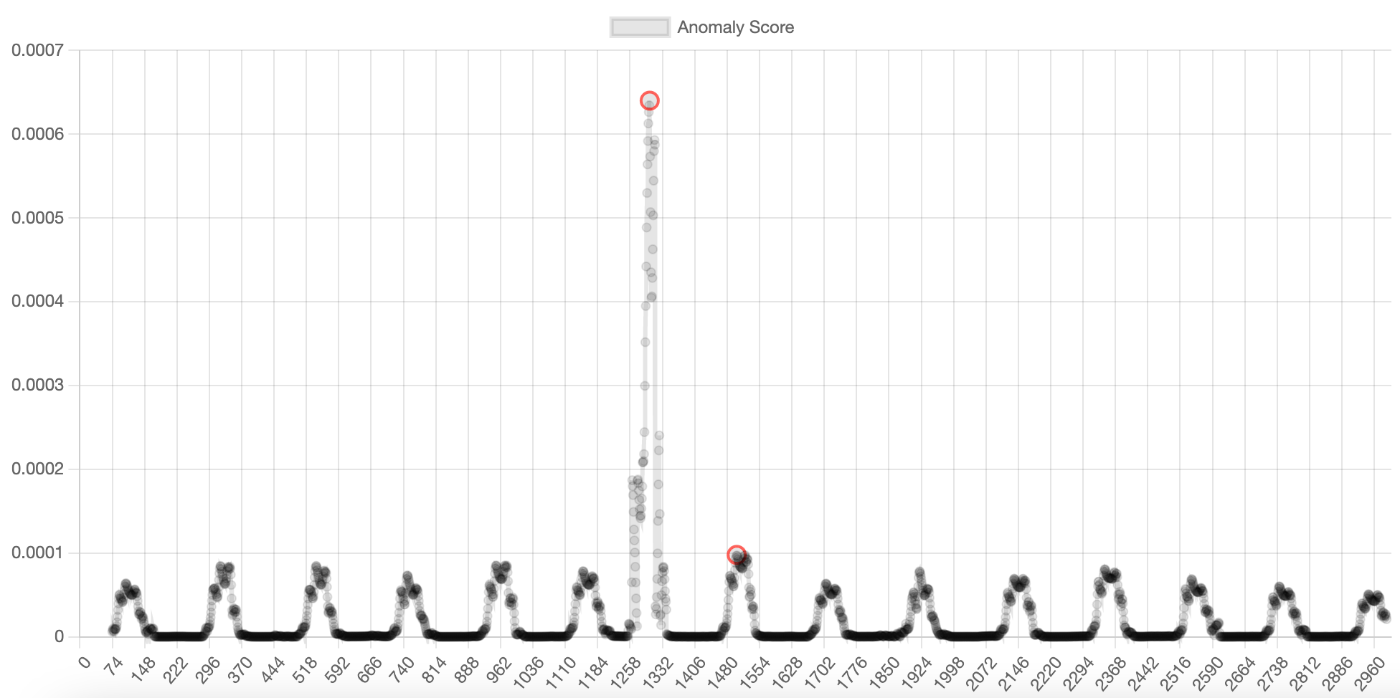
デフォルト(neighbor=1)で判定した例です。
きちんとピーク(赤丸)の判定ができてますが、多すぎますね。

neighborをwindowと同じ値(50)にしてみました。
変化の発生間隔よりも大きくするといい感じですが、これも調節すべきパラメータとなってしまいます。
ただしthresholdを設定していないため、値が小さい時刻でもピーク判定されてしまっています。
四分位範囲で過検出を減らす
ピークは外れ値となるケースがほとんどでしょう。
第3四分位数 + 1.5 × (第3四分位数 - 第1四分位数)を超える値を大きい方の外れ値とする検出法がよく使われているので、その値をthresholdとしてピークを探すことにしましょう。
const quartile = (values: (number | undefined)[]): {
min: number;
max: number;
first: number;
second: number;
third: number;
iqr: number;
} => {
const orders = (values.filter((v) => typeof v !== "undefined") as number[]).sort((a, b) => {
if (a < b) return 1;
if (a > b) return -1;
return 0;
});
if (orders.length < 1) {
throw new Error("values must contain at least one number.");
}
const max = orders[0];
const min = orders[orders.length - 1];
const largeStart = 0, smallEnd = orders.length - 1;
let second, third, first, largeEnd, smallStart;
if (orders.length % 2 !== 0) {
const center = Math.floor(orders.length / 2);
second = orders[center];
largeEnd = center - 1;
smallStart = center + 1;
} else {
largeEnd = orders.length / 2 - 1;
smallStart = orders.length / 2;
second = (orders[largeEnd] + orders[smallStart]) / 2;
}
const largeLength = largeEnd - largeStart + 1;
if (largeLength % 2 !== 0) {
third = orders[Math.floor(largeLength / 2)];
} else {
third = (orders[largeLength / 2 - 1] + orders[largeLength / 2]) / 2;
}
const smallLength = smallEnd - smallStart + 1;
if (smallLength % 2 !== 0) {
first = orders[smallStart + Math.floor(smallLength / 2)];
} else {
first = (orders[smallStart + smallLength / 2 - 1] + orders[smallStart + smallLength / 2]) / 2;
}
return {
min,
max,
first,
second,
third,
iqr: third - first
}
}
const q = quartile(scores);
const peeks = find(scores, {
neighbor: 50, // ほかは10など
threshold: q.third + q.iqr * 1.5
})
neighbor=50でと赤丸が減りました。
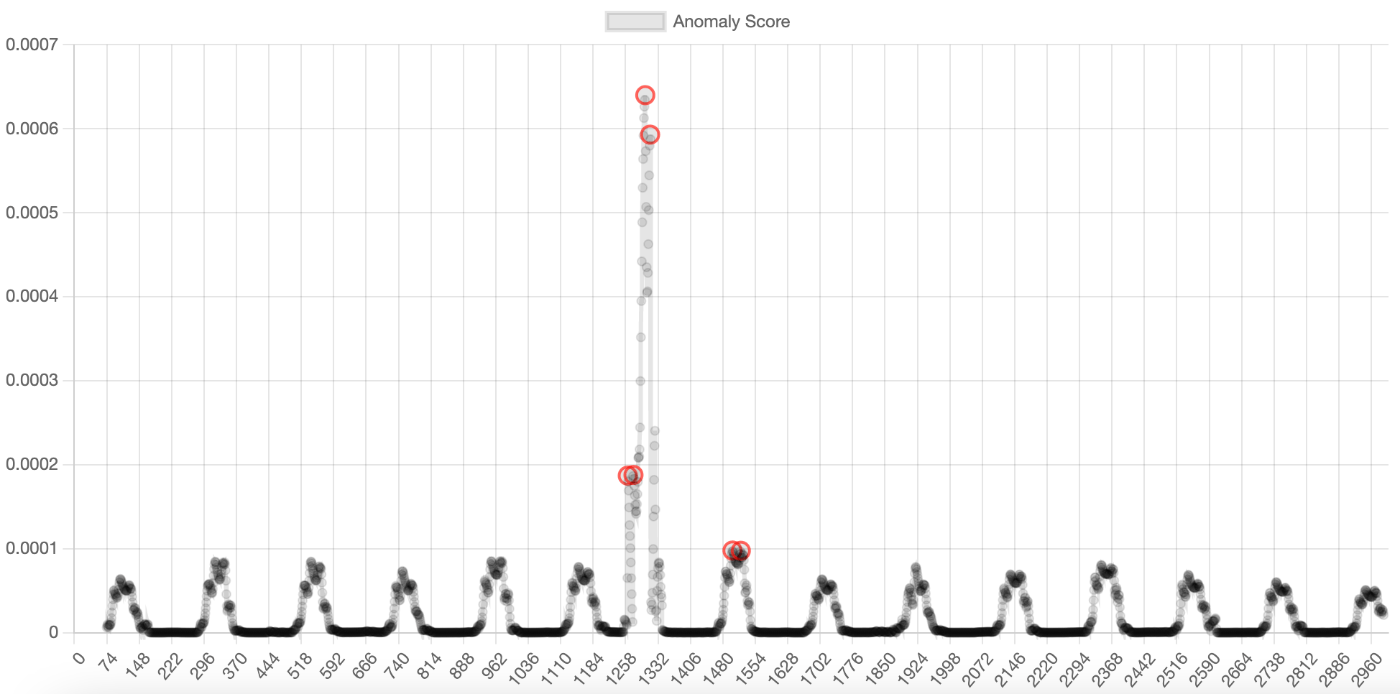
neighbor=10でも、小さいピーク候補が排除することができています。
これで雑にneighborを設定しても過検出を防ぐことができそうです。
今回は対象とするデータ全域を四分位数の計算対象としましたが、これにもwindowを設けてもよさそうです。
このほかにも最大値のX割がけした値をthresholdにする手も考えられます。
まとめ
文献を元にJavaScriptで特異スペクトル変換を利用した変化点検出を行いました。
より精度を出したければ別のアルゴリズムやディープラーニングをゴリゴリとやっていくべきですが、特異スペクトル変換は設定すべきパラメータが少なく、テキトウにやってもそれらしい結果が出せる点が魅力です。
算出されるスコアから自動でピークを判定する方法も考案しました。
後日、論文[4-6]で紹介されているSVDを利用しないLanczos法による解法を実装したい。
Discussion