PyTorchによるTadGAN(時系列異常検知)
- 時系列データの異常検知をしたい
- 教師なし(ラベルなし)がいい
- PyTorch('1.11.0+cu113')を使いたい
TadGAN: Time Series Anomaly Detection Using Generative Adversarial Networks(2020年9月の論文)が良さそうである。
Tensorflowでよければ orion-ml というライブラリがある。
論文の執筆者もコントリビュートしているので本家と言っていい。
PyTorchでの実装もいくつがあるか、理解のために自前実装していく。
ということで本記事はTadGANをPyTorchで実装してみた際のコードと、素人がGANを一から調べた過程のメモである。
実装
先にコードを提示する。
import os
import torch
import torch.optim as optim
from torch.utils.data import Dataset, DataLoader
import numpy as np
from abc import ABCMeta, abstractmethod
from scipy import stats
def set_seed(seed=1):
torch.manual_seed(seed)
torch.cuda.manual_seed(seed)
torch.backends.cudnn.deterministic = True
torch.use_deterministic_algorithms = True
class Encoder(torch.nn.Module):
def __init__(self, window_size, latent_dim, hidden_size=100):
super().__init__()
self.lstm = torch.nn.LSTM(input_size=window_size, hidden_size=hidden_size,
num_layers=1, bidirectional=True, batch_first=True)
self.dense = torch.nn.Linear(
in_features=hidden_size*2, out_features=latent_dim)
def forward(self, x):
x, (hn, cn) = self.lstm(x)
z = self.dense(x)
return (z)
class Decoder(torch.nn.Module):
def __init__(self, window_size, latent_dim, hidden_size=64):
super().__init__()
self.lstm = torch.nn.LSTM(
input_size=latent_dim, hidden_size=hidden_size, num_layers=2, bidirectional=True, batch_first=True)
self.dense = torch.nn.Linear(
in_features=hidden_size*2, out_features=window_size)
def forward(self, z):
z, (hn, cn) = self.lstm(z)
x = self.dense(z)
return (x)
class Cx(torch.nn.Module):
def __init__(self, window_size, state_dim=1, cnn_blocks=4):
super().__init__()
layers = [['Conv1d_0', torch.nn.Sequential(
torch.nn.Conv1d(in_channels=state_dim,
out_channels=64, kernel_size=5, padding=2),
torch.nn.LeakyReLU(negative_slope=0.2),
torch.nn.Dropout(0.25)
)]]
if cnn_blocks > 1:
for i in range(1, cnn_blocks):
layers.append(['Conv1d_{}'.format(i), torch.nn.Sequential(
torch.nn.Conv1d(in_channels=64,
out_channels=64, kernel_size=5, padding=2),
torch.nn.LeakyReLU(negative_slope=0.2),
torch.nn.Dropout(0.25)
)])
layers.append(['Flatten', torch.nn.Flatten()])
layers.append(['Dense', torch.nn.Linear(
in_features=64*window_size, out_features=1)])
self.layers = torch.nn.ModuleDict(layers)
def forward(self, x):
for layer in self.layers.values():
x = layer(x)
return x
class Cz(torch.nn.Module):
def __init__(self, latent_dim):
super().__init__()
layers = [['dense_0', torch.nn.Sequential(
torch.nn.Linear(in_features=latent_dim, out_features=100),
torch.nn.LeakyReLU(negative_slope=0.2),
torch.nn.Dropout(0.2)
)], ['dense_1', torch.nn.Sequential(
torch.nn.Linear(in_features=100, out_features=100),
torch.nn.LeakyReLU(negative_slope=0.2),
torch.nn.Dropout(0.2)
)], ['dense_2', torch.nn.Sequential(
torch.nn.Linear(in_features=100, out_features=1)
)]]
self.layers = torch.nn.ModuleDict(layers)
def forward(self, z):
for layer in self.layers.values():
z = layer(z)
return z
class ProcessedDataset(Dataset, metaclass=ABCMeta):
"""
Implement __getitem__ to return (start_index, np.array(state_size, window_size))
"""
@property
@abstractmethod
def window_size(self):
raise NotImplementedError()
@property
@abstractmethod
def state_size(self):
raise NotImplementedError()
def _euclideandistance(a, b):
return np.sqrt(np.sum((a - b)**2))
def _minVal(values):
return sorted(values, key=lambda x: x['cost'])[0]
def _dtw(ts1, ts2):
ret = [[None for _ in range(len(ts2))] for _ in range(len(ts1))]
np.zeros((len(ts1), len(ts2)))
ret[0][0] = {'cost': _euclideandistance(ts1[0], ts2[0]), 'path': [-1, -1]}
for i in range(1, len(ts1)):
ret[i][0] = {'cost': ret[i - 1][0]['cost'] +
_euclideandistance(ts1[i], ts2[0]), 'path': [i - 1, 0]}
for j in range(1, len(ts2)):
ret[0][j] = {'cost': ret[0][j - 1]['cost'] +
_euclideandistance(ts1[0], ts2[j]), 'path': [0, j - 1]}
for i in range(1, len(ts1)):
for j in range(1, len(ts2)):
mv = _minVal([
{
'cost': ret[i - 1][j]['cost'],
'path': [i - 1, j]
},
{
'cost': ret[i][j - 1]['cost'],
'path': [i, j - 1]
},
{
'cost': ret[i - 1][j - 1]['cost'],
'path': [i - 1, j - 1]
}]
)
ret[i][j] = {
'cost': mv['cost'] + _euclideandistance(ts1[i], ts2[j]),
'path': mv['path']
}
return ret[-1][-1]
class TadGanError(Exception):
def __init__(self, message):
super().__init__(message)
class TadGAN:
def __init__(self, dataset: ProcessedDataset,
batch_size=64,
lr=0.0005,
num_critics=5,
latent_dim=20,
loss_rate_critics=[1, 1, 10],
loss_rate_generator=[1, 10],
encoder_hidden_size=100,
decoder_hidden_size=64,
cx_cnn_blocks=4):
self.dataset = dataset
self.window_size = dataset.window_size
self.state_size = dataset.state_size
self.step_size = int(dataset[1][0] - dataset[0]
[0])
if self.step_size < 1:
raise TadGanError('invalid: step size of dataset')
self.batch_size = batch_size
self.lr = lr
self.num_epoch = 0
self.num_critics = num_critics
self.latent_dim = latent_dim
self.loss_rate_critics = loss_rate_critics
self.loss_rate_generator = loss_rate_generator
window_size = dataset.window_size
self.device = torch.device(
'cuda:0' if torch.cuda.is_available() else 'cpu')
self.encoder = Encoder(window_size, latent_dim, hidden_size=encoder_hidden_size).to(self.device)
self.decoder = Decoder(window_size, latent_dim, hidden_size=decoder_hidden_size).to(self.device)
self.cx = Cx(window_size, state_dim=self.state_size, cnn_blocks=cx_cnn_blocks).to(self.device)
self.cz = Cz(latent_dim).to(self.device)
self.optimizer_encoder = torch.optim.Adam(
self.encoder.parameters(), lr=lr)
self.optimizer_decoder = torch.optim.Adam(
self.decoder.parameters(), lr=lr)
self.optimizer_cx = torch.optim.Adam(self.cx.parameters(), lr=lr)
self.optimizer_cz = torch.optim.Adam(self.cz.parameters(), lr=lr)
@staticmethod
def gradient_penalty(model, real, fake, device):
alpha = torch.randn((real.size(0), 1, 1), device=device)
interpolates = (alpha * real + ((1 - alpha) * fake)
).requires_grad_(True)
model_interpolates = model(interpolates)
grad_outputs = torch.ones(
model_interpolates.size(), device=device, requires_grad=False)
gradients = torch.autograd.grad(
outputs=model_interpolates,
inputs=interpolates,
grad_outputs=grad_outputs,
create_graph=True,
retain_graph=True,
only_inputs=True,
)[0]
norm = gradients.norm(2, dim=2)
gradient_penalty = torch.mean((norm - 1) ** 2)
return gradient_penalty
def __critic_x_iteration(self, x, z):
self.cx.train(True)
self.decoder.train(True)
self.optimizer_cx.zero_grad()
fake_x = self.decoder(z)
real_output = torch.squeeze(self.cx(x))
fake_output = torch.squeeze(self.cx(fake_x))
real_loss = torch.mean(real_output)
fake_loss = torch.mean(fake_output)
gp_loss = self.gradient_penalty(self.cx, x, fake_x, self.device)
loss = self.loss_rate_critics[0]*fake_loss - \
self.loss_rate_critics[1]*real_loss + \
self.loss_rate_critics[2]*gp_loss
loss.backward()
self.optimizer_cx.step()
return loss.item()
def __critic_z_iteration(self, z, x):
self.cz.train(True)
self.encoder.train(True)
self.optimizer_cz.zero_grad()
fake_z = self.encoder(x)
real_output = torch.squeeze(self.cz(z))
fake_output = torch.squeeze(self.cz(fake_z))
real_loss = torch.mean(real_output)
fake_loss = torch.mean(fake_output)
gp_loss = self.gradient_penalty(self.cz, z, fake_z, self.device)
loss = self.loss_rate_critics[0]*fake_loss - \
self.loss_rate_critics[1]*real_loss + \
self.loss_rate_critics[2]*gp_loss
loss.backward()
self.optimizer_cz.step()
return loss.item()
def __encoder_decoder_iteration(self, x, z):
self.encoder.train(True)
self.decoder.train(True)
self.cx.train(False)
self.cz.train(False)
self.optimizer_encoder.zero_grad()
self.optimizer_decoder.zero_grad()
fake_x = self.decoder(z)
fake_z = self.encoder(x)
reconstructed_x = self.decoder(fake_z)
fake_x_output = torch.squeeze(self.cx(fake_x))
fake_z_output = torch.squeeze(self.cz(fake_z))
fake_x_loss = torch.mean(fake_x_output)
fake_z_loss = torch.mean(fake_z_output)
loss = - self.loss_rate_generator[0]*(fake_x_loss + fake_z_loss) + self.loss_rate_generator[1] * \
torch.sqrt(torch.sum(torch.square(x - reconstructed_x)))
loss.backward()
self.optimizer_encoder.step()
self.optimizer_decoder.step()
return loss.item()
@property
def raw(self):
length = self.window_size + self.step_size * (len(self.dataset) - 1)
ret = np.zeros((length, self.state_size))
for row in self.dataset:
start = row[0]
values = row[1]
for i in range(self.window_size):
index = int(i + start)
ret[index, :] = values[:, i]
self.__raw = ret
return ret
def train(self, num_epoch=100, debug=False):
cx_loss = []
cz_loss = []
g_loss = []
train_loader = DataLoader(self.dataset, batch_size=self.batch_size,
drop_last=True, shuffle=True, num_workers=os.cpu_count())
for epoch in range(1, num_epoch+1):
self.num_epoch += 1
epoch_cx_loss = []
epoch_cz_loss = []
epoch_g_loss = []
for batch, data in enumerate(train_loader):
x = data[1].float().to(self.device)
z = torch.empty(self.batch_size, 1, self.latent_dim).uniform_(
0, 1).to(self.device)
loss = self.__critic_x_iteration(x, z)
epoch_cx_loss.append(loss)
loss = self.__critic_z_iteration(z, x)
epoch_cz_loss.append(loss)
if (batch + 1) % self.num_critics == 0:
epoch_g_loss.append(self.__encoder_decoder_iteration(x, z))
cx_loss.append(np.mean(np.array(epoch_cx_loss)))
cz_loss.append(np.mean(np.array(epoch_cz_loss)))
g_loss.append(np.mean(np.array(epoch_g_loss)))
if debug:
print('Epoch: {}/{}, [Cx loss: {}] [Cz loss: {}] [G loss: {}]'.format(
epoch, num_epoch, cx_loss[-1], cz_loss[-1], g_loss[-1]))
return (np.array(cx_loss), np.array(cz_loss), np.array(g_loss))
def reconstruct(self, values):
if values.shape[1] != self.state_size:
raise TadGanError('invalid: values unmatch state_size')
self.decoder.train(False)
self.encoder.train(False)
reconstructed = []
start = 0
end = self.window_size
while end <= len(values):
fake = self.encoder(torch.tensor(values[start:end], device=self.device).view(
1, self.state_size, self.window_size).float())
reconstructed.append(self.decoder(fake).detach()[
0].transpose(1, 0).tolist())
start+=self.step_size
end+=self.step_size
num_row = len(reconstructed)
length = self.window_size + self.step_size * (num_row - 1)
ret = []
for i in range(length):
diagonal = []
for j in range(max(0, i - length + self.window_size), min(i + 1, self.window_size)):
if i - j < num_row:
diagonal.append(reconstructed[i - j][j])
if len(diagonal) > 0:
ret.append(np.median(np.array(diagonal), axis=0).tolist())
return np.array(ret)
def anomaly_score(self, raw, reconstructed, distance='point', combination='add', alpha=None, score_window=10):
if raw.shape != reconstructed.shape:
raise TadGanError('invalid: raw and reconstructed are not same size.')
self.cx.train(False)
if distance == 'dtw':
if len(raw) < score_window:
score_window = len(raw)
if score_window < 0:
score_window = 1
dtw_length = (score_window // 2) * 2 + 1
dtw_half_length = dtw_length // 2
distance = []
for i in range(len(raw) - dtw_length):
distance.append(
_dtw(raw[i:i + dtw_length], reconstructed[i:i + dtw_length])['cost'])
reconstructed_score = np.clip(stats.zscore(np.array(distance)), a_min=0, a_max=None)
reconstructed_score = np.pad(reconstructed_score, (dtw_half_length, len(raw) - len(distance) - dtw_half_length),
'constant', constant_values=(0, 0))
else:
reconstructed_score = np.sqrt(
np.sum((raw - reconstructed)**2, axis=1))
reconstructed_score = np.clip(stats.zscore(reconstructed_score), a_min=0, a_max=None)
if combination is None:
return reconstructed_score
if alpha is None:
alpha = 0.5 if combination == 'add' else 1
if alpha > 1:
alpha = 1
if alpha < 0:
alpha = 0
cxr_rect = []
start = 0
end = self.window_size
while end <= len(reconstructed):
cxr_rect.append(np.repeat(self.cx(torch.tensor(reconstructed[start:end].transpose(1, 0)).view(
1, self.state_size, self.window_size).to(self.device).float()).detach().tolist()[0][0], self.window_size).tolist())
start+=self.step_size
end+=self.step_size
length = self.window_size + self.step_size * (len(cxr_rect) - 1)
critic_score = []
for i in range(length):
cxr_inter = []
for j in range(max(0, i - length + self.window_size), min(i + 1, self.window_size)):
cxr_inter.append(cxr_rect[i - j][j])
if len(cxr_inter) > 1:
cxr_inter = np.array(cxr_inter)
try:
critic_score.append(cxr_inter[np.argmax(
stats.gaussian_kde(cxr_inter)(cxr_inter))])
except np.linalg.LinAlgError:
critic_score.append(np.median(cxr_inter))
else:
critic_score.append(cxr_inter[0])
critic_score = np.clip(-stats.zscore(critic_score), a_min=0, a_max=None)
if combination == 'mult':
return alpha * reconstructed_score * critic_score
return alpha * reconstructed_score + (1 - alpha) * critic_score
GANって何
のあたりを読めばだいたい理解できるので割愛。
Generator(偽物を作り出す)とDiscriminator(本物と偽物を区別する)を作り、ディープラーニングで精度をあげていく。
最終的に出来上がったGeneratorを利用すると、精度の高いダミーデータが作れる。
GANといえば画像生成のイメージがあるが、別に画像以外にだって使える。
これを、
- 本物の時系列データ(異常値を含むかもしれない)からGeneratorの入力値となる形式に変換する
- 変換された値からGeneratorで元の形式の時系列データを生成
- 元のデータと生成されたデータでズレがあればそれは異常値だ
と応用するのがTadGAN。
GANの周辺知識
というところまで理解してから論文やライブラリの実装コードを読み進めるが、やっぱりわからない概念が多い。
- criticってなんじゃい、Discriminatorはどこ行った
- gradient penaltyって何
- ハイパーパラメータはなんでその値にしてるの
GANの周辺知識を得ないと太刀打ちできなさそうなので、以下でざっと学ぶ。
- CycleGANをpytorchで実装してみた
- GANからWasserstein GANへ
- [DL輪読会]Wasserstein GAN/Towards Principled Methods for Training Generative Adversarial Networks
- 今さら聞けないGAN(4) WGAN
- GANの学習安定化テクニック
- Wasserstein GAN
- Improved Training of Wasserstein GANs
初学者だから調べるのに苦労したが
- criticはWassersteinGANの文脈ででてくる。
- DCGANくらいシンプルなら場合はいいが、ある程度以上複雑になる場合は、WGAN-gpのテクニックが必須になってくる。
- ハイパーパラメータは学習安定化テクニックやCycleGAN、WassersteinGANの論文中に出てくる値がわりとそのまま採用されている。
ことがわかりスッキリする。
実装時のメモ
GeneratorとDiscriminator
Generator(EncoderとDecoder)、Discriminator(CxとCz)のモデルを作る。
モデルは扱うデータごとに工夫の余地があるところだが、ここではなるべく元論文に忠実にいく。
Generator(EncoderとDecoder)
元論文に書かれているままに実装。
隠れ層の数や潜在変数の次元のデフォルト値も元論文からそのまま拝借する。
Discriminator(CxとCz)
元論文だけでは実装イメージがまったくわかなかったので、Orionを大いに参考にさせてもらう。
Dropoutの率やkernelのサイズなんて初学者にはわからない。
機械学習系の論文は作者によるコードが公開されていることが多いため、秘伝のタレとされがちな部分も見えるのがとても助かる。
Conv1dを繰り返すことでチャンネル数が減っていく処理がめんどくさかったのでpaddingをいれてチャンネル数を維持する実装にしている。
データの読み込み
Datasetを拡張したProcessedDatasetというクラスを作ったので、これをさらに解析したいデータに合わせて拡張してもらう。
window_sizeとstate_sizeをメンバとして持つこと、各行は(start_index, np.array(state_size, window_size))の形で返すことがお約束。
実行クラス
self.device = torch.device(
'cuda:0' if torch.cuda.is_available() else 'cpu')
によりGPUが使える環境なら勝手にGPUを使う。
self.optimizer_encoder = torch.optim.Adam(
self.encoder.parameters(), lr=lr)
最適化手法は元論文よりAdamとしたが、GANではRMSPropのほうがよいという資料もみたので、ここは改善できるポイントかもしれない。
実際には試していないが、各時刻の状態量は2次元以上でも動くように作っているつもり。
train
loss = self.loss_rate_critics[0]*fake_loss - \
self.loss_rate_critics[1]*real_loss + \
self.loss_rate_critics[2]*gp_loss
損失の計算におけるgradient penaltyの比率は、デフォルトでは1:10にしている。これはよく使われている値。
num_criticsによりDiscriminatorを複数回更新後Generatorを更新するやりかたが、この実装でいいのかはやや自信なし。
reconstruct
本物の時系列データ(異常値を含むかもしれない)からGeneratorの入力値となる形式に変換し、その値からGeneratorで元の形式の時系列データを生成するメソッド。
Generatorで生成した各ウインドウの配列から各点の値を求める部分は、
Note that in the preliminary experiments, we found that using the median achieved a better performance than using the mean.
とのことより中央値で算出している。
anomaly_score
元のデータからの距離とCxの出力(本物らしさ)を、zスコアを取った上でいい感じに合成する。
Orionでは四分位数を使ったり絶対値に直したりと色々やっているが、なんでそうしているのかがよくわからなかった。
ここでは元論文の、
Intuitively, the larger RE(x) and the smaller Cx(x) indicate higher anomaly scores.
に従って、zスコアはreconstructed_scoreの場合、
reconstructed_score = np.clip(stats.zscore(reconstructed_score), a_min=0, a_max=None)
スコアがマイナス(元のデータよりも小さい)な部分は0にし、critic_scoreの場合は、
critic_score = np.clip(-stats.zscore(critic_score), a_min=0, a_max=None)
符号を反転させた上でスコアがマイナス(元のデータよりも大きい)な部分は0と、シンプルに実装する。
RE(x)の算出法はpointとdtwのみ対応する。
dtwの計算はライブラリを使ってもよかったが、過去にJavaScriptで実装しているのでそれを転用する。
dtwでは指定したscore_windowの確保ができず算出できない頭とお尻の部分は、scoreを0埋めする。
critic_scoreの算出にKDEを利用してるのは元論文の通り。
動作確認
検証データ
動作検証には telemanom を利用する。
import numpy as np
import pandas as pd
import csv
from .tadgan import ProcessedDataset
def process(src_file, dist_file, window_size=100, step_size=1, train_range=float('inf')):
values = np.load(src_file)[:, 0]
min_value = np.min(values)
max_value = np.max(values)
train_range = min(train_range, len(values))
def normalize(v):
v = v - 0.5 * (max_value + min_value)
if max_value - min_value > 0:
v /= 0.5 * (max_value - min_value)
return v
with open(dist_file, 'w') as f:
writer = csv.writer(f)
writer.writerow(np.append(['i'], [
'i_{}'.format(i) for i in range(window_size)]))
start = 0
end = window_size
while end <= train_range:
writer.writerow(np.append([start], [
normalize(v) for v in values[start:end]]))
start += step_size
end += step_size
class TelemanomDataset(ProcessedDataset):
def __init__(self, processed_csv):
self.df = pd.read_csv(processed_csv)
def __getitem__(self, index):
return (self.df.iloc[index][0], np.array([self.df.iloc[index][1:].values]))
def __len__(self):
return len(self.df)
@property
def window_size(self):
col = len(self.df.columns)
return max(col - 1, 0)
@property
def state_size(self):
return 1
まずprocessでウインドウごとの行に組み替えたcsvを用意する。
zipの取得と解凍は事前に済ませてあるとする。
from tadgan import tadgan, telemanom
train_csv = 'processed_train_A1.csv'
src_file = 'telemanom/data/test/A-1.npy'
label_df = pd.read_csv('telemanom/labeled_anomalies.csv')
anomaly_sequences = eval(label_df[label_df['chan_id'] == 'A-1']['anomaly_sequences'].item())
train_size = sorted(anomaly_sequences, key=lambda x: x[0])[0][0]
telemanom.process(src_file, train_csv, train_range=train_size)
ポイントとしては、src_fileにはtestのデータを使うこと。
train_sizeで異常値とされる値が出てくる手前までのデータを学習用データとする。
TadGANは入力値が(-1,1)の範囲に正規化されている必要があるため、process内でnormalizeしているが、telemanomがそもそも正規化されているので実は不要な処理。

test/A-1.npyをwindow_size=100, step_size=1でcsv化したイメージ
TelemanomDatasetはこれを読み込む用のDatasetで、1次元データなのでstate_sizeは1を返す。
A1
A1を例に実行していく。ハイパーパラメータはすべてデフォルト値。
import numpy as np
import matplotlib.pyplot as plt
train_dataset = telemanom.TelemanomDataset(train_csv)
tadgan.set_seed()
gan = tadgan.TadGAN(train_dataset)
(cx_loss, cz_loss, g_loss) = gan.train(num_epoch=100, debug=True)
cx_lossのグラフを見る。
values = cx_loss
title = 'cx_loss'
start = 0
end = values.shape[0]
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111)
ax.set_title(title)
x = np.linspace(start, end, end - start)
ax.plot(x,values[start:end])
plt.show()
エポックが100程度であればGPUなら数分で終わる
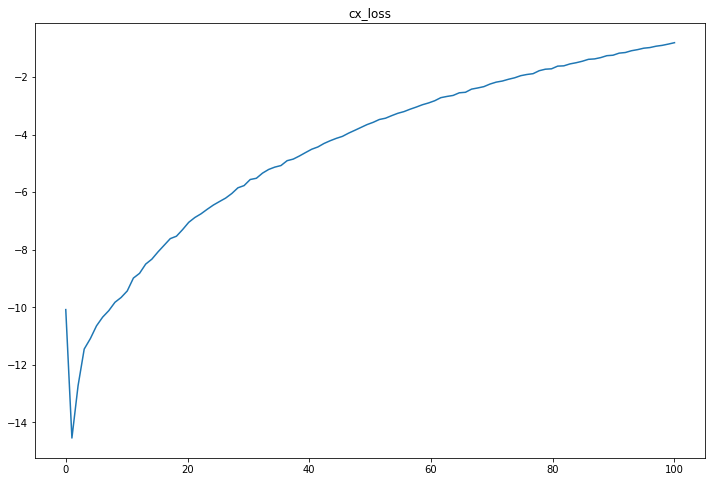
cx_lossの値は大きくなるほどよいので、順調に改善している様子がわかる。
同様にg_lossのグラフを見る。
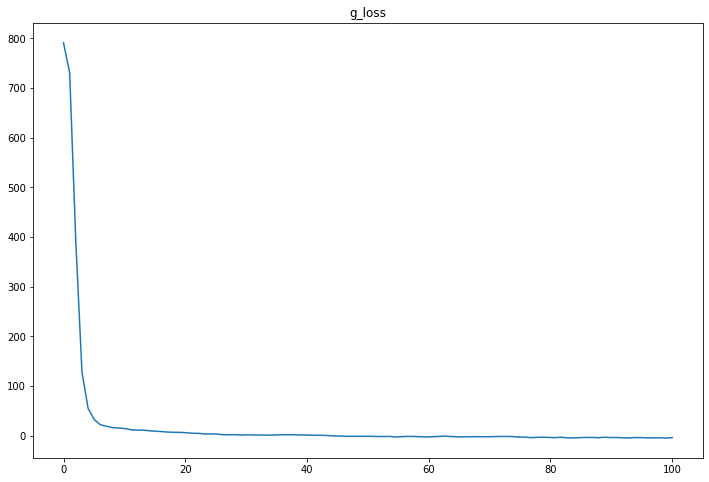
g_lossの値は小さくなるほどよいが、早々サチっており、学習は十分できている様子。
raw = gan.raw
reconstructed = gan.reconstruct(raw)
start = 0
end = raw.shape[0]
title = 'train'
fig = plt.figure(figsize=(8, 4))
ax = fig.add_subplot(111)
x = np.linspace(start, end, end - start)
ax.set_title(title)
for [anomaly_start, anomaly_end] in anomaly_sequences:
ax.axvspan(anomaly_start, anomaly_end, color='gray', alpha=0.25)
ax.plot(raw, 'r', label='raw')
ax.plot(reconstructed, 'b', label='reconstructed')
plt.xlim(start, end)
plt.ylim(-1.1, 1.1)
ax.legend()
plt.show()

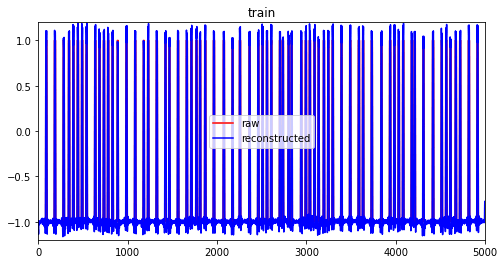
学習データと学習データから再生成した値を比較する。
A1のデータは1が正常値で、学習データはすべて1となっている。
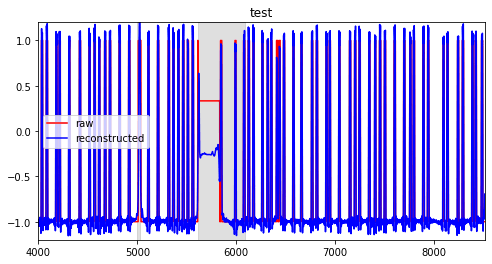
次は検証用のエラーを含む範囲のデータとそれから再生成した値を表示する。
left_edge = int(train_size*0.8)
test_values =np.load(src_file)[left_edge:-1,0].reshape(-1, 1)
test_reconstructed = gan.reconstruct(test_values)
title = 'test'
start = left_edge
end = left_edge + test_values.shape[0]
fig = plt.figure(figsize=(8, 4))
ax = fig.add_subplot(111)
ax.set_title(title)
x = np.linspace(start, end - 1, test_values.shape[0])
for [anomaly_start, anomaly_end] in anomaly_sequences:
ax.axvspan(anomaly_start, anomaly_end, color='gray', alpha=0.25)
ax.plot(x, test_values, 'r', label='raw')
ax.plot(x, test_reconstructed, 'b', label='reconstructed')
plt.xlim(start, end)
plt.ylim(-1.1, 1.1)
ax.legend()
plt.show()

異常値の範囲は[[4690, 4774]]でグラフ中では薄灰色の帯で表示している。
これを元にanomaly_scoreを計算する。
まずは、距離はpoint、critic_scoreは利用しない形式で算出する。
values = gan.anomaly_score(test_values, test_reconstructed, distance='point', alpha=1)
title = 'distance=point'
start = left_edge
end = left_edge + test_values.shape[0]
fig = plt.figure(figsize=(8, 4))
ax = fig.add_subplot(111)
ax.set_title(title)
x = np.linspace(start, end - 1, test_values.shape[0])
for [anomaly_start, anomaly_end] in anomaly_sequences:
ax.axvspan(anomaly_start, anomaly_end, color='gray', alpha=0.25)
ax.plot(x, values, 'b', label='reconstructed')
plt.xlim(start, end)
plt.ylim(bottom=0)
ax.legend()
plt.show()

異常値の範囲でピーンとスコアが立っている。
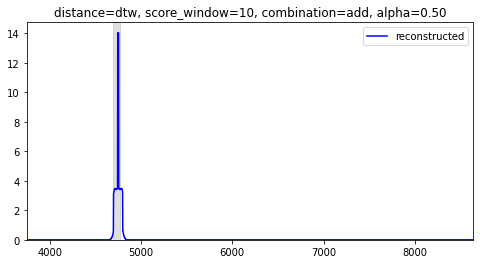
同様に距離はdtw、critic_scoreは利用しない形式で算出する。
values = gan.anomaly_score(test_values, test_reconstructed, distance='dtw', alpha=1)

こちらもいい感じに異常値の範囲だけでスコアがあがっている。
参考にcritic_scoreだけをグラフにしてみる。
values = gan.anomaly_score(test_values, test_reconstructed, distance='point', alpha=0)

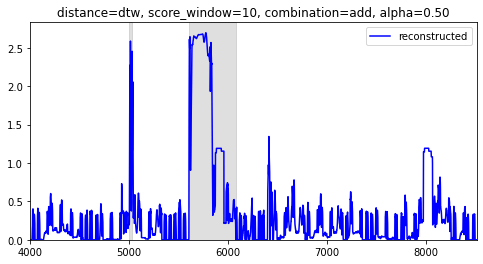
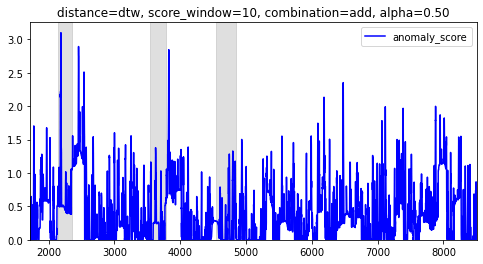
最後に距離はdtw、critic_scoreを加算(比率は1:1)する形式で算出する。
values = gan.anomaly_score(test_values, test_reconstructed, distance='dtw', alpha=0.5)
加算方式では、Zスコアなのでスコアが3を超えていたら異常値とシンプルに判断して良いだろう。
A1は実に単調なデータだったため、あまり面白みはない結果となったが、きちんと異常値の範囲を検出できている。
A2


学習データと学習データから再生成した値を比較する。

検証用のエラーを含む範囲のデータとそれから再生成した値を比較する。

ピークに追随しきれていないのでもう少し学習させてもいいかもしれない。
各スコアを算出


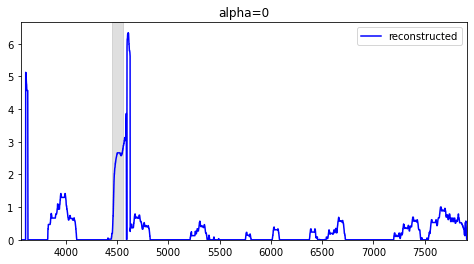

A1と比べて変化の激しいデータだが、きちんと異常値の範囲を検出できている。
T1

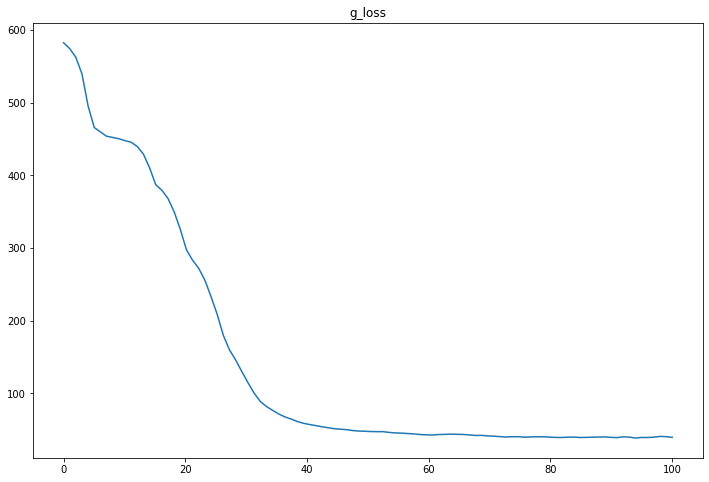

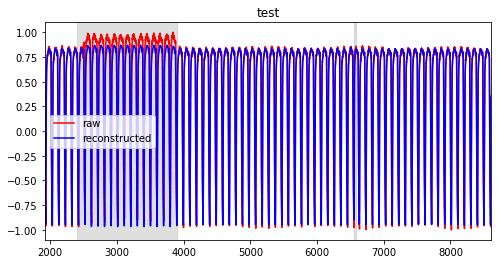

スコアは上がっているが、[2399, 3898]の範囲はやや低め。
E1

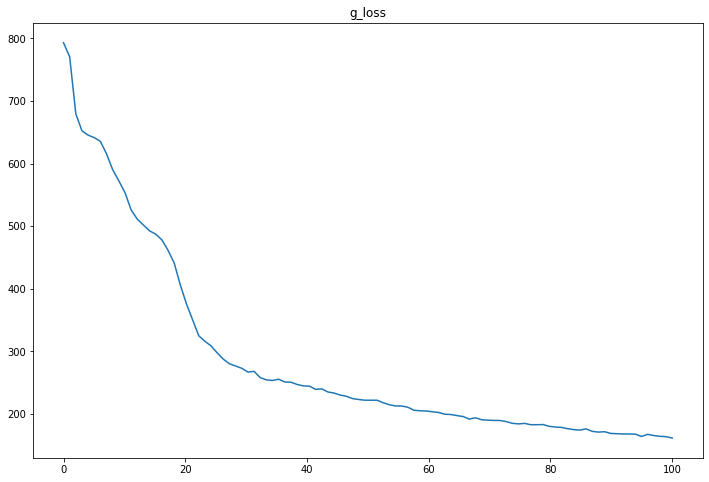
再生成した値が[-1, 1]の範囲を超えてしまっている。
g_lossがまだサチってないのでもう少し学習させたほうがいいのかもしれない。

P1
ピークに十分追随させるためエポックを500で実行する。




[2149, 2349], [3539, 3779]の範囲はスコアがあがっているが、[4536, 4844]の範囲はさっぱり。エラーらしき値をしっかり再生成できてしまっている。
まとめ
いい感じにPyTorchで動くTadGANが実装できたが、当たり前の話ですべてのデータでうまくいくわけではない。
ハイパーパラメータの調整や、スコアのスムージングなど工夫の余地が残っている。
あとは2022年で最新の時系列データのディープラーニング手法が知りたい。
Discussion