衛星のあれこれを地図上に描画する
衛星のあれこれを地図上に描画するには、三次元の地心座標系を経度緯度の地理座標系に直すためいろいろ工夫をしなければいけない。
SystemsToolKit[1]等を使えばそのあたりの苦労もなく描画できるが、JavaScript(TypeScript)で実現したいので必要な工夫点をひとつひとつ整理して自前実装していく。
直下点(Nadir)
ある時刻における、衛星の位置の直下点の経度緯度を求める。
衛星の軌道の諸元はTwo Line Elements(TLE)から得る。
時刻と軌道から位置を求めるアルゴリズムはsgp4が有名だ。
さすがにsgp4をイチからコードに書き起こすのは大変なので、ここだけはライブラリを利用させてもらう。
今回はTypeScript対応もしているsatellite.jsを利用する。
import type {
Position,
} from "geojson";
import {
propagate, gstime, twoline2satrec,
eciToGeodetic, degreesLong, degreesLat, PositionAndVelocity
} from "satellite.js";
const _getNadir = (positionAndVelocity: PositionAndVelocity, gmst: number): Position => {
if (typeof positionAndVelocity.position === "boolean") {
throw TypeError("positionAndVelocity has not a number.");
}
const position = eciToGeodetic(
positionAndVelocity.position,
gmst
);
return [
degreesLong(position.longitude),
degreesLat(position.latitude),
];
}
const nadir = (tleLine1: string, tleLine2: string, date: Date): Position => {
const satrec = twoline2satrec(tleLine1, tleLine2);
const positionAndVelocity = propagate(satrec, date);
const gmst = gstime(date);
return _getNadir(positionAndVelocity, gmst);
}
satellite.jsを利用するだけで、特に特別な工夫もなく経度緯度を求めることができる。
衛星の軌跡(Sub-satellite Track)
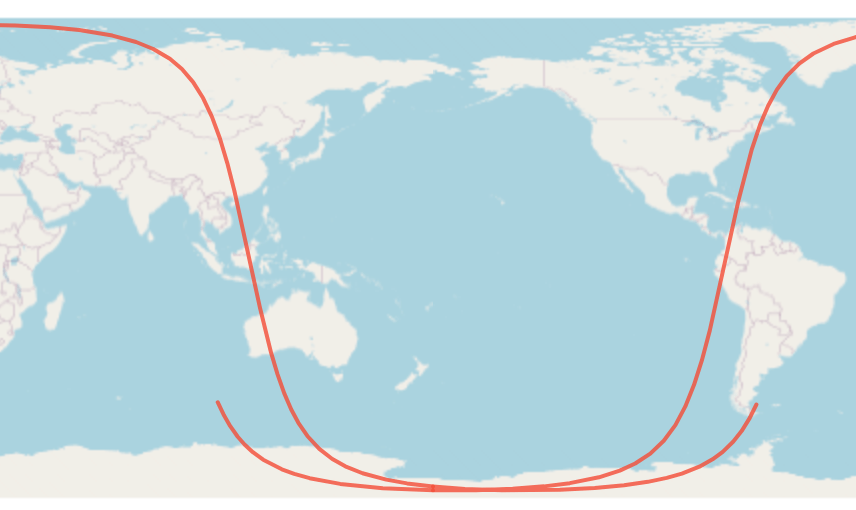
衛星の軌跡を地上に投影したものをSub-satellite Trackという。
TLEと開始時刻、終了時刻から計算するメソッドを考える。
このとき時刻をどの刻み幅(dt)で計算を進めるかだが、dtを直接引数として指定するとなると衛星ごとに適切な秒数を使う人間が考えなければならない。
それも面倒なので、今回は分割数(split)で衛星ごとの周回時間を割った値をdtとする方針で実装する。とはいえ、今回のアルゴリズムでは前後の点の経度差が180deg以下になるくらい十分小さくなければ計算が破綻するし、点の間の経度差がある程度以上細かくなければきれいな曲線は描けない。衛星の地表との相対速度にあわせて分割数の調整も必要となるため、面倒さから完全に解放されるわけではない。
デフォルト値としてsplit=360としているが、低軌道ではこれくらい分割しないと曲線がきれいに描けなかった。
const subSatelliteTrack = (
tleLine1: string,
tleLine2: string,
start: Date,
end: Date,
userOptions?: {
split?: number;
}): number[][] => {
const options = Object.assign(
{
split: 360,
},
userOptions
);
const satrec = twoline2satrec(tleLine1, tleLine2);
const meanMotion = satrec.no; // [rad/min]
const orbitPeriod = (2 * Math.PI) / (meanMotion / 60); // [sec]
const dt = orbitPeriod / options.split;
const tracks: Position[][] = [[]];
let linestringIndex = 0;
const d = new Date(start.getTime());
while (d < end) {
const positionAndVelocity = propagate(satrec, d);
if (typeof positionAndVelocity.position === "boolean") {
throw TypeError("positionAndVelocity has not a number.");
}
const gmst = gstime(d);
const current = _getNadir(positionAndVelocity, gmst);
if (tracks[linestringIndex].length > 0) {
const before =
tracks[linestringIndex][tracks[linestringIndex].length - 1];
if (Math.abs(current[0] - before[0]) > 180) {
if (current[0] < 0 && before[0] > 0) {
const lat =
((current[1] - before[1]) / (360 + current[0] - before[0])) *
(180 - before[0]) +
before[1];
tracks[linestringIndex].push([180, lat]);
tracks[++linestringIndex] = [[-180, lat]];
}
if (current[0] > 0 && before[0] < 0) {
const lat =
((current[1] - before[1]) / (-360 + current[0] - before[0])) *
(-180 - before[0]) +
before[1];
tracks[linestringIndex].push([-180, lat]);
tracks[++linestringIndex] = [[180, lat]];
}
}
}
tracks[linestringIndex].push(current);
d.setSeconds(d.getSeconds() + dt);
}
return track;
}
+-180度線をまたぐところでlineStringを分割して経度を+-180の範囲に丸めてあげているところが工夫点。これをしないと地球は丸いため値が発散してしまう。
そのため返り値はlineStringの配列となる。
観測方向の地表面との交点
ある時刻における、衛星の位置と観測方向、今回は軌道座標系(LVLH座標系)における観測方向ベクトルから、観測点(観測方向ベクトルが地表面と交錯する点)の座標(地心座標系)を幾何学的に求める。

import {
..., // 省略
EciVec3
} from "satellite.js";
const getGroundObservingPosition = (
satellitePosition: EciVec3<number>,
observeDirection: EciVec3<number>,
a: number, // 回転楕円体の長半径
b: number, // 回転楕円体の短半径
ex: EciVec3<number>,
ey: EciVec3<number>,
ez: EciVec3<number>
): EciVec3<number> => {
const c = a;
const d = {
x: dot({ x: ex.x, y: ey.x, z: ez.x }, observeDirection),
y: dot(
{ x: ex.y, y: ey.y, z: ez.y }, observeDirection),
z: dot(
{ x: ex.z, y: ey.z, z: ez.z }, observeDirection),
};
const A = d.x ** 2 / a ** 2 + d.y ** 2 / b ** 2 + d.z ** 2 / c ** 2;
const B =
(2 * d.x * satellitePosition.x) / a ** 2 +
(2 * d.y * satellitePosition.y) / b ** 2 +
(2 * d.z * satellitePosition.z) / c ** 2;
const C =
satellitePosition.x ** 2 / a ** 2 + satellitePosition.y ** 2 / b ** 2 + satellitePosition.z ** 2 / c ** 2 - 1;
const D = B ** 2 - 4 * A * C;
const t1 = (-B + Math.sqrt(D)) / (2 * A);
const t2 = (-B - Math.sqrt(D)) / (2 * A);
if (isNaN(t1) || isNaN(t2)) throw new Error();
const P1 = add(
satellitePosition,
multiple(d, t1)
);
const P2 = add(
satellitePosition,
multiple(d, t2)
);
return t1 > t2 ? P2 : P1;
};
ex, ey, ezは軌道座標系(LVLH座標系)の方位ベクトル(進行方向、軌道面外方向、地心方向)で以下のように求める。
const ex = unit(positionAndVelocity.velocity);
const ez = unit(multiple(positionAndVelocity.position, -1));
const ey = unit(
cross(
ez,
ex,
)
);
add, multiple, dot, cross, norm, unitはベクトルの基本的な計算のためのメソッドなので記述は割愛。
まったく当てずっぽうな方向で無い限り、方位ベクトルを延長すると回転楕円体と2点で交わるはずで、そのうち衛星に近いほうが観測点となる。
その瞬間の観測範囲(Footprint)
仮想的なセンサーのField of view (fov)の範囲に収まる地表面の範囲を求める。
観測範囲は矩形を想定し、fovを進行方向と直交方向の角度で与える。
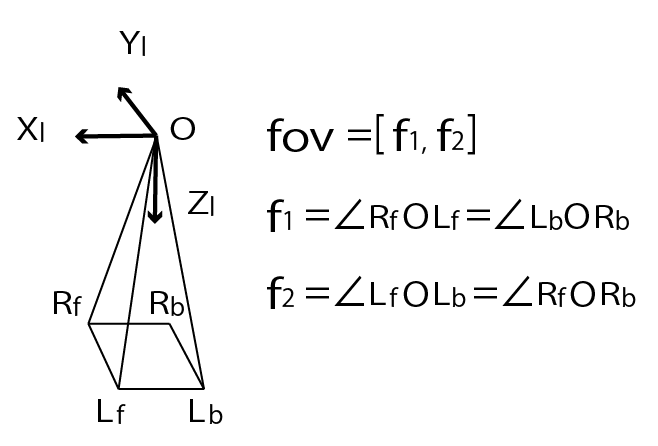
fovから矩形の四隅を求め、かつ各辺にはinsert分の点を挿入する。
insert=0(等角航路)でもよいのだが、極に近いと本来の曲線(大圏航路)と差が大きくなってしまう[2]ため、ある程度は挿入することをおすすめする(デフォルトは5)。
import {
..., // 省略
GeodeticLocation
} from "satellite.js";
const toLonLat = (point: GeodeticLocation, reference?: number[]): number[] => {
let lon = degreesLong(point.longitude);
if (reference && Math.abs(reference[0] - lon) >= 180) {
if (reference[0] >= 0) lon += 360;
else lon -= 360;
}
return [lon, degreesLat(point.latitude)];
}
interface FootprintOptions {
insert?: number;
fov?: number[]; // [along track, cross track] [deg]
a?: number; // 回転楕円体の超半径[km]
f?: number; // 扁平率
}
const _getFootprint = (
positionAndVelocity: PositionAndVelocity,
gmst: number,
userOptions?: FootprintOptions): Points => {
const options = Object.assign(
{
insert: 5,
fov: [30, 30],
a: 6378.137, // WGS84
f: 1 / 298.257223563 // WGS84
},
userOptions
);
if (typeof positionAndVelocity.position === "boolean" || typeof positionAndVelocity.velocity === "boolean") {
throw TypeError("positionAndVelocity has not a number.");
}
const center = _getNadir(positionAndVelocity, gmst);
const [f1, f2] = [(options.fov[0] / 2 * Math.PI) / 180, (options.fov[1] / 2 * Math.PI) / 180];
const f3 = Math.atan(Math.sqrt(Math.tan(f1) ** 2 + Math.tan(f2) ** 2));
const f4 = Math.atan(Math.tan(f1) / Math.tan(f2));
const rf = {
x: Math.sin(f3) * Math.cos(f4),
y: Math.sin(f3) * Math.sin(f4),
z: Math.cos(f3),
};
const lf = {
x: Math.sin(f3) * Math.cos(f4),
y: -Math.sin(f3) * Math.sin(f4),
z: Math.cos(f3),
};
const lb = {
x: - Math.sin(f3) * Math.cos(f4),
y: -Math.sin(f3) * Math.sin(f4),
z: Math.cos(f3),
};
const rb = {
x: -Math.sin(f3) * Math.cos(f4),
y: Math.sin(f3) * Math.sin(f4),
z: Math.cos(f3),
};
const length = options.insert + 1;
const ex = unit(positionAndVelocity.velocity);
const ez = unit(multiple(positionAndVelocity.position, -1));
const ey = unit(
cross(
ez,
ex,
)
);
const a = options.a;
const b = a * (1 - options.f);
const positions = [
getGroundObservingPosition(positionAndVelocity.position, rf, a, b, ex, ey, ez),
getGroundObservingPosition(positionAndVelocity.position, lf, a, b, ex, ey, ez),
getGroundObservingPosition(positionAndVelocity.position, lb, a, b, ex, ey, ez),
getGroundObservingPosition(positionAndVelocity.position, rb, a, b, ex, ey, ez),
];
if (within([0, 0], [...positions.map((position) => [
position.x, position.y
]), [positions[0].x, positions[0].y]], { includeBorder: true })) {
return _transformEnclosingPoleRing(
[...positions, positions[0]].map((p) => toLonLat(eciToGeodetic(
p,
gmst
), center)),
"EPSG:4326",
options.insert,
positionAndVelocity.position.z >= 0
);
}
// right front to left front
{
const direction = { ...rf };
for (let i = 1; i < length; i++) {
direction.y += -(2 * Math.sin(f3) * Math.sin(f4)) / length;
positions.splice(i, 0, getGroundObservingPosition(positionAndVelocity.position, direction, a, b, ex, ey, ez));
}
}
// left front to left back
{
const direction = { ...lf };
for (let i = 1; i < length; i++) {
direction.x += -(2 * Math.sin(f3) * Math.cos(f4)) / length;
positions.splice(i + length, 0, getGroundObservingPosition(positionAndVelocity.position, direction, a, b, ex, ey, ez));
}
}
// left back to right back
{
const direction = { ...lb };
for (let i = 1; i < length; i++) {
direction.y += (2 * Math.sin(f3) * Math.sin(f4)) / length;
positions.splice(i + length * 2, 0, getGroundObservingPosition(positionAndVelocity.position, direction, a, b, ex, ey, ez));
}
}
// right back to right front
{
const direction = { ...rb };
for (let i = 1; i < length; i++) {
direction.x += (2 * Math.sin(f3) * Math.cos(f4)) / length;
positions.splice(i + length * 3, 0, getGroundObservingPosition(positionAndVelocity.position, direction, a, b, ex, ey, ez));
}
}
const lonlats = positions.map((position) => {
return toLonLat(eciToGeodetic(position, gmst), center);
});
return [...lonlats, lonlats[0]];
}
const footprint = (tleLine1: string, tleLine2: string, date: Date, userOptions?: FootprintOptions): Points => {
const satrec = twoline2satrec(tleLine1, tleLine2);
const positionAndVelocity = propagate(satrec, date);
const gmst = gstime(date);
return _getFootprint(positionAndVelocity, gmst, userOptions);
};
GeoJSONにすることを見越して、点の並びが反時計回りとなるよう、右前->左前->左後->右後の順に計算を進めている。
eciToGeodeticは地心座標系の点を経度緯度に変換するが、このとき経度を-180から180度の間に収めてしまう。
フットプリントが+-180度線をまたぐ場合に図形が崩れてしまうため、toLonLatでは基準点を元に補正している。
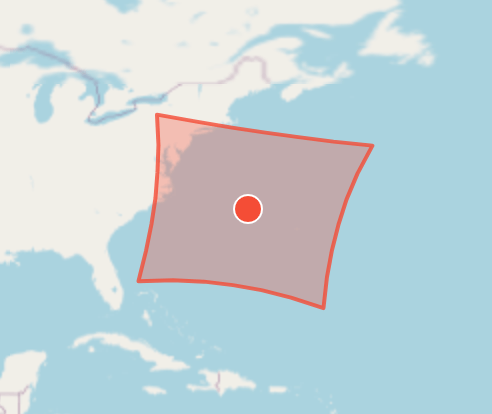
なお、フットプリントが極点を囲む場合は特殊な処理が必要で、その中身はtransformEnclosingPoleRingにまとめてあるのでここでは説明を割愛する。
極点を囲んでいるかの判定をするwithinも同様に割愛。
衛星の姿勢(ロール、ピッチ)を指定できるようになるとよいが、それは後日の課題とする。
撮像可能範囲(AccessArea)
衛星の撮像可能な範囲を地上に投影した帯をAccess Areaという。
TLEと開始時刻、終了時刻から計算するメソッドを考える。
進行方向に対して左右に何度傾けることができるか、を引数rollとして設定できるようにする。
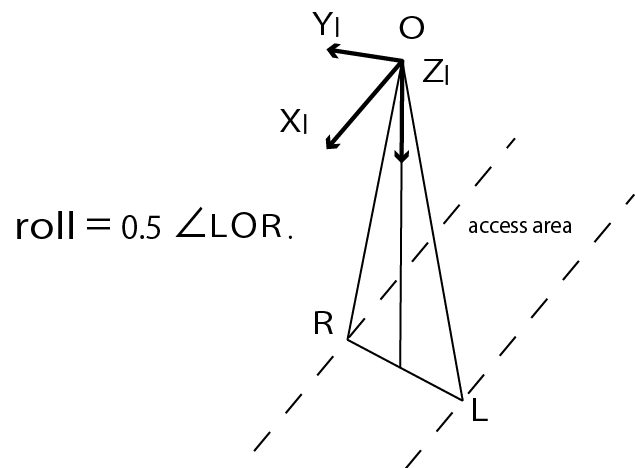
interface AccessAreaOptions {
split?: number;
roll?: number; // [deg]
a?: number; // [km]
f?: number;
insert?: number;
}
const _getEdge = (
satellitePosition: EciVec3<number>,
gmst: number,
a: number,
b: number,
ex: EciVec3<number>,
ey: EciVec3<number>,
ez: EciVec3<number>,
f3: number,
insert: number,
reference: number[],
start: boolean
): Points => {
const edgePositions: Points = [];
const direction = start ? 1 : -1;
const length = insert + 1;
for (let i = 1; i < length; i++) {
const theta = direction * (f3 - (i * 2 * f3) / length);
edgePositions.push(
toLonLat(
eciToGeodetic(
getGroundObservingPosition(
satellitePosition,
{
x: 0,
y: Math.sin(theta),
z: Math.cos(theta),
},
a,
b,
ex,
ey,
ez
),
gmst
),
reference
)
);
}
return edgePositions;
};
export const accessArea = (
tleLine1: string,
tleLine2: string,
start: Date,
end: Date,
userOptions?: AccessAreaOptions
): Points[] => {
const options = Object.assign(
{
split: 360,
roll: 10,
radius: 6378.137, // WGS84
f: 1 / 298.257223563, // WGS84
insert: 5,
},
userOptions
);
const satrec = twoline2satrec(tleLine1, tleLine2);
const meanMotion = satrec.no; // [rad/min]
const orbitPeriod = (2 * Math.PI) / (meanMotion / 60); // [sec]
const dt = orbitPeriod / options.split;
const f3 = (options.roll * Math.PI) / 180;
let leftVectors: EciVec3<number>[] = [];
let rightVectors: EciVec3<number>[] = [];
let startEdgePositions: Points = [];
let leftPositions: Points = [];
let rightPositions: Points = [];
let onboardIndex = 0;
let across = 0;
let reference: Position | null = null;
let leftTrack: Points = [];
let rightTrack: Points = [];
const linearRings: Points[] = [];
const d = new Date(start.getTime());
while (d < end) {
const positionAndVelocity = propagate(satrec, d);
if (
typeof positionAndVelocity.position === "boolean" ||
typeof positionAndVelocity.velocity === "boolean"
) {
throw TypeError("positionAndVelocity has not a number.");
}
const gmst = gstime(d);
const ex = unit(positionAndVelocity.velocity);
const ez = unit(multiple(positionAndVelocity.position, -1));
const ey = unit(
cross(
ez,
ex,
)
);
const a = options.radius;
const b = a * (1 - options.f);
const leftVector = getGroundObservingPosition(
positionAndVelocity.position,
{
x: 0,
y: Math.sin(-f3),
z: Math.cos(f3),
},
a,
b,
ex,
ey,
ez
);
const leftLocation = eciToGeodetic(leftVector, gmst);
const rightVector = getGroundObservingPosition(
positionAndVelocity.position,
{
x: 0,
y: Math.sin(f3),
z: Math.cos(f3),
},
a,
b,
ex,
ey,
ez
);
const rightLocation = eciToGeodetic(rightVector, gmst);
if (!reference) {
reference = _getNadir(positionAndVelocity, gmst);
startEdgePositions = _getEdge(
positionAndVelocity.position,
gmst,
a,
b,
ex,
ey,
ez,
f3,
options.insert,
reference,
true
);
}
const left = toLonLat(leftLocation, reference);
const right = toLonLat(rightLocation, reference);
if (across === 0) {
if ((180 - Math.abs(left[0])) * (180 - Math.abs(right[0])) < 0)
across = 1;
} else if (across === 1) {
if ((180 - Math.abs(left[0])) * (180 - Math.abs(right[0])) > 0)
across = -1;
}
leftVectors.push(leftVector);
rightVectors.push(rightVector);
leftPositions.push(left);
rightPositions.push(right);
onboardIndex++;
if (onboardIndex > 1) {
const vectorRing = [
...rightVectors,
...[...leftVectors].reverse(),
rightVectors[0],
];
if (
within(
[0, 0],
vectorRing.map((v) => [v.x, v.y])
)
) {
leftTrack = leftTrack.concat(
leftPositions.slice(0, leftPositions.length - 1)
);
rightTrack = rightTrack.concat(
rightPositions.slice(0, rightPositions.length - 1)
);
const middleLeftPosition = [...leftPositions[leftPositions.length - 1]];
const middleRightPosition = [
...rightPositions[rightPositions.length - 1],
];
if (
Math.abs(middleLeftPosition[0] - leftTrack[leftTrack.length - 1][0]) >
180
) {
middleLeftPosition[0] +=
leftTrack[leftTrack.length - 1][0] > 0 ? 360 : -360;
}
if (
Math.abs(
middleRightPosition[0] - rightTrack[rightTrack.length - 1][0]
) > 180
) {
middleRightPosition[0] +=
rightTrack[rightTrack.length - 1][0] > 0 ? 360 : -360;
}
leftTrack.push(middleLeftPosition);
rightTrack.push(middleRightPosition);
const polarLat = positionAndVelocity.position.z >= 0 ? 90 : -90;
leftTrack.push([middleLeftPosition[0], polarLat]);
rightTrack.push([middleRightPosition[0], polarLat]);
linearRings.push([
leftTrack[0],
...startEdgePositions,
...rightTrack,
...[...leftTrack].reverse(),
]);
leftVectors = [leftVector];
rightVectors = [rightVector];
reference = _getNadir(positionAndVelocity, gmst);
const left = toLonLat(leftLocation, reference);
leftPositions = [left];
const right = toLonLat(rightLocation, reference);
rightPositions = [right];
onboardIndex = 1;
across =
(180 - Math.abs(left[0])) * (180 - Math.abs(right[0])) < 0 ? 1 : 0;
leftTrack = [[left[0], polarLat]];
rightTrack = [[right[0], polarLat]];
startEdgePositions = [];
} else if (across < 1) {
const current = _getNadir(positionAndVelocity, gmst);
if (across === 0) {
if (Math.abs(current[0] - reference[0]) >= 180) {
across = -1;
} else {
leftTrack.push(leftPositions[0]);
rightTrack.push(rightPositions[0]);
}
}
if (across < 0) {
leftTrack = leftTrack.concat(leftPositions);
rightTrack = rightTrack.concat(rightPositions);
let linearRing = [leftTrack[0], ...startEdgePositions, ...rightTrack];
const endeEdgePositions = (startEdgePositions = _getEdge(
positionAndVelocity.position,
gmst,
a,
b,
ex,
ey,
ez,
f3,
options.insert,
reference,
false
));
linearRing = linearRing.concat([
...endeEdgePositions,
...[...leftTrack].reverse(),
]);
linearRings.push(linearRing);
rightTrack = [];
leftTrack = [];
}
leftVectors = [leftVector];
rightVectors = [rightVector];
reference = current;
leftPositions = [toLonLat(leftLocation, reference)];
rightPositions = [toLonLat(rightLocation, reference)];
onboardIndex = 1;
if (across < 0) {
startEdgePositions = startEdgePositions = _getEdge(
positionAndVelocity.position,
gmst,
a,
b,
ex,
ey,
ez,
f3,
options.insert,
reference,
true
);
}
across = 0;
}
}
d.setSeconds(d.getSeconds() + dt);
if (end <= d) {
leftTrack = leftTrack.concat(leftPositions);
rightTrack = rightTrack.concat(rightPositions);
if (leftTrack.length > 1 && rightTrack.length > 1) {
let linearRing = [leftTrack[0], ...startEdgePositions, ...rightTrack];
const endEdgePositions = _getEdge(
positionAndVelocity.position,
gmst,
a,
b,
ex,
ey,
ez,
f3,
options.insert,
reference,
false
);
linearRing = linearRing.concat([
...endEdgePositions,
...[...leftTrack].reverse(),
]);
linearRings.push(linearRing);
}
}
}
return linearRings;
};
捜査線(left to right)が+-180度線をまたいでない場合は、直前の点をストックする。
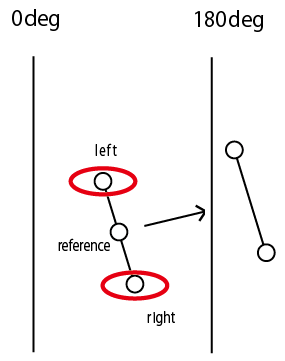
これを+-180度線をまたぎきるまで続ける。
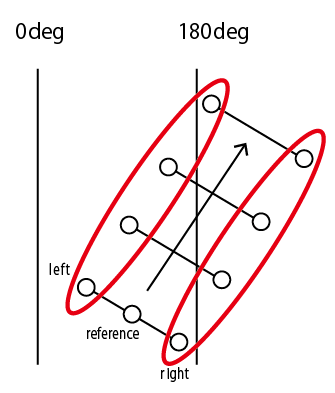
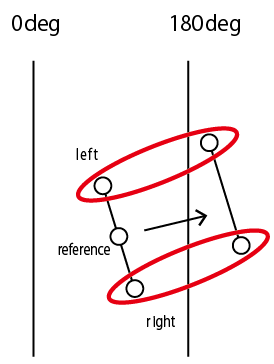
またぎ終えたらストックした点をつなぎLinear Ringを作り、ストックをリセットして次の探索に進む。
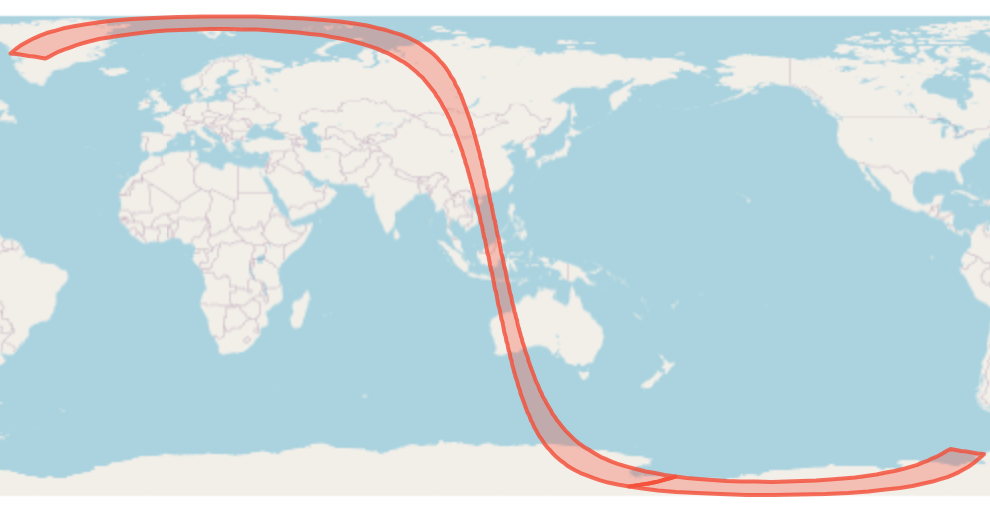
極点を含む場合はやはり特殊な処理が必要で、中点を求めてポリゴンを分割する。
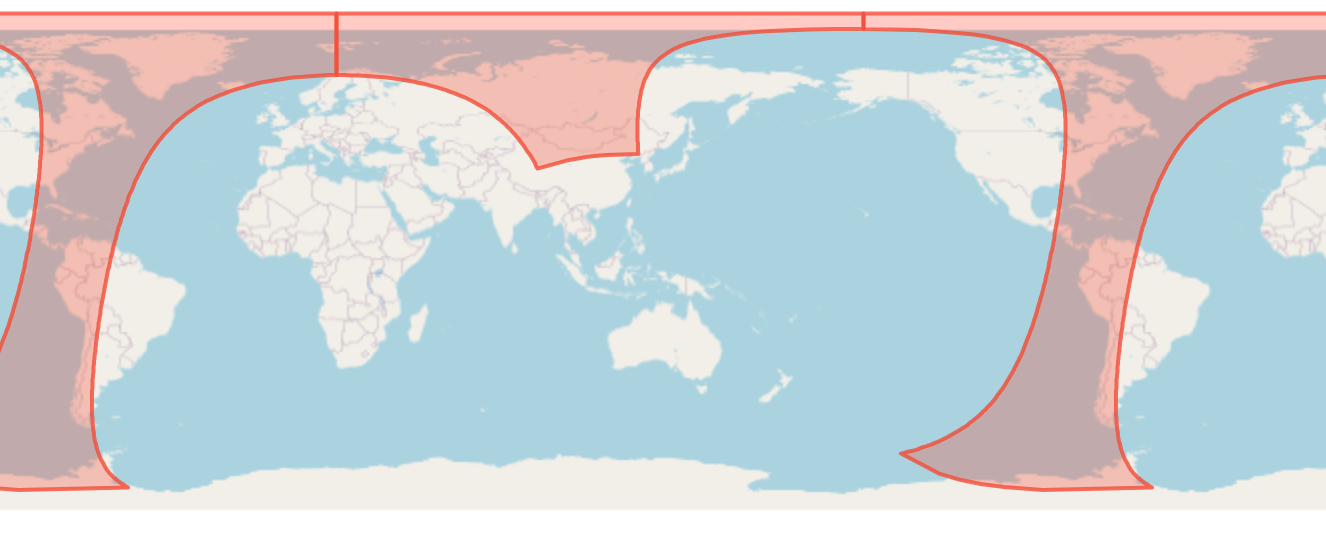
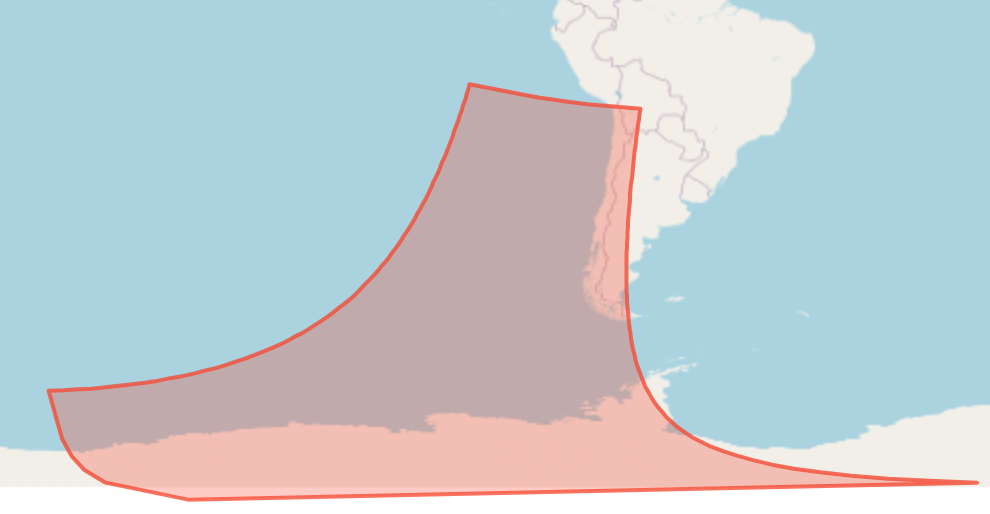
また、左右の軌跡を単純につなげるだけでは、極に近い場合ポリゴンが崩れてしまう(自己交差してしまう)。

よって左右をつなぐ辺はinsert分だけ点を挿入することで交錯が発生しないようにしている。
このあたりの処理は_getEdgeにまとめている。
まとめ
よほど複雑な条件でない限りは、衛星のあれこれを地図上に描画する需要はほぼこれで満たせるはずである。
各メソッドの返り値をGeoJSON化すれば地図上へすぐに表示できるだろう。
コードはgeo4326にまとめてある。
工夫した点の大体は180線に起因する処理で地球がまるくなければよかったのにと何度も思った。
Discussion