線形対数計算量（O(n log n)）の直観的な説明

線形探索の計算量は$O(n)$、二次計算量は$O(n^2)$で表され、これらは比較的理解しやすいものです。しかし、merge sortのような分割統治法を用いるアルゴリズムでは、計算量が$O(n \log n)$となり、少し戸惑うかもしれません。というか、私は戸惑いました。テキストベースで説明するよりも直観的に理解しやすいように簡単な例と図をを使って説明したいと思います。

log n の部分

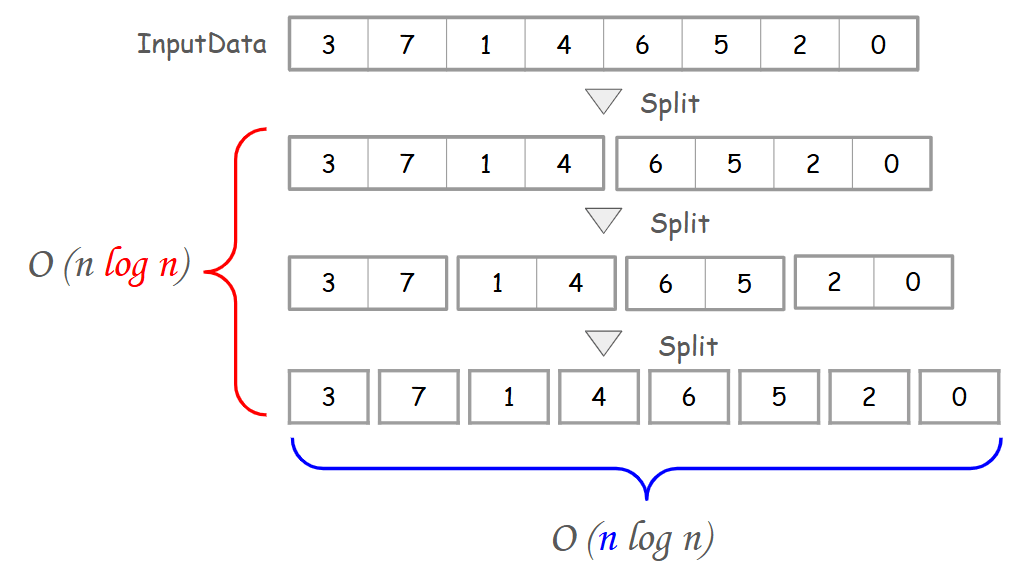
まず、'log n' は、データを小さく分割していき、最終的に2つの要素がペアになるまでの分割回数を示しています。merge sortやquick sortなど、分割統治法を使ったアルゴリズムでは、データをどんどん分割しながら小さな問題に分解します。上記の図では、8つのデータを3回分割しているため、$log(8)=3$となります。つまり3階層分ですね。

n の部分

次に、nは各分割段階で走査するデータの個数を示します。各段階でn個の要素を処理するため、階層レベルで線形の作業が必要となります。

まとめ

このように、分割統治法を使うアルゴリズムの計算量が$O(n \log n)$になる理由は、log n の分割回数と n の走査量を掛け合わせて考えることで、直感的に理解できます。この図を参考にすると、分割統治法の計算量を理解しやすくなるかと思います。初歩的な内容ではありますが、どなたかの一助になれば幸いです。