モンテカルロ法を使って円周率を求めてみた(Python)

概要

モンテカルロ法を使って円周率(3.14159265...)を求めていきます。

モンテカルロ法とは

モンテカルロ法は、確率的な手法の一つで、ランダムなサンプリングを用いて、数学的な問題を解決する手法です。具体的には、乱数を用いて問題の解候補を生成し、それらの解候補に基づいて問題の解を近似的に求めます。

モンテカルロ法で円周率を求める手順

半径1の円内にランダムに点を打ち、その点のうち円内に入るものの割合を計算することで円周率を求めることができます。これは、円周率と円の面積の関係から導かれる式「円の面積＝πr²」を利用する方法です。

以下の手順で円周率を求めることができます。

1. 正方形の中に、半径1の円を描きます。
2. 正方形の中にランダムに点を打ちます。
3. 点が円内に入る場合はカウントします。
4. 点の総数をカウントします。
5. 円内に入った点の割合を計算します。
6. 円周率は、円内に入った点の割合に4を掛けた値として求めることができます。

このように、ランダムなサンプリングを用いることで、円周率を近似的に求めることができます。サンプル数を増やすことで、より正確な値を求めることができます。

シンプルな実装

import numpy as np
from numpy import random
import matplotlib.pyplot as plt

TRIALS = 100 # 試行回数

x_list = [random.uniform(0, 1) for i in range(TRIALS)]
y_list = [random.uniform(0, 1) for i in range(TRIALS)]

# √x^2 + y^2が原点からの距離なのでそれが1より大きいか小さいかで判断
points = np.hypot(x_list, y_list)
count = 0
for i in points:
    if i <= 1:
        count += 1

my_pie = (count / TRIALS) * 4.0
print(f"{my_pie}")
plt.plot(x_list, y_list, '.')

# x^2 + y^2 = 1の式を使って円の第1象限を記述
x_pi = [i for i in np.arange(0.0, 1.01, 0.01)]
y_pi = np.sqrt(1 - np.square(x_pi))  # y = √1-x^2

plt.plot(x_pi, y_pi)
plt.xlim(0., 1.)
plt.ylim(0., 1.)
plt.xlabel("x")
plt.ylabel("y")
plt.title("Monte Carlo method")

plt.show()

結果:
3.36

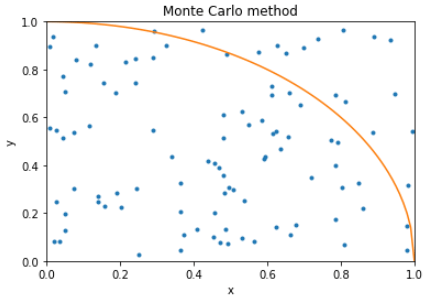
3.14には程遠いですね。
では次に1000000回プロットしてみましょう。
TRIALS = 100をTRIALS = 1000000に書き換えてください。

結果:
3.142128

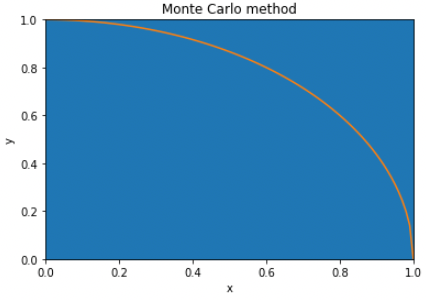
さすがに1000000ともなれば散布図が真っ青ですね...
出力結果も3.142128と円周率に近似しておりたしかにモンテカルロ法で円周率が求められそうです。

モンテカルロ法の途中経過を見てみる

先ほどの円周率を計算するコードを関数化して、途中経過をリストに格納しグラフを作成してみます。

倍率はMAGNIFICATIONで、
試行回数はTRIALSで設定します。

import numpy as np
from numpy import random
import matplotlib.pyplot as plt
import math


def ft_pi(trials):
    x_list = [random.uniform(0, 1) for i in range(trials)]
    y_list = [random.uniform(0, 1) for i in range(trials)]
    
    points = np.hypot(x_list, y_list)  # √x^2 + y^2
    
    count = 0
    for i in points:
        if i <= 1:
            count += 1
    
    my_pie = (count / trials) * 4.0
    return my_pie

MAGNIFICATION = 1000  # 倍率
TRIALS = 100  # 試行回数

pie_list = [ft_pi(MAGNIFICATION * i) for i in range(1,TRIALS + 1)]
x_list = [MAGNIFICATION * i for i in range(1, TRIALS + 1)]
print(pie_list[-1])
plt.plot(x_list, pie_list, label="my_pie")

y_pi = [math.pi for i in range(len(x_list))]
plt.plot(x_list, y_pi, label="PIE")

plt.xlabel("Number of plots")
plt.legend()
plt.show()

結果:
3.14696