np.random.choice(a, size, replace=False) は大きなサイズで遅い
きっかけは友人が開発している強化学習ライブラリの tf2rl に建てられたこちらの issue
TL; DR
重複なしの一様サンプリングを実施するにあたって、インデックス取得に np.random.choice(a, size, replace=False) を用いていたが、条件によっては非常に遅いということを知った話です。
(自ブログに書いた英語記事の日本語焼き直し)
重複なしサンプリングとその実装
np.random.choice は、公式ドキュメントに書いてあるように replace=False で重複を禁止した場合、np.random.permutation(np.arange(a))[:size] と等価になります。
実際に choice の実装を覗いてみると、前処理をいくつか行った後に permutation を呼んでいることが確認できます。
permutation はFisher-Yates shuffleで実装されており、乱数を a 個 (サンプリング対象の元データの個数) 生成しています。
一方、Pythonの標準ライブラリには、 random.sample(population, k) があり、random.sample(range(a), size)とすると (list型ですが) 上記のアルゴリズムと同じ結果を得られます。(公式ドキュメント)
CPython の実装では、 size 個 (サンプルする個数) の乱数を生成しています。
つまり、 a >> size の領域では numpy.random.choice を利用するよりも random.sample を利用する方が速いことが期待されます。この issue の事例では、a=1e6 (100万)、size=100 のためこの条件に該当します。 (強化学習に限らず機械学習では、巨大なデータセットから2桁程度のミニバッチを抽出するユースケースはしばしばありえると思っています。)
実験
実際に、サンプルされる範囲とサンプルする数をそれぞれ変えながら実験をしてみました。
(この記事を書くよりも前に実施した実験のため、変数名の使い方が異なっています。a -> d、size -> s)
前の章で説明した numpy.random.choice、numpy.random.permutation、random.sample に加え、サンプルされる範囲がサンプル個数で割り切れるときにのみ(簡単に)利用可能な層化抽出法 (Stratified sampling) を加えています。
実験コード
ベンチマークには perfplot を利用しています。乱数が絡んでいるので、出力結果の等値比較は無効化しています。内部的には timeit を活用しているとの記載があるので、繰り返し回数は実経過時間に応じて流動的です。 (誤差を評価するような厳密な実験をする上ではちょっと気になりますが、簡易的にはこれで十分だと思っています。)
import random
import numpy as np
import perfplot
perfplot.show(setup=lambda n: n,
kernels=[lambda d: np.random.choice(d, 100, replace=False),
lambda d: np.random.permutation(np.arange(d))[:100],
lambda d: np.arange(0, d, d//100) + np.random.randint(0, d//100, size=100),
lambda d: random.sample(range(d), 100)],
labels=["np.random.choice(d, 100, replace=False)", "np.random.permutation(np.arange(d))[:100]","np.arange(0, d, d//100) + np.random.randint(0, d//100, size=100)", "random.sample(range(d), 100)"],
n_range=[10 ** k for k in range(2, 7)],
equality_check=None,
xlabel="d: data size")
perfplot.show(setup=lambda n: n,
kernels=[lambda s: np.random.choice(int(1e6), s, replace=False),
lambda s: np.random.permutation(np.arange(int(1e6)))[:s],
lambda s: np.arange(0, int(1e6), int(1e6)//s) + np.random.randint(0, int(1e6)//s, size=s),
lambda s: random.sample(range(int(1e6)), s)],
labels=["np.random.choice(1e6, s, replace=False)", "np.random.permutation(np.arange(1e6))[:s]","np.arange(0, 1e6, 1e6//s) + np.random.randint(0, 1e6//s, size=s)", "random.sample(range(1e6), s)"],
n_range=[10 ** k for k in range(2, 6)],
equality_check=None,
xlabel="s: sample size")
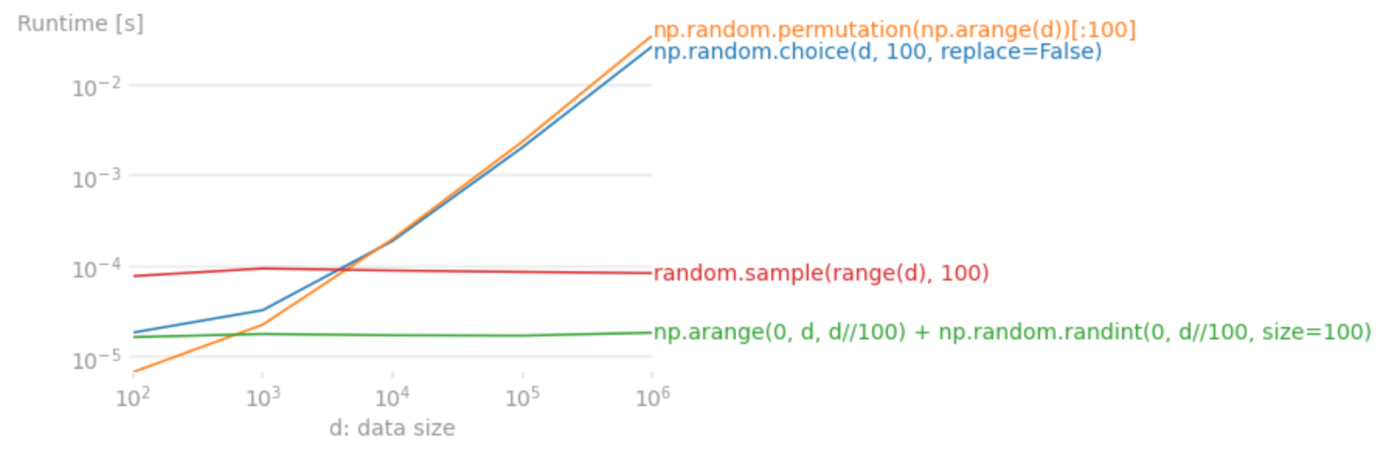
図1: サンプルする個数を100個に固定して、サンプルされる範囲を変えた場合の平均実行時間
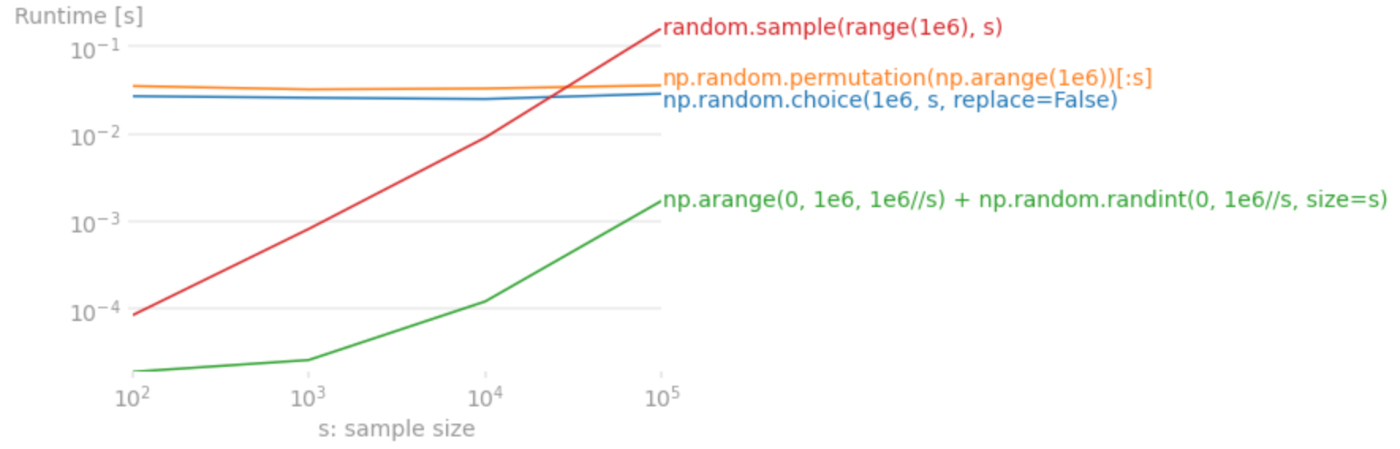
図2: サンプルされる範囲を1e6に固定して、サンプルする個数を変えた場合の平均実行時間
図1、図2の結果を見ると予想通り、numpy.random.choice と numpy.random.permutation はサンプルする範囲の数でスケールし、 random.sample (と層化抽出法) はサンプルする個数でスケールしています。
また、いずれのケースも層化抽出法が最速を叩き出しています。割り切れないときにあまりの部分をどうするのかが難しいところですが、割り切れるケースではこちらの採用も十分にありえると思います。
結論
遅いと言われた issue の解析をする中で、重複なし一様抽出の手法を調査・比較実験しました。
Numpyがいつも速いと思い込んでいましたが、条件によってはNumpyを使わないほうが速いことが実験的にも確かめられました。またベンチマークを実験することの重要性を改めて再認識しました。
おまけ
ここでは、np.random 直下のフリー関数を利用して書きましたが、現在の NumPy で推奨されているのは np.random.Generator オブジェクトを構築してそのメンバー関数を利用する方法です。
import numpy as np
rng = np.random.default_rng()
rng.choice(10, 5, replace=False)
グローバルオブジェクトの乱数状態ではなく、独立したオブジェクトに閉じ込めた乱数状態を利用することで複数スレッド・プロセスで同時に実行できるようになります。
追記 (2021/9/5)
レガシーAPI扱いのフリー関数 (np.random.choice) と異なり、推奨のnp.random.Generator.choice の実装はpermutation相当ではなく、ヒューリスティックな分岐が含まれていました。
そのため、「おまけ章」に記載している方法を使っていればそんなに性能上の問題にならないのじゃないかと思います。
Discussion