【強化学習】Large Batch Experience Replay (LaBER)
この記事は、強化学習 Advent Calendar 2021の12/3の記事です。
0. はじめに
強化学習のExperience Replayに興味がありZennで論文調査などの記事を書いたり、Replay Bufferライブラリ cpprb を開発したりしています。
今回、面白そうな論文があったので、その紹介と実装してみましたの記事です。
(cpprbのサイトのページの日本語焼き直しです。)
1. [論文紹介] Large Batch Experience Replay (LaBER)
T. Lahire et al., "Large Batch Experience Replay", CoRR (2021) (arXiv, code)
1.1 前提
強化学習(のoff-policyな手法)では、遷移 (一般には
2016年にT. Schaul等[1]は、この『ランダム』な取り出しを、完全な一様分布ではなく、Q学習で最小化するターゲットであるTD誤差に応じて選ぶ Prioritized Experience Replay (PER) を提案し、学習を速くできることを実験的に示しました。
PERは経験的にはうまく働くものも理論的にはなぜ良いのかは完全には明らかにはされてきませんでした。
1.2 提案手法
そこで著者らは、2017年のL. Wang等のSGDの収束速度の研究[2]に基づき、Replay Buffer上のデータを学習させる際の収束速度を最適化するサンプリング確率が
また、著者らはPERの実装上の課題として、一旦サンプルした遷移の重要度(=TD誤差)のみを更新するため、常に重要度が古いことも挙げています。
上記の2つの点を念頭に著者らは、重要度に厳密な値を利用する「Gradient Experience Replay (GER)」と、重要度は近似を用いるが最新の値を常に利用する「Large Batch Experience Replay (LaBER)」を提案し比較しました。
手法の関係性は以下の表のようになります。厳密な重要度計算は計算コストが高いので、最新の値を利用するのは現実的ではないと著者らは位置づけています。
| 重要度 | 厳密 | 近似 |
|---|---|---|
| 古い | GER | PER |
| 最新 | (非現実的) | LaBER |
では、近似であればサンプルの度に、Replay Buffer内の
そこで、LaBERでは、一旦少し大きめ(バッチサイズの
LaBERで利用する重要度の「近似」は、surrogate priority (代替重要度?) と呼んでいる
最適な分布に基づいてReplay Bufferからバッチ遷移を抽出する場合の期待値を算出して、surrogate priorityを代入すると以下のようになります。(
本来Replay Buffer全体で計算すべきの
LaBER-mean
LaBER-lazy
単純に無視する
LaBER-max
(PERで安定化のために正規化しているのを倣い)バッチの重みが最小になるように最大の値で正規化する
1.3 実験
著者らは、Atariのゲームを用いて包括的に実験を行い提案手法の検証をしました。
- surrogate priorityは近似を用いない本当の確率分布と同様の精度を達成できるのか?
- LaBERの精度はDQNを上回るのか?
-
m m - LaBERの正規化はどれを選べばよいのか?
- LaBERは設計思想どおり精度を挙げつつ、分散を抑えられるのか?
- LaBERで採用している重要度の最新化が鍵となっているのか?
以下に実験結果の一例を引用しますが、これらの結果を受け「surrogate priorityは十分によく近似している」「LaBERはDQNより精度が良く計算速度も速い」「
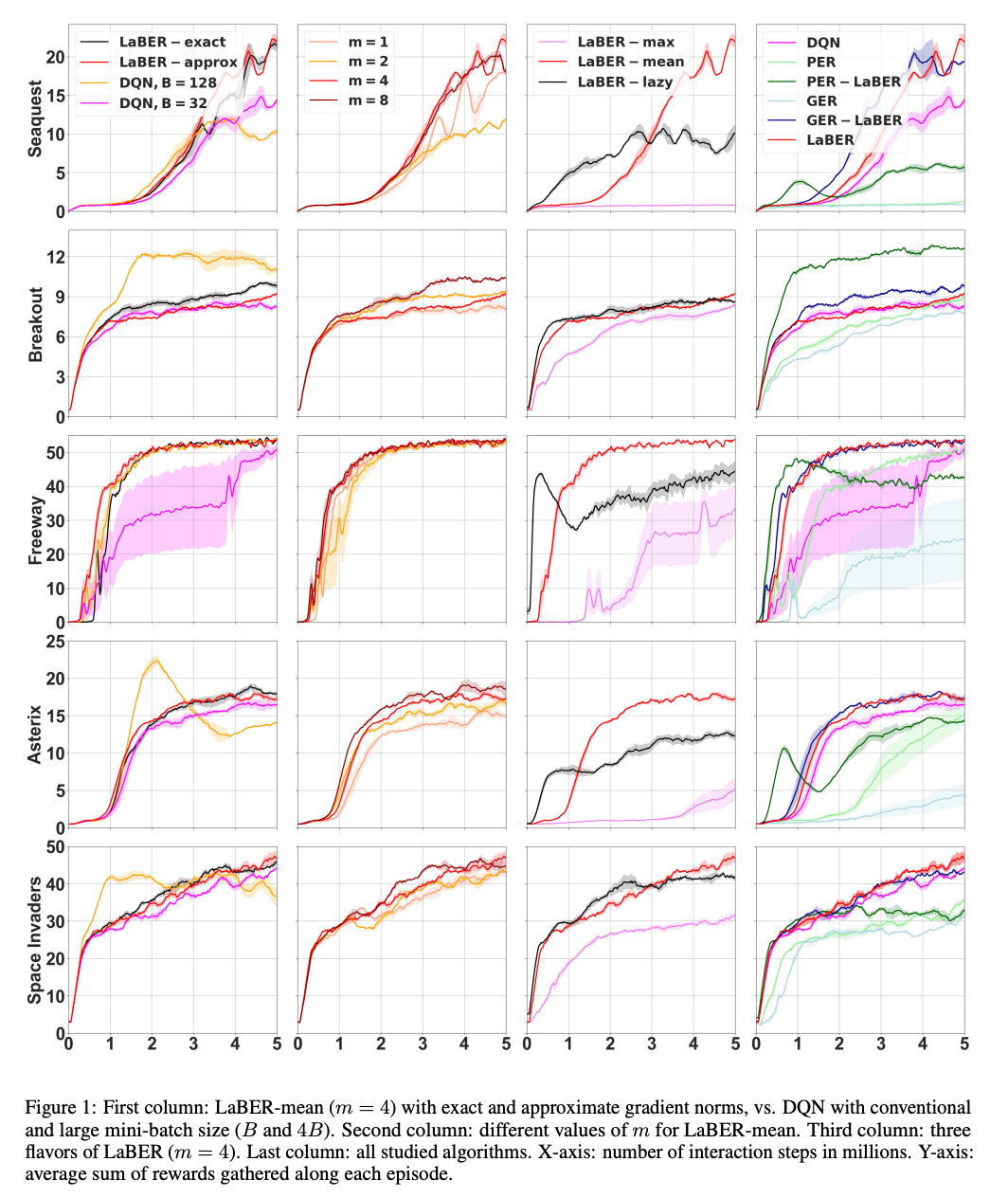
Atariのゲームにおける手法比較結果。最右列のPER-LaBER/GER-LaBERはPER/GERで
2. cpprbでの実装と利用方法
cpprbでは、LaBERはReplay Bufferそのものではなく、ReplayBufferクラスと一緒に使う補助的なクラスとして実装しました。
3つの手法がLaBERmean、LaBERlazy、LaBERmaxのクラスになっています。
ReplayBufferから取り出した
import cpprb
# LaBER-mean 用のクラス作成
laber = cpprb.LaBERmean(batch_size = 32, m = 4)
# Replay Buffer の作成などいつもの強化学習
rb = cpprb.ReplayBuffer(1e6, { ... })
...
# Replay Buffer からは、m倍のバッチサイズをまず取り出す。
sample = rb.sample(32 * 4)
# 取り出した遷移に対するsurrogate priorityを計算する
TD = ...
# surrogate priority に基づいてサブサンプリングし、インデックスと重みを得る。
index_weight = laber(priorities=TD)
index = index_weight["indexes"]
weight = index_weight["weights"]
# observation / action などの遷移の値自体を一緒に渡せば、
# 選ばれたインデックスに該当する値を一緒に返してくれるので、お好みで使い分けることができる
transitions = laber(priorities=TD, obs=sample["obs"], act=sample["act"])
index = transitions["indexes"]
weight = transitions["weights"]
obs = transitions["obs"]
act = transitions["act"]
3. サンプルコード
# Example for Large Batch Experience Replay (LaBER)
# Ref: https://arxiv.org/abs/2110.01528
import os
import datetime
import numpy as np
import gym
import tensorflow as tf
from tensorflow.keras.models import Sequential, clone_model
from tensorflow.keras.layers import Dense
from tensorflow.keras.optimizers import Adam
from tensorflow.summary import create_file_writer
from cpprb import ReplayBuffer, LaBERmean
gamma = 0.99
batch_size = 64
N_iteration = int(1e+6)
target_update_freq = 10000
eval_freq = 1000
egreedy = 1.0
decay_egreedy = lambda e: max(e*0.99, 0.1)
# Use 4 times larger batch for initial uniform sampling
# Use LaBER-mean, which is the best variant
m = 4
LaBER = LaBERmean(batch_size, m)
# Log
dir_name = datetime.datetime.now().strftime("%Y%m%d-%H%M%S")
logdir = os.path.join("logs", dir_name)
writer = create_file_writer(logdir + "/metrics")
writer.set_as_default()
# Env
env = gym.make('CartPole-v1')
eval_env = gym.make('CartPole-v1')
# For CartPole: input 4, output 2
model = Sequential([Dense(64,activation='relu',
input_shape=(env.observation_space.shape)),
Dense(env.action_space.n)])
target_model = clone_model(model)
# Loss Function
@tf.function
def Huber_loss(absTD):
return tf.where(absTD > 1.0, absTD, tf.math.square(absTD))
@tf.function
def MSE(absTD):
return tf.math.square(absTD)
loss_func = Huber_loss
optimizer = Adam()
buffer_size = 1e+6
env_dict = {"obs":{"shape": env.observation_space.shape},
"act":{"shape": 1,"dtype": np.ubyte},
"rew": {},
"next_obs": {"shape": env.observation_space.shape},
"done": {}}
# Nstep
nstep = 3
# nstep = False
if nstep:
Nstep = {"size": nstep, "rew": "rew", "next": "next_obs"}
discount = tf.constant(gamma ** nstep)
else:
Nstep = None
discount = tf.constant(gamma)
rb = ReplayBuffer(buffer_size,env_dict,Nstep=Nstep)
@tf.function
def Q_func(model,obs,act,act_shape):
return tf.reduce_sum(model(obs) * tf.one_hot(act,depth=act_shape), axis=1)
@tf.function
def DQN_target_func(model,target,next_obs,rew,done,gamma,act_shape):
return gamma*tf.reduce_max(target(next_obs),axis=1)*(1.0-done) + rew
@tf.function
def Double_DQN_target_func(model,target,next_obs,rew,done,gamma,act_shape):
"""
Double DQN: https://arxiv.org/abs/1509.06461
"""
act = tf.math.argmax(model(next_obs),axis=1)
return gamma*tf.reduce_sum(target(next_obs)*tf.one_hot(act,depth=act_shape), axis=1)*(1.0-done) + rew
target_func = Double_DQN_target_func
def evaluate(model,env):
obs = env.reset()
total_rew = 0
while True:
Q = tf.squeeze(model(obs.reshape(1,-1)))
act = np.argmax(Q)
obs, rew, done, _ = env.step(act)
total_rew += rew
if done:
return total_rew
# Start Experiment
observation = env.reset()
# Warming up
for n_step in range(100):
action = env.action_space.sample() # Random Action
next_observation, reward, done, info = env.step(action)
rb.add(obs=observation,
act=action,
rew=reward,
next_obs=next_observation,
done=done)
observation = next_observation
if done:
env.reset()
rb.on_episode_end()
n_episode = 0
observation = env.reset()
for n_step in range(N_iteration):
if np.random.rand() < egreedy:
action = env.action_space.sample()
else:
Q = tf.squeeze(model(observation.reshape(1,-1)))
action = np.argmax(Q)
egreedy = decay_egreedy(egreedy)
next_observation, reward, done, info = env.step(action)
rb.add(obs=observation,
act=action,
rew=reward,
next_obs=next_observation,
done=done)
observation = next_observation
# Uniform sampling
sample = rb.sample(batch_size * m)
with tf.GradientTape() as tape:
tape.watch(model.trainable_weights)
Q = Q_func(model,
tf.constant(sample["obs"]),
tf.constant(sample["act"].ravel()),
tf.constant(env.action_space.n))
target_Q = tf.stop_gradient(target_func(model,target_model,
tf.constant(sample['next_obs']),
tf.constant(sample["rew"].ravel()),
tf.constant(sample["done"].ravel()),
discount,
tf.constant(env.action_space.n)))
tf.summary.scalar("Target Q", data=tf.reduce_mean(target_Q), step=n_step)
absTD = tf.math.abs(target_Q - Q)
# Sub-sample according to surrogate priorities
# When loss is L2 or Huber, and no activation at the last layer,
# |TD| is surrogate priority.
sample = LaBER(priorities=absTD)
indexes = tf.constant(sample["indexes"])
weights = tf.constant(sample["weights"])
absTD = tf.gather(absTD, indexes)
assert absTD.shape == weights.shape, f"BUG: absTD.shape: {absTD.shae}, weights.shape {weights.shape}"
loss = tf.reduce_mean(loss_func(absTD)*weights)
grad = tape.gradient(loss, model.trainable_weights)
optimizer.apply_gradients(zip(grad, model.trainable_weights))
tf.summary.scalar("Loss vs training step", data=loss, step=n_step)
if done:
env.reset()
rb.on_episode_end()
n_episode += 1
if n_step % target_update_freq == 0:
target_model.set_weights(model.get_weights())
if n_step % eval_freq == eval_freq-1:
eval_rew = evaluate(model,eval_env)
tf.summary.scalar("episode reward vs training step",data=eval_rew,step=n_step)
4. おわりに
面白そうな手法LaBERの論文を読んで、自作のReplay Bufferライブラリcpprbに実装をし、簡単にですが紹介記事を書きました。
(本当は自分で実験して確認までしたかったのですが、記事の下書きが1ヶ月以上そのままでいつまでも完成しそうになかったので、Advent Calenderを機に、ここまででの公開としました。)
興味を持ってくれた人がいれば、cpprbを使ってもらえると私が喜びます。
Discussion