量子回路学習(QCL)の回路実装を読み解く

1. はじめに

量子回路学習(QCL: Quantum Circuit Learning)は、K. Mitarai等によって提案^[1]された量子機械学習の手法で、以下のようにパラメータ $\theta$、入力データ $x$ に基づくユニタリーゲートを適用した量子状態 $|\psi(\theta, x)\rangle$ を観測して得られた値を（古典）機械学習の回帰や分類に用いる手法です。

$$|\psi(\theta, x)\rangle = \rm{U}(\theta)\rm{U}(x)| 0\rangle ^{\otimes N}$$

$\rm{U}(x)$ はユニタリーな入力ゲート、$\rm{U}(\theta)$ はパラメータを持つユニタリーなゲートと記載されており、その選び方には自由度があるようです。
原論文ではこれ以上の名称をつけていませんが、指し示しづらいのでこの記事では後者 $\rm{U}(\theta)$ を変分ゲートと呼ぶことにします。

この記事では既存の実装例を読み解いてみようと思います。

2. 入力ゲート $\rm{U}(x)$

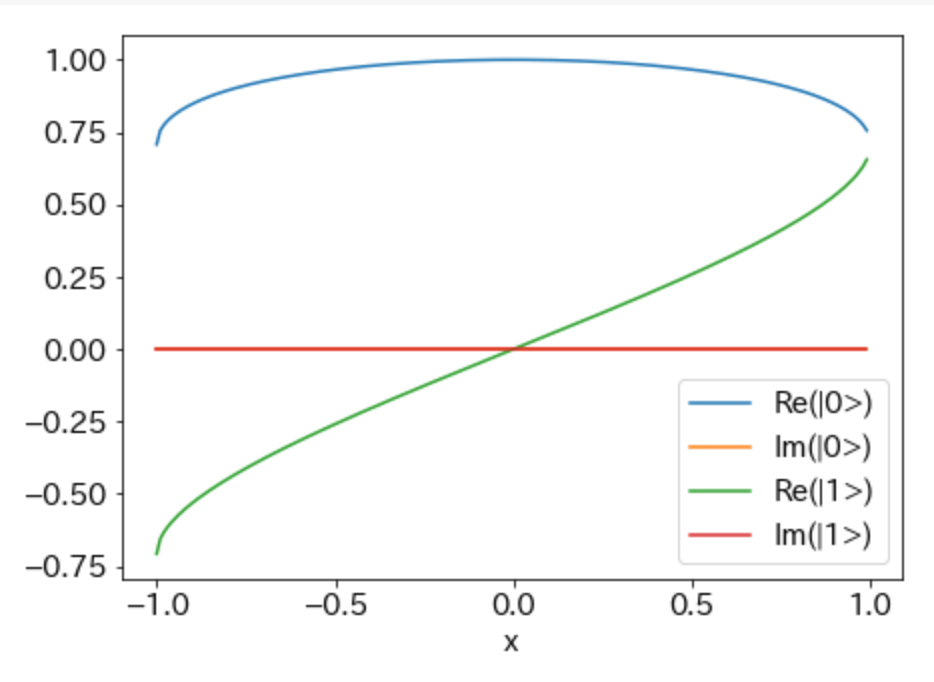
2.1 入力ゲート例①: $\rm{R_Y}(\sin^{-1}x)$

原論文^[1:1]のアルゴリズム説明で例示されている入力ゲートです。
(1次元の) $x$ を $N$ qubitsの量子回路に適用すると以下の様になると説明されています。

$$\rho _{\text{in}}(x) = \frac{1}{2^N}\bigotimes _{i=1}^N \left [ I + xX_i + \sqrt{1-x^2} Z_i \right ]$$

後続の回路で複数のqubitをもつれ（エンタングル）させることで、$1$, $x$, $\sqrt{1-x^2}$ から $N$ 個を掛け合わせた最高$N$次の非線形の項が出てきます。

私も最初勘違いしていたんですが、$N$次元のデータを$N$ qubitにエンコードするのではなく、1次元のデータを$N$ qubitにエンコードすることで、高次の影響を出すようです。
そのため $K$次元のデータで$k$番目のデータを$N_k$次までそれぞれ加味するとなると $\sum _{k=1}^K N_k$ qubit必要になります。

せっかくなので、開発中の自作ライブラリ diffqc を使って、$x \in [-1,1]$ で 1qubit の場合に入力ゲート適用後の確率振幅がどう変わるのかをシミュレーションしてみました。

実装

準備

import jax
import jax.numpy as jnp

import diffqc
from diffqc import dense as op

import matplotlib.pyplot as plt
import japanize_matplotlib
plt.rc("font", size=15)

入力ゲート①

@jax.vmap
def input_gate(x):
    c = op.zeros(1, jnp.complex64)
    c = op.RY(c, (0,), jnp.arcsin(x))
    return op.to_state(c)

# [-1, 1]
x = (jnp.arange(200, dtype=jnp.float32) / 100) - 1

rho = input_gate(x)

plt.figure(figsize=(7,5))
plt.plot(x, jnp.real(rho.at[:,0].get()), label="Re(|0>)")
plt.plot(x, jnp.imag(rho.at[:,0].get()), label="Im(|0>)")
plt.plot(x, jnp.real(rho.at[:,1].get()), label="Re(|1>)")
plt.plot(x, jnp.imag(rho.at[:,1].get()), label="Im(|1>)")
plt.xlabel("x")
plt.legend()
plt.show()

$X$ と $Z$ しか出てきていないので、実数部しか出てきていないですね。

2.2 入力ゲート例②: $\rm{R_Z}(\cos^{-1}x^2)\rm{R_Y}(\sin^{-1}x)$

同じく原論文^[1:2]の実験部分で（突然）出てくる入力ゲートです。

This unitary creates a state similar to Eq. (1)

とさらっと流されていましたが、こちらもシミュレーションで確認してみました。

実装

(準備部分は上と同じ)

入力ゲート②

@jax.vmap
def input_gate2(x):
    c = op.zeros(1, jnp.complex64)
    c = op.RY(c, (0,), jnp.arcsin(x))
    c = op.RZ(c, (0,), jnp.arccos(x**2))
    return op.to_state(c)

# [-1, 1]
x2 = (jnp.arange(200, dtype=jnp.float32) / 100) - 1

rho2 = input_gate2(x2)

plt.figure(figsize=(7,5))
plt.plot(x2, jnp.real(rho2.at[:,0].get()), label="Re(|0>)")
plt.plot(x2, jnp.imag(rho2.at[:,0].get()), label="Im(|0>)")
plt.plot(x2, jnp.real(rho2.at[:,1].get()), label="Re(|1>)")
plt.plot(x2, jnp.imag(rho2.at[:,1].get()), label="Im(|1>)")
plt.xlabel("x")
plt.legend()
plt.show()

原論文では similar と表現されていますが、確率振幅のグラフは少し複雑な動きをしているように見えます。
ちゃんと式展開していないですが、$1$, $x^2$, $\sqrt{1-x^4}$から$N$個、$1$, $x$, $\sqrt{1-x^2}$から$N$個を選んで掛け合わせる項が出てきそうですね。

書かれていないので推測でしかありませんが、qubit数を増やさずにより高次の影響を取り入れるために回転ゲートを増やしたのではないでしょうか。
更に高次の効果を取り入れたければ、$R_X(\sin^{-1}x^3)$ を追加するとかでしょうか。
ただ、ブロッホ球上の正規直交基底（独立な回転軸）は、$\lbrace X, Y, Z \rbrace$ の3種だと思うので、この方式ではそれ以上独立な成分を加えることはできなさそうですね。

2.3 入力ゲート例③: $U_{\Phi(x)}H^{\otimes N}U_{\Phi(x)}H^{\otimes N}$

V. Havlicek等の実機実装論文^[2]で提案されていた入力ゲートで、この論文では "Quantum feature map" と表現されていました。

$U_{\Phi(x)}$ の部分は以下のように $Z$ ゲートの組み合わせで表現されるゲートです。

$$U_{\Phi(x)} = \exp \left (i \sum _{S \subseteq [N]}\phi _S(x)\prod _{i \in S}Z_i \right )$$

$S$ はqubitの部分集合ですが、全ての qubit の組み合わせを考える必要はないらしく、論文中では例えば $|S|\leq 2$ だけを考えています。

$$U_{\Phi} = \exp \left \lbrace i \left ( x_1 Z_1 + x_2 Z_2 + (\pi - x_1)(\pi - x_2)Z_1Z_2 \right ) \right \rbrace$$

この入力ゲートは前節までに見てきた入力ゲートと異なり、この時点で既に複数qubit間のもつれが存在しています。

こちらは、2次元データを 2qubit にエンコードしているようです。

3. 変分ゲート $\rm{U}(\theta)$

3.1 変分ゲート例①: $[\exp (-iHT) \prod _{l} \prod _{i}\rm{U}(\theta _i^{(l)})] \times D\text{回}$

原論文^[1:3]の実験のセクションで利用された変分ゲートです。

上の式だとちょっとイメージ湧きにくいので、原論文の図を引用します。

原論文^[1:4]より引用

$H$ は横イジング模型のハミルトニアンで、以下のように表されます。

$$H = \sum _{j=1}^N a_j X_j + \sum _{j=1}^N \sum _{k=1}^{j-1} J_{jk}Z_jZ_k$$

原論文の実験では、係数 $a_j$ と $J_{jk}$ はそれぞれ、$[-1,1]$ の一様分布から生成して利用しています。

指数関数の上にハミルトニアンが乗っていると少しぎょっとしますが、物理的にはハミルトニアンに基づく時間発展演算子であり、量子コンピューターでは実行しやすいと原論文では言及しています。

シミュレーションにおいてはトロッター分解を用いて計算できます。

トロッター分解の実装例

変分ゲート自体は、乱数パラメータや複数のqubit等シミュレーションを可視化しづらいので、代わりにQuantum Native Dojoで紹介されている例を diffqc で実装してみます。

$$H = \sum_i^{N} Z_{i}Z_{i+1} + h \sum _i^N X_i$$

Isingシミュレーション

def trotter():
    nqubits = 6
    t = 3.0 # 時間
    M = 100 # 分割数
    delta = t / M
    h = 3.0

    c = op.zeros(nqubits, jnp.complex64)

    def step(ci, _):
        for i in range(nqubits):
            ci = op.RZZ(ci, (i, (i+1) % nqubits), 2*delta)
            ci = op.RX(ci, (i,), 2*h*delta)
        return ci, jnp.mean(jnp.asarray(tuple(op.expectZ(ci, (i,)) for i in range(nqubits))))

    x = jnp.arange(M) * delta
    _, m = jax.lax.scan(step, c, x)
    return x, m

plt.figure(figsize=(7, 5))
plt.plot(*trotter())
plt.show()

一般回転操作 $\rm{U}(\theta _j^{(l)})$ は以下のように3つの回転操作に分解して、それぞれの回転角パラメータを $[0,2\pi]$ の一様分布から生成して学習しています。

$$\rm{U}(\theta _j^{(l)}) = R_j^X(\theta ^{(l)}_{j1})R_j^Y(\theta ^{(l)}_{j2})R_j^X(\theta ^{(l)}_{j3})$$

3.2 変分ゲート例②: $\rm{U}_{\text{loc}}^{(D)}(\theta _D) \rm{U}_{\text{ent}} \dots \rm{U}_{\text{loc}}^{(2)}(\theta _2) \rm{U}_{\text{ent}}\rm{U}_{\text{loc}}^{(1)}(\theta _1)$

実装論文^[2:1]で利用された変分ゲートです。

$\rm{U}_{\text{ent}}$は $\rm{U}_{\text{ent}} = \prod _{(i,j) \in \mathcal{E}} CZ(i,j)$ なるコントロールゲートであり、チップ上の全結合$\mathcal{E}$に適用しており、$\rm{U}_{\text{loc}}$ は学習パラメータを持つ SU(2) 回転です。

この実装論文では入力ゲートで複雑なゲートを用いていたからなのか、変分ゲートは少し簡単なものになっているようですね。

複数層繰り返している変分ゲートの方を単純にする方が、実装上メリットがあるとかあるのでしょうか？
表現力の観点でも差があるのかもしれませんが、そこまでは読み解けませんでした。
誰か詳しい方がいれば教えていただけると嬉しいです。

4. まとめ

量子回路学習の論文で利用されているゲートの実装を読み解いて、一部の回路を拙作の diffqc でシミュレーションしてみました。
https://github.com/ymd-h/diffqc

diffqc については以前記事を書いたので、興味を持ったらこちらも読んでもらえると嬉しいです。
https://zenn.dev/ymd_h/articles/ea7f714dddd5af

脚注

1. K. Mitarai et al., "Quantum Circuit Learning", Phys. Rev. A 98, 032309 (2018), (arXiv:1803.00745)

2. V. Havlicek et al., “Supervised learning with quantum-enhanced feature spaces”, Nature 567, 209–212 (2019), (arXiv:1804.11326)