Neural SDEを用いた金融時系列データ生成

こんちわ、連日レベルが高い投稿が続いてる仮想通貨botter Advent Calendar 2023の15日目の記事です。

自分は、取引所の仕組みに詳しかったり、有効な戦略や便利なツールの情報を提供もできないので、機械学習に寄った記事を書くことをご容赦ください。
今回は、AIを使った金融時系列データの生成に関する記事を書こうと思います。

目的

人工的に金融時系列データを作り、mlbotが改善するかの実験を行う。

金融時系列データの活用方法は２つあると思っています。

1. backtestの精度を上げる
2. mlbot用の学習データとして使う

複雑な金融の時系列データといえど、確率分布にしたがって生成されていて、現実はその分布から１回だけサンプリングされている状況です。その１本のサンプリングされたパスだけでbacktestを行うとどうしてもbacktestの制度が下がってしまいます。そこで確率微分方程式からデータを沢山サンプリングして評価に活かすということが考えられます。またmlbotでdeep learningを使う場合はデータが多いほうがいいので、そのためのデータセット拡張に使うという方法も考えられます。

余談ですが、2で作ったデータで1で評価するのは、過学習を招きそうな気がしています。データ生成とデータ評価ようの　生成モデルは分けたほうが過学習を防げるかもしれません。現在のように１パスだけで学習して、評価するよりはどちらにしろましかもしれませんが。

金融時系列の生成方法

金融時系列の生成には、 Neural Stochastic Differential Equation（NSDE）を使う。NSDEは不規則な時系列データの生成で高い性能を持っています。

NSDEは以下のモデルで定式化されています。

$$dY_t = \mu_{\theta}(t, Y_t)dt + \sigma_{\theta}(t, Y_t) \circ dW_t,\qquad X^{\theta}_t = A_{\theta}Y_t + b_{\theta}$$

$X_t$という時系列データが$Y_t$の中のノイズ$W_t$を通して生成されている。今回は、観測された金融時系列データ$X_t$とモデルが生成した$X^{\theta}_t$が一致するようにモデル内のパラメータ$\theta$をニューラルネットで学習することを目指します。

以下細かい定義とかが気になる人向け

ニューラル確率微分方程式（SDEs）は、$d_w$-次元ブラウニアン運動 $W : [0, T] \to \mathbb{R}^{d_w}$ と、標準正規分布に従う $d_a$-次元のノイズ $a \sim N(0, I_{d_a})$ を基に構築されます。ここで、$d_w$ と $d_a$ はノイズの大きさを記述するハイパーパラメータです。

ニューラルSDEは以下の形式のモデルです：

$$Y_0 = \xi_{\theta}(a),$$

$$dY_t = \mu_{\theta}(t, Y_t)dt + \sigma_{\theta}(t, Y_t) \circ dW_t,$$

$$X^{\theta}_t = A_{\theta}Y_t + b_{\theta}$$

ここで、$t \in [0, T]$ とし、$Y : [0, T] \to \mathbb{R}^{d_y}$ はストラトノビッチSDEの強解です。初期状態マップ $\xi_{\theta}: \mathbb{R}^{d_a} \to \mathbb{R}^{d_y}$、ドリフト項 $\mu_{\theta}: [0, T] \times \mathbb{R}^{d_y} \to \mathbb{R}^{d_y}$、拡散項 $\sigma_{\theta}: [0, T] \times \mathbb{R}^{d_y} \to \mathbb{R}^{d_y} \times \mathbb{R}^{d_w}$ は適切な規則性を持つニューラルネットワークで表されます。$A_{\theta} \in \mathbb{R}^{d_x \times d_y}$ と $b_{\theta} \in \mathbb{R}^{d_x}$ はそれぞれニューラルネットワークのパラメータです。$d_y \in \mathbb{N}$は隠れ状態のサイズを表すハイパーパラメータです。$\mu_{\theta}$ と $\sigma_{\theta}$ がリプシッツ連続であり、期待値 $E_a[\xi_{\theta}(a)^2] < \infty$ のとき、解 $Y$ は存在し一意です。

NSDEは確率微分方程式を推定するため、等間隔の時間でデータがなくても使えます。これはサーバーからデータが歯抜けになる場合や、取引所がメンテナンスをしていて部分的にデータが観測できないような状況にも自然に対応できることを意味します。また異なるスケールのデータを取り込むことも可能です。NSDEでは、真のパスと生成されたパスの距離をの測定にadversarialな手法をよく用いますが、mode collapseが起き最適化が難しいため、今回はシグネーチャースコアを用いた方法を使います。シグネーチャースコアはシグネーチャーカーネルを用いて、真のパスと生成されたパスの間の距離を定量化するもで、確率の測度を一意に定めることができるため、安定してNSDEを学習することができます。またノイズのモデル化にはブラウン運動を使いました。既存研究では非整数型ブラウン運動に拡張したものも提案されていますが、結果はあまり変わらないという結論だったので楽をしました。ちゃんとやるなら非整数型ブラウン運動を使うほうが良いと思います。

以下は論文のFigure1にあったシグネーチャースコアベース(左)とAdversarialベース(右)のNSDEの比較です。EURUSDとUSDJPYそれぞれの値動きを学習し、１０２４サンプル生成して、相関を比較していました。青が本当のデータの相関で、赤が生成されたデータが生み出した相関です。結果は、シグネーチャースコアベースだけが真の相関と同じ負の相関を捉えられています。

論文から引用

実験

setup

• BTCUSD closeの15分足
• scale 0.1 ← 非常に重要だった。(学習は比較的安定だが、scaleにはすごい依存するので注意)

学習は1 gpu(RTX2080Ti)で3時間くらいです。

生成結果

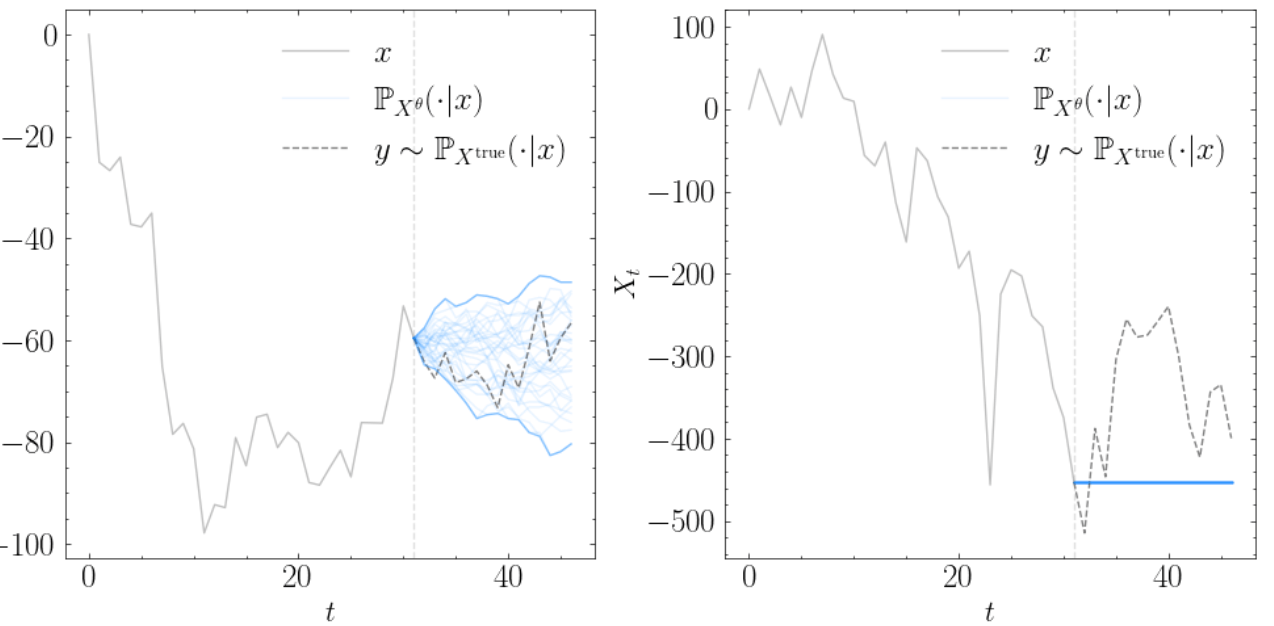
NSDEを学習し、条件付確率でサンプリングした結果の図を２つ紹介します。黒い線が実際のデータで最初のt=32までを使い条件付しています。t=32~48にある青い線が生成されたパスです。
論文の主張通り、平均回帰性、マルチンゲール、レバレッジ効果が確認できます(目視なのでお気持ちかもしれないですが)。

失敗例

以下の例のようにcondtionのpathのボラティリティが高い場合、予測が意味をなさない生成を行うことが多かったです。左がボラティリティが低い場合、右が高い場合です(縦軸の違いに注目)。このような場合、左はうまくいくのですが、右は意味のない予測になっています。
実用上はこういうものを除外するか、こういうものを出力しないように前処理を行う必要があるかもしれないです。
例えば、林・中川の論文ではcloseではなく対数リターンを標準化した時系列データ用いて学習し、生成ししたあとに変換をかけることでcloseのチャートに戻しているようでした。今回は、シグネーチャーカーネルの論文に従いパスの最初がかならず0になるような前処理を行いました。

ここでこの記事に目的を思い出してみると、
目的：人工的に金融時系列データを作り、mlbotが改善するかの実験を行う。← すいません間に合わなかったです😇

機会があれば、実験の続きをしてどこかで結果を公開したいと思います。。。

参考文献

• NSDEの論文
• 林・中川の論文