CPCV(Combinatorial Purged Cross-Validation)法
この記事は、Kaggle Advent Calendar[1]の2021/12/14の記事です。
目的
時系列データ(特にCVが不安定な場合)に対して安定したvalidationを行いたい。
背景
kaggleにおいてvalidationは重要である。validationとはモデルの性能を過学習をさけて測定する方法で、ハイパーパラメータを決めるためや、未知のデータに対する予測精度を正しく測るために用いられる。
しかし金融データのような予測対象の分散が大きい場合に安定してvalidationを行うことは難しい。そこでそういう場合でもより頑健にvalidationを行うことができるCPCV(Combinatorial Purged Cross-Validation)の紹介を行う。CPCVはkaggleの金融系コンペ[2][3]で議論に上がってるのをみかける。
この記事では具体的に説明するために1月~6月までの株価データがあったときの株価予測を題材にすすめる。
※わかりやすかったので図はここから引用させていただいた[4]
既存の方法
Walk forward(WF)
データを分割し、trainデータより未来のデータを使いvalidationをする

欠点:すべてのデータを検証に使えない(どうしても最初のデータは使えない)
Cross-validation(CV)
データを分割し、trainに使ったデータ以外でvalidationを行うことを繰り返す。
理論的には、竹内情報量基準と等価

欠点:バックテストの経路が1つしかない
CPCV(Combinatorial Purged Cross-Validation)
CVのvalidationに2ブロック以上を使う
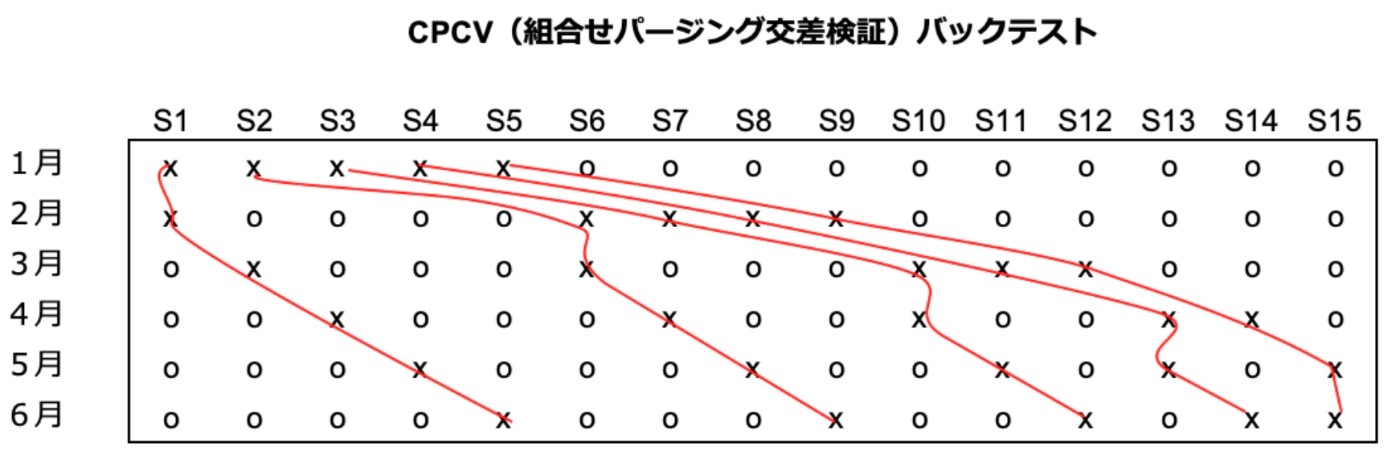
この例では
5通りのback test(行で見ると
利点:複数のバックテストの経路が存在する
CPCVを行うときのテクニックPurgingとEmbargo

Purging: tranとvalidationがoverlapしないように間を開けること
Embargo: validationから次のtrainの間を余分に開けること
分散が大きいデータでハイパーパラメータチューニングをすると過学習することを示す
測定するデータの分散が大きいことから投資戦略(モデル)のシャープレシオ[5]の分散が大きい場合高いシャープレシオを持つ戦略が見つかってしまうということを示す。
N個の学習済みモデルを考えるn番目のモデルの標本集団に対するシャープレシオが
Eはデータ方向の期待値
nはモデルの足
データの分散が大きいせいでn番目のモデルのデータ方向の分散は大きくなる
結果として良い投資戦略

分散が大きいデータでハイパーパラメータチューニングをすると過学習することを示す図[6]
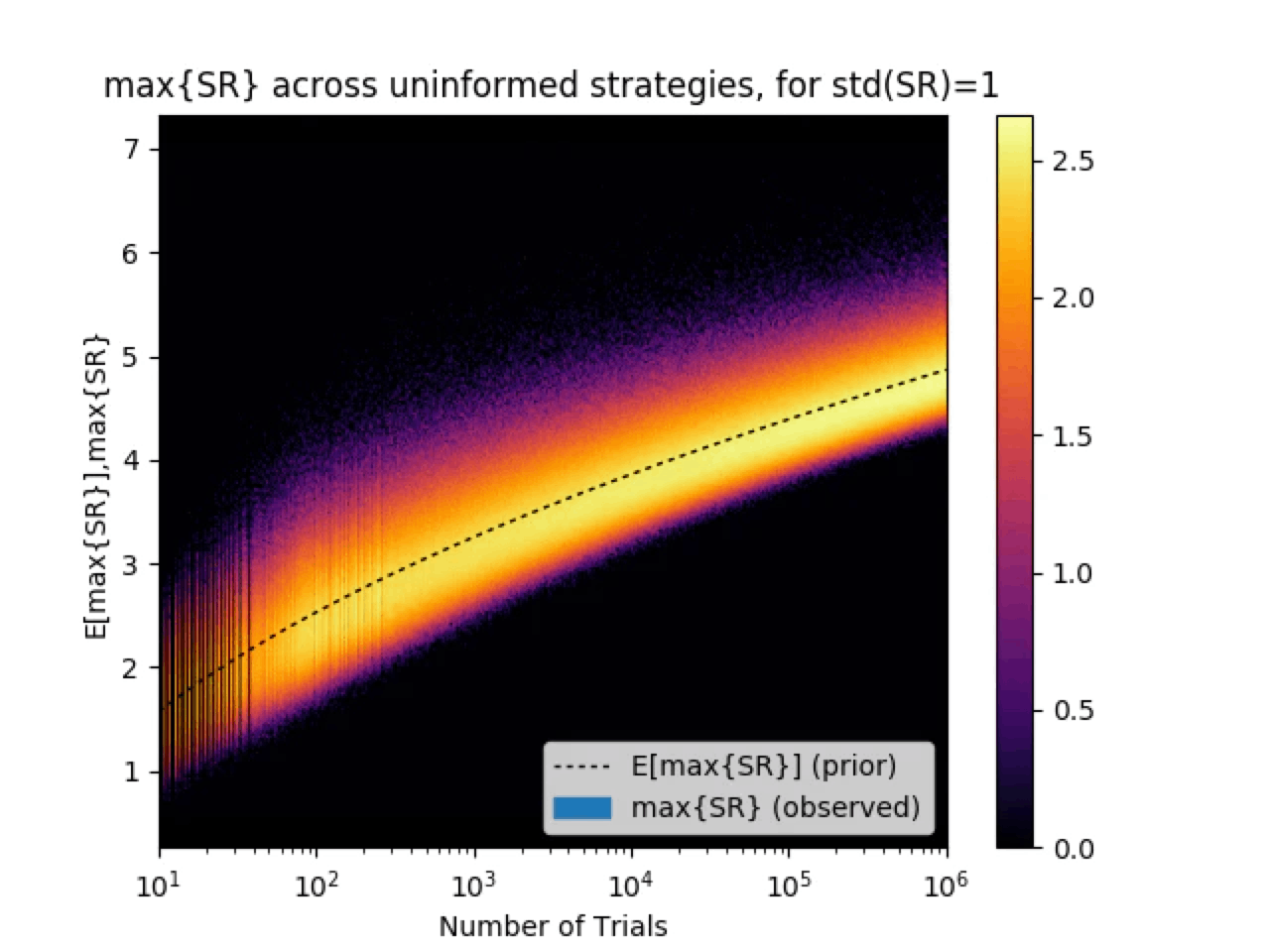
縦軸:back testのシャープレシオの最大値
横軸:投資戦略の数(作ったモデルの数)
色:オレンジほど起こりやすい
黒点線:最大シャープレシオの期待値
直感的にも用意する戦略を増やして、分散が大きいときに期待値の中でmaxとれば期待値は大きくなるのは当然
なぜWFとCVはだめでCPCVはオーバーフィットを緩和できるのか?
WFは使えるデータ数が少ないため、
CVはデータ数は大きいがback testのパスが1つなので
結論からいうとCPCVが
CPCVが\sigma\left[y_{n}\right]
CPCVではJ本のback testパスをつくれるのでパスの標本平と分散がとれる
標本平均
標本分散
と定義する
CPCVの標本平均の分散は
相関係数なので
なぜなら
つまり標本分散より標本平均の分散のほうが小さいことを意味する
経路間の相関が低くなると
となり
実際はJに上限はあるがかなり大きい値が取れる
実装
以下のvalidation法の比較を行う
- CV
- PurgedGroupTimeSeriesSplit
- CPCV
それぞれのイメージ
from sklearn.model_selection import KFold
cv = KFold(5)

from cv import PurgedGroupTimeSeriesSplit
cv = PurgedGroupTimeSeriesSplit(
n_splits=n_splits,
max_train_group_size=200,
group_gap=4*12,
max_test_group_size=150
)

from cv import CombPurgedKFoldCV
N=5
K=2
time_gap = 50
embargo_td = pd.Timedelta(100)
cv = CombPurgedKFoldCV(n_splits=N, n_test_splits=K, time_gap=time_gap, embargo_td=embargo_td)
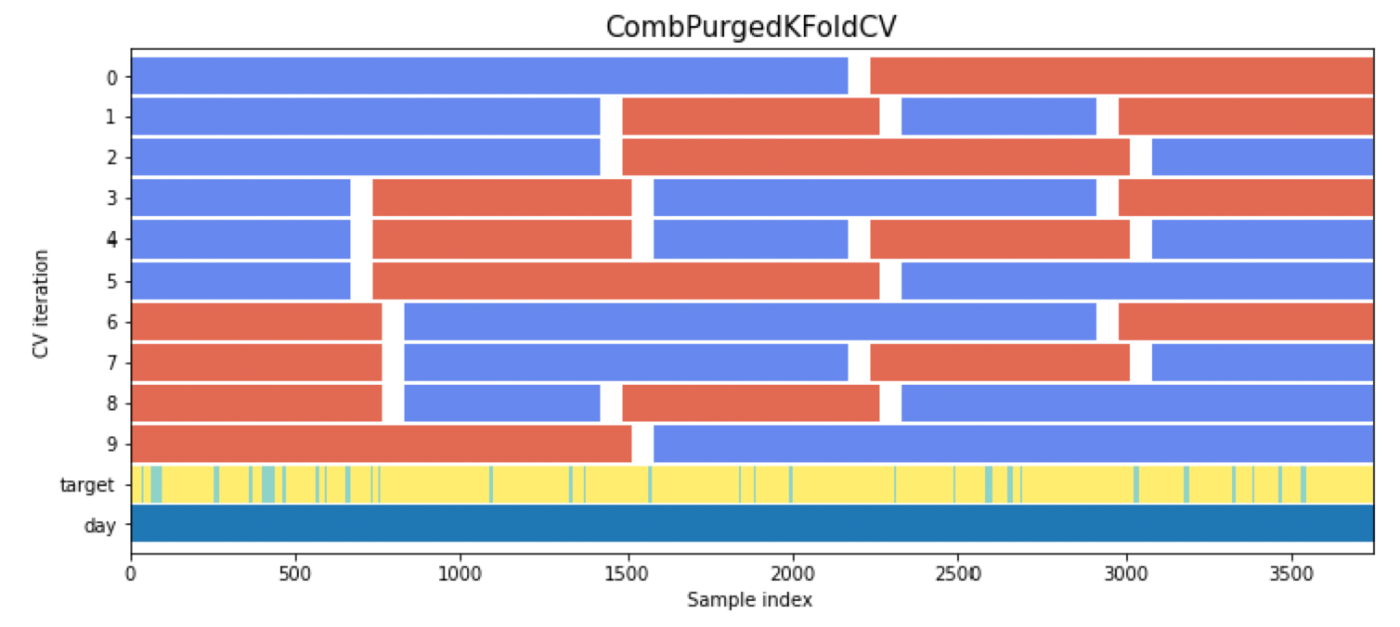
CPCVの実装 (これを改造[7])
class CombPurgedKFoldCV(BaseTimeSeriesCrossValidator):
"""
Purged and embargoed combinatorial cross-validation
As described in Advances in financial machine learning, Marcos Lopez de Prado, 2018.
The samples are decomposed into n_splits folds containing equal numbers of samples, without shuffling. In each cross
validation round, n_test_splits folds are used as the test set, while the other folds are used as the train set.
There are as many rounds as n_test_splits folds among the n_splits folds.
Each sample should be tagged with a prediction time pred_time and an evaluation time eval_time. The split is such
that the intervals [pred_times, eval_times] associated to samples in the train and test set do not overlap. (The
overlapping samples are dropped.) In addition, an "embargo" period is defined, giving the minimal time between an
evaluation time in the test set and a prediction time in the training set. This is to avoid, in the presence of
temporal correlation, a contamination of the test set by the train set.
Parameters
----------
n_splits : int, default=10
Number of folds. Must be at least 2.
n_test_splits : int, default=2
Number of folds used in the test set. Must be at least 1.
embargo_td : pd.Timedelta, default=0
Embargo period (see explanations above).
"""
def __init__(self, n_splits=10, n_test_splits=2, time_gap=0, embargo_td=0):
super().__init__(n_splits)
if not isinstance(n_test_splits, numbers.Integral):
raise ValueError(f"The number of test folds must be of Integral type. {n_test_splits} of type "
f"{type(n_test_splits)} was passed.")
n_test_splits = int(n_test_splits)
if n_test_splits <= 0 or n_test_splits > self.n_splits - 1:
raise ValueError(f"K-fold cross-validation requires at least one train/test split by setting "
f"n_test_splits between 1 and n_splits - 1, got n_test_splits = {n_test_splits}.")
self.n_test_splits = n_test_splits
if not isinstance(time_gap, int):
raise ValueError("time gap type is int")
self.time_gap = time_gap
if isinstance(embargo_td, int):
if embargo_td < 0:
raise ValueError(f"The embargo time should be positive, got embargo = {embargo_td}.")
if isinstance(embargo_td, pd.Timedelta):
if embargo_td < pd.Timedelta(0):
raise ValueError(f"The embargo time should be positive, got embargo = {embargo_td}.")
self.embargo_td = embargo_td
def split(self, X: pd.DataFrame, y: pd.Series = None,
pred_times: pd.Series = None, eval_times: pd.Series = None) -> Iterable[Tuple[np.ndarray, np.ndarray]]:
"""
Yield the indices of the train and test sets.
Although the samples are passed in the form of a pandas dataframe, the indices returned are position indices,
not labels.
Parameters
----------
X : pd.DataFrame, shape (n_samples, n_features), required
Samples. Only used to extract n_samples.
y : pd.Series, not used, inherited from _BaseKFold
pred_times : pd.Series, shape (n_samples,), required
Times at which predictions are made. pred_times.index has to coincide with X.index.
eval_times : pd.Series, shape (n_samples,), required
Times at which the response becomes available and the error can be computed. eval_times.index has to
coincide with X.index.
Returns
-------
train_indices: np.ndarray
A numpy array containing all the indices in the train set.
test_indices : np.ndarray
A numpy array containing all the indices in the test set.
"""
if pred_times is None:
pred_times = pd.Series(X.index).shift(self.time_gap).bfill()
pred_times.index = X.index
if eval_times is None:
eval_times = pd.Series(X.index).shift(-self.time_gap).ffill()
eval_times.index = X.index
super().split(X, y, pred_times, eval_times)
# Fold boundaries
fold_bounds = [(fold[0], fold[-1] + 1) for fold in np.array_split(self.indices, self.n_splits)]
# List of all combinations of n_test_splits folds selected to become test sets
selected_fold_bounds = list(itt.combinations(fold_bounds, self.n_test_splits))
# In order for the first round to have its whole test set at the end of the dataset
selected_fold_bounds.reverse()
for fold_bound_list in selected_fold_bounds:
# Computes the bounds of the test set, and the corresponding indices
test_fold_bounds, test_indices = self.compute_test_set(fold_bound_list)
# Computes the train set indices
train_indices = self.compute_train_set(test_fold_bounds, test_indices)
yield train_indices, test_indices
def compute_train_set(self, test_fold_bounds: List[Tuple[int, int]], test_indices: np.ndarray) -> np.ndarray:
"""
Compute the position indices of samples in the train set.
Parameters
----------
test_fold_bounds : List of tuples of position indices
Each tuple records the bounds of a block of indices in the test set.
test_indices : np.ndarray
A numpy array containing all the indices in the test set.
Returns
-------
train_indices: np.ndarray
A numpy array containing all the indices in the train set.
"""
# As a first approximation, the train set is the complement of the test set
train_indices = np.setdiff1d(self.indices, test_indices)
# But we now have to purge and embargo
for test_fold_start, test_fold_end in test_fold_bounds:
# Purge
train_indices = purge(self, train_indices, test_fold_start, test_fold_end)
# Embargo
train_indices = embargo(self, train_indices, test_indices, test_fold_end)
return train_indices
def compute_test_set(self, fold_bound_list: List[Tuple[int, int]]) -> Tuple[List[Tuple[int, int]], np.ndarray]:
"""
Compute the indices of the samples in the test set.
Parameters
----------
fold_bound_list: List of tuples of position indices
Each tuple records the bounds of the folds belonging to the test set.
Returns
-------
test_fold_bounds: List of tuples of position indices
Like fold_bound_list, but with the neighboring folds in the test set merged.
test_indices: np.ndarray
A numpy array containing the test indices.
"""
test_indices = np.empty(0)
test_fold_bounds = []
for fold_start, fold_end in fold_bound_list:
# Records the boundaries of the current test split
if not test_fold_bounds or fold_start != test_fold_bounds[-1][-1]:
test_fold_bounds.append((fold_start, fold_end))
# If the current test split is contiguous to the previous one, simply updates the endpoint
elif fold_start == test_fold_bounds[-1][-1]:
test_fold_bounds[-1] = (test_fold_bounds[-1][0], fold_end)
test_indices = np.union1d(test_indices, self.indices[fold_start:fold_end]).astype(int)
return test_fold_bounds, test_indices
def compute_fold_bounds(cv: BaseTimeSeriesCrossValidator, split_by_time: bool) -> List[int]:
"""
Compute a list containing the fold (left) boundaries.
Parameters
----------
cv: BaseTimeSeriesCrossValidator
Cross-validation object for which the bounds need to be computed.
split_by_time: bool
If False, the folds contain an (approximately) equal number of samples. If True, the folds span identical
time intervals.
"""
if split_by_time:
full_time_span = cv.pred_times.max() - cv.pred_times.min()
fold_time_span = full_time_span / cv.n_splits
fold_bounds_times = [cv.pred_times.iloc[0] + fold_time_span * n for n in range(cv.n_splits)]
return cv.pred_times.searchsorted(fold_bounds_times)
else:
return [fold[0] for fold in np.array_split(cv.indices, cv.n_splits)]
def embargo(cv: BaseTimeSeriesCrossValidator, train_indices: np.ndarray,
test_indices: np.ndarray, test_fold_end: int) -> np.ndarray:
"""
Apply the embargo procedure to part of the train set.
This amounts to dropping the train set samples whose prediction time occurs within self.embargo_dt of the test
set sample evaluation times. This method applies the embargo only to the part of the training set immediately
following the end of the test set determined by test_fold_end.
Parameters
----------
cv: Cross-validation class
Needs to have the attributes cv.pred_times, cv.eval_times, cv.embargo_dt and cv.indices.
train_indices: np.ndarray
A numpy array containing all the indices of the samples currently included in the train set.
test_indices : np.ndarray
A numpy array containing all the indices of the samples in the test set.
test_fold_end : int
Index corresponding to the end of a test set block.
Returns
-------
train_indices: np.ndarray
The same array, with the indices subject to embargo removed.
"""
if not hasattr(cv, 'embargo_td'):
raise ValueError("The passed cross-validation object should have a member cv.embargo_td defining the embargo"
"time.")
last_test_eval_time = cv.eval_times.iloc[cv.indices[:test_fold_end]].max()
min_train_index = len(cv.pred_times[cv.pred_times <= last_test_eval_time + cv.embargo_td])
if min_train_index < cv.indices.shape[0]:
allowed_indices = np.concatenate((cv.indices[:test_fold_end], cv.indices[min_train_index:]))
train_indices = np.intersect1d(train_indices, allowed_indices)
return train_indices
def purge(cv: BaseTimeSeriesCrossValidator, train_indices: np.ndarray,
test_fold_start: int, test_fold_end: int) -> np.ndarray:
"""
Purge part of the train set.
Given a left boundary index test_fold_start of the test set, this method removes from the train set all the
samples whose evaluation time is posterior to the prediction time of the first test sample after the boundary.
Parameters
----------
cv: Cross-validation class
Needs to have the attributes cv.pred_times, cv.eval_times and cv.indices.
train_indices: np.ndarray
A numpy array containing all the indices of the samples currently included in the train set.
test_fold_start : int
Index corresponding to the start of a test set block.
test_fold_end : int
Index corresponding to the end of the same test set block.
Returns
-------
train_indices: np.ndarray
A numpy array containing the train indices purged at test_fold_start.
"""
time_test_fold_start = cv.pred_times.iloc[test_fold_start]
# The train indices before the start of the test fold, purged.
train_indices_1 = np.intersect1d(train_indices, cv.indices[cv.eval_times < time_test_fold_start])
# The train indices after the end of the test fold.
train_indices_2 = np.intersect1d(train_indices, cv.indices[test_fold_end:])
return np.concatenate((train_indices_1, train_indices_2))
testとvalidationの比較を本来は載せるべきですが、時間がなかったです。
手元のデータでのvalidationスコアはcpcvがcvと比べて低め(高いほうがいい場合)にでてました。
Discussion