🔥
作って意地でも理解するフォントがレンダリングされるまで

2025/10/15に公開
いきなりですが、2つ質問です。今まさにあなたが読んでいる文字がどうやってレンダリングされているか説明できますか？私はできませんでした。それではあるモノの仕組みを理解するために最も効率の良い方法は何でしょうか？そう、自作することです！それではフォントのパーサーとレンダラーをゼロから作っていきましょう！

 目的小さなTrueTypeレンダラーを自作し、フォントがレンダリングされるまで流れを理解することが目的です。具体的には、Unicodeのフォントを読み込んで、任意の文字列をレンダリングしpngファイルとして書き出すまでを目標とします。実装はほぼプレーンなC++で、ベクトル演算用にglm、png書き出し用にstb_image_writeを使います。コード全体は以下から確認できます。

 TrueTypeとはTrueTypeとはAppleが1990年に開発したフォントのフォーマットです。その後Microsoftに無償で技術提供され、現在に至るまで標準的なフォントフォーマットの一つとして使われています。TrueTypeの仕様書はAppleの公式サイトから見ることができます。

https://developer.apple.com/fonts/TrueType-Reference-Manual/

 超ざっくりTrueTypeの仕組みTrueTypeはグリフにベクター画像を用いることにより、スケーラブルなレンダリングを実現するフォントフォーマットです。つまり、最小構成要素は点で、点を結んで線を作り、線をつなげて輪郭を作り、輪郭を塗りつぶせばグリフをレンダリングできるということです。

TrueTypeにおいて線は直線と曲線の二種類に分類され、曲線は二次ベジエ曲線を用いて表します。そして線をつなぐと輪郭(Contour)になります。グリフの輪郭と言われてもイメージがつきにくいかもしれませんが、たとえば以下の"B"は外側の輪郭が1つ、内側に2つ、合計3つの輪郭で構成されています。


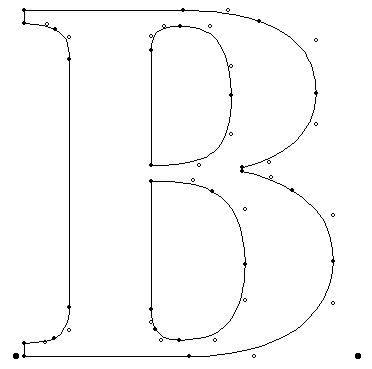
Digitizing Letterform Designs - TrueType Reference Manual - Apple Developerより引用
またグリフによっては、複数のグリフを組み合わせて表現できることもあります。これをコンパウンドグリフと呼びます。例えば、"Ü"は"U"を使ったコンパウンドグリフです。このようにして一つのグリフに必要な輪郭を全て得ることができたら、塗りつぶして完成です。

そしてTrueTypeのデータはテーブルで表されます。テーブルと言ってもバイト列に直接データが詰まっているのであくまで1次元的で、例えばcmapテーブルにアクセスするためにはファイルの先頭からXXXXバイト移動してアクセスするようなイメージです。


この図はあくまでイメージでテーブルの並びやバイト数は適当です
TrueTypeの"輪郭"が少し見えてきたでしょうか？するといくつかの疑問が頭に浮かんでくると思います。グリフのデータにはどうやってアクセスするのか？曲線はどうやってレンダリングするのか？塗りつぶしの方法は？などなど…ここではその感覚を実装に入る前に得られれば十分です。それでは実際にTrueTypeファイルのパースに入っていきましょう！

 TrueTypeパーサー　グリフデータの取得準備パーサー側の主なゴールはUnicodeからグリフデータを得ることです。ただし一筋縄ではいかず、たくさんのテーブルを見て回ってグリフのための情報を集めてくる必要があります。以下の図はグリフデータを得るまでにアクセスするテーブルのフローです。

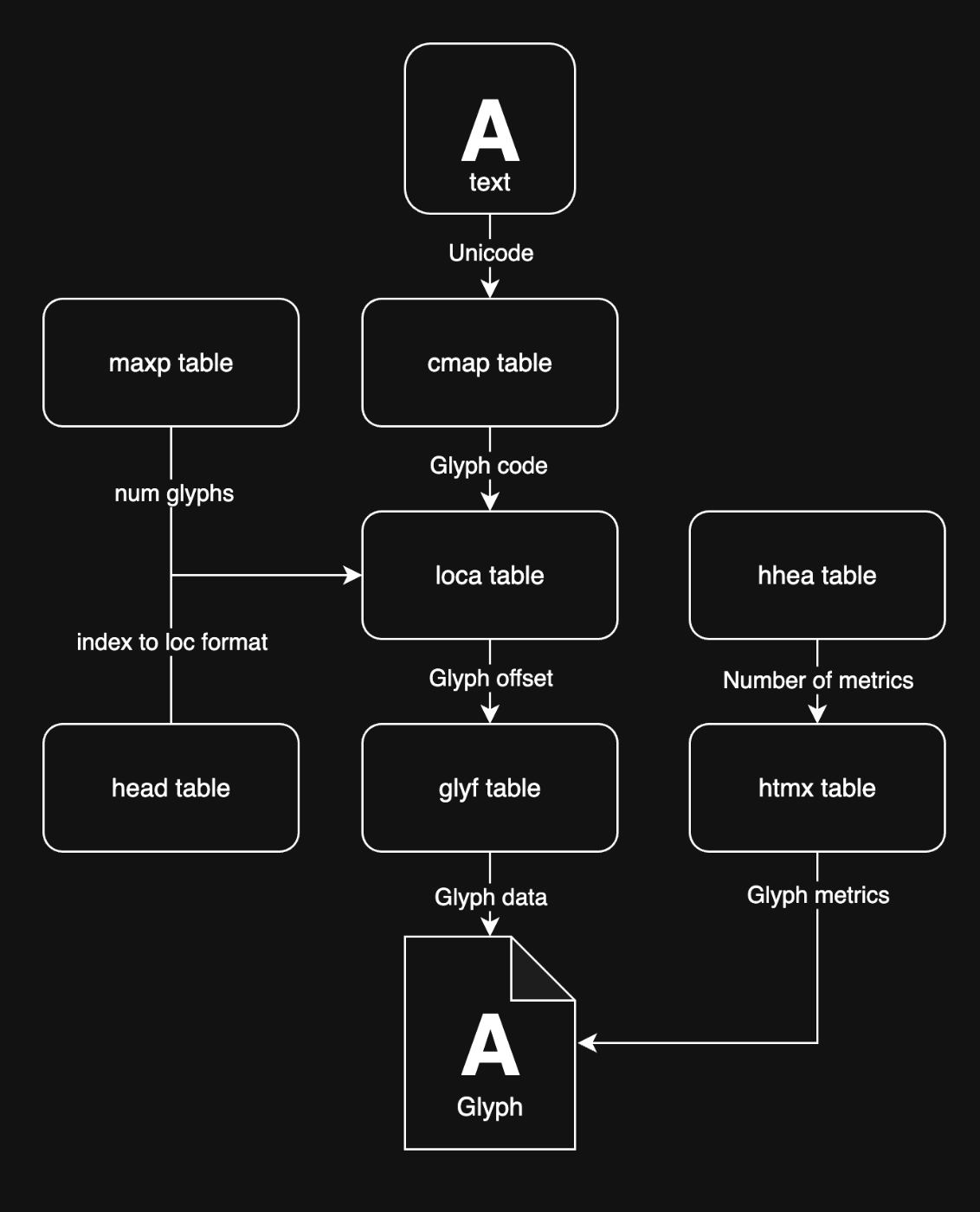
 ttfファイル読み込みまずはFontParserクラスを作って.ttfファイルを開き、データにアクセスできるようにします。基本的には特定のバイトオフセットにジャンプして何バイトずつか読み込む、の繰り返しなので、以下のようにナビゲーション用のメソッドを用意します。ここでの実装上の注意点としては、TrueTypeのデータはビッグエンディアンであることです。

ちなみに、TrueTypeにはuint, intなどの一般的な型以外に以下のような特別なデータ型が存在します。特にF2Dot14は精度が必要なグリフの変形に用いられる大事な型なので、合わせてメソッドを作ってしまいましょう。


型
説明


shortFrac
16-bit 符号付き小数

Fixed
16.16-bit 符号付き固定小数点数

FWord
16-bit 符号付き整数 (単位: FUnit)

uFWord
16-bit 符号なし整数 (単位: FUnit)

F2Dot14
16-bit 符号付き固定小数点数 上位2ビットが整数部、下位14ビットが小数部

longDateTime
64-bit 1904年1月1日12:00からの秒数

※FUnit: フォント内部で用いられる大きさの単位
Font Tables - TrueType Reference Manual - Apple Developer
データ読み込み用へルパメソッドのコードFontParser.cpp
FontParser::FontParser(const std::string& path) {  
  ifs.open(path, std::ios::binary);  
  if (!ifs) std::cerr << "failed to open file\n";
}

void FontParser::skipBytes(const unsigned bytes) {  
  ifs.seekg(bytes, std::ios::cur);  
}  
  
void FontParser::jumpTo(const unsigned byteOffset) {  
  ifs.seekg(byteOffset, std::ios::beg);  
}  
  
template <typename T>  
T FontParser::readBeOrThrow() {  
  uint32_t acc = 0;  
  for (std::size_t i = 0; i < sizeof(T); ++i) {  
    const int c = ifs.get();  
    if (c == EOF) throw std::runtime_error("unexpected EOF");  
    acc = (acc << 8) | static_cast<unsigned char>(c);  
  }  
  
  if constexpr (std::is_signed_v<T>) {  
    const auto bits = static_cast<unsigned>(sizeof(T) * 8);  
    const uint32_t sign_mask = (static_cast<uint32_t>(1) << (bits - 1));  
    if (acc & sign_mask) {  
      const uint64_t two_pow = static_cast<uint64_t>(1) << bits;  
      const int64_t signed_val =  
          static_cast<int64_t>(acc) - static_cast<int64_t>(two_pow);  
      return static_cast<T>(signed_val);  
    }  
    return static_cast<T>(acc);  
  } else {  
    return static_cast<T>(acc);  
  }  
}  
  
uint8_t FontParser::readUint8() { return readBeOrThrow<uint8_t>(); }  
uint16_t FontParser::readUint16() { return readBeOrThrow<uint16_t>(); }  
uint32_t FontParser::readUint32() { return readBeOrThrow<uint32_t>(); }  
int8_t FontParser::readInt8() { return readBeOrThrow<int8_t>(); }  
int16_t FontParser::readInt16() { return readBeOrThrow<int16_t>(); }  
int32_t FontParser::readInt32() { return readBeOrThrow<int32_t>(); }  
float FontParser::readF2Dot14() {  
  const auto raw = readBeOrThrow<int16_t>();  
  return static_cast<float>(raw) / static_cast<float>(1 << 14);  
}

 オフセットテーブルファイルを読み込むと、まずはテーブルディレクトリが現れます。ここにはttfに詰められたテーブルたちへアクセスするのに必要な情報が入っています。まずオフセットテーブルにテーブルディレクトリを読み込むためのデータが並び、 オフセットテーブルの最後のバイトのあとにテーブルディレクトリがnumTablesの数だけ続きます。


型
名前
説明


uint32
scaler type
OSX, iOS用のスケール

uint16
numTables
テーブルの数

uint16
searchRange
(maximum power of 2 <= numTables)*16

uint16
entrySelector
log2(maximum power of 2 <= numTables)

uint16
rangeShift
numTables*16-searchRange

https://developer.apple.com/fonts/TrueType-Reference-Manual/RM06/Chap6.html
テーブルディレクトリの構造です。ここに各テーブルへジャンプするためのオフセットが格納されているというわけです。これから各テーブルには何回もジャンプすることになるので、パーサーのフィールドにハッシュマップとして保存しておきましょう。


型
名前
説明


uint32
tag
テーブル名 (例: glyf)

uint32
checkSum
テーブルのチェックサム

uint32
offset
ファイル先頭からテーブル先頭へのオフセット(バイト)

uint32
length
テーブルサイズ(バイト)

テーブルディレクトリパーサーのコードFontParser.cpp
FontParser::FontParser(const std::string& path) {  
  ifs.open(path, std::ios::binary);  
  if (!ifs) std::cerr << "failed to open file\n";  
  
  // read header  
  skipBytes(sizeof(uint32_t)); // skip scaler type  
  const uint16_t numTables = readUint16();  
  // skip searchRange, entrySelector, rangeShift  
  skipBytes(sizeof(uint16_t) * 3);  
  
  // read table directory  
  for (int i = 0; i < numTables; ++i) {  
    constexpr unsigned bytesLength = 4;  
    char bytes[bytesLength + 1];  
    ifs.read(bytes, bytesLength);  
    bytes[bytesLength] = '\0';  
    const auto tag = std::string(bytes);  
    const auto checkSum = readUint32();  
    const auto offset = readUint32();  
    const auto length = readUint32();  
    directory[tag] = {checkSum, offset, length};  
  }  
}

 cmapテーブルテーブルへアクセスする手段を得たので、最初にcmapテーブルを見ていきます。繰り返しになりますがゴールはグリフのデータを得ることです。グリフはglyfテーブルに入っていますが、glyfテーブルへのアクセスはできても各グリフへのアクセスをする方法がまだありません。なので、これから文字コード -> GlyphCode(GlyphIndex) -> GlyphOffsetの順に変換する必要があります。（仕様書ではGlyphCodeとGlyphIndexが同じものを指す単語として現れますが、ここではこれ以降、統一してGlyphCodeを用います）そして最初の変換である、文字コードからGlyphCodeへのマッピングが保存されているのがcmapテーブルです。
cmapはインデックステーブル、サブテーブル、マッピングテーブルに分かれています。各サブテーブルはUnicode用、windows用など目的に応じて構造が異なります。今回の実装ではUnicodeのみサポートするので、どんなサブテーブルになるかを見てみると、format12とformat4の2つがあることがわかりました。そしてどうやら、モダンなUnicodeフォントでは大体format12を使っているようです。なので今回は一旦format12のみに対応することにします。ではテーブルの構造を見てみましょう。
cmapインデックステーブル


型
名前
説明


UInt16
version
バージョン番号(現在は0固定)

UInt16
numberSubtables
サブテーブルの数

cmap サブテーブル


型
名前
説明


UInt16
platformID
プラットフォーム識別子

UInt16
platformSpecificID
プラットフォーム特有のID

UInt32
offset
マッピングテーブルへのオフセット

cmap format 12マッピングテーブル


型
名前
説明


UInt16
format
サブテーブルフォーマット(12固定)

UInt16
reserved
予約済みエリア(0固定)

UInt32
length
ヘッダ含むこのサブテーブルのバイト長

UInt32
language
言語コード

UInt32
nGroups
グルーピングの数

グルーピング


型
名前
説明


UInt32
startCharCode
グループ最初のUnicode

UInt32
endCharCode
グループ最後のUnicode

UInt32
startGlyphCode
最初のGlyphCode 以降の文字は連続したGlyphCodeが割り当てられる

実装ではnumberSubtablesの数だけループを回し、グルーピングからUnicode -> GlyphCodeのマッピングを読み込めばOKです。グルーピングの構造が若干特殊で、単純な一対一のマッピングではなく、グループの最初と最後のUnicodeとGlyphCodeの先頭のみ与えられ、このUnicodeの範囲内は対応するGlyphCodeも一つずつ並んでいる、という仕組みになっています。実装を見てもらったほうがわかりやすいと思います。先程同様、ハッシュマップとして保存しておくと便利です。
Unicode → GlyphCodeのマッピングのコードFontParser.cpp
void FontParser::loadUnicodeToGlyphCodeMap() {  
  const auto cmapOffset = directory["cmap"].offset;  
  jumpTo(cmapOffset);  
  skipBytes(2); // skip version  
  const uint16_t numSubtables = readUint16();  
  
  u_int32_t subtableOffset = -1;  
  for (int i = 0; i < numSubtables; ++i) {  
    const auto platform = readUint16();  
    const auto encoding = readUint16();  
    const auto offset = readUint32();  
    // Only supports Unicode with format12 for now  
    // Ideally format4 should be supported for a fallback
    if (platform == 0 && encoding == 4) subtableOffset = offset;  
  }  
  
  if (subtableOffset == -1) {  
    throw std::runtime_error("Not supported format");  
  }  
  jumpTo(cmapOffset + subtableOffset);  
  
  // read subtable header to detect format  
  const uint16_t format = readUint16();  
  if (format == 12) {  
    skipBytes(10); // skip reserved, length, language  
    const uint32_t nGroups = readUint32();  
  
    for (int i = 0; i < nGroups; ++i) {  
      const auto startCharCode = readUint32();  
      const auto endCharCode = readUint32();  
      const auto startGlyphCode = readUint32();  
      unicodeToGlyphCode[startCharCode] = startGlyphCode;  
      const auto diff = (endCharCode - startCharCode);  
      for (int j = 1; j <= diff; ++j) {  
        unicodeToGlyphCode[startCharCode + j] = startGlyphCode + j;  
      }  
    }  
  } else {  
    throw std::runtime_error("Not supported format");  
  }  
}
https://developer.apple.com/fonts/TrueType-Reference-Manual/RM06/Chap6cmap.html

 locaテーブルGlyphCodeを取得できたら、対応するバイトオフセットを得ることでグリフにアクセスできます。そのマッピングがlocaテーブルに入っています。ラッキーなことにこのテーブルはかなりシンプルで、グリフのオフセットがGlyphCodeの順番に並んでいるだけです。ただしアンラッキーなことにlocaテーブルを読み始める前に必要なグリフの総数はmaxpテーブルのnumGlyphsに、オフセットの単位はheadテーブルのindexToLocFormatに散らばって保存されています。なんでよ…という気持ちを抑えて読みに行きます。実装ではlocaテーブルもハッシュマップにしておくとよいでしょう。


型
名前
説明


uint16
or
uint32
offsets[n]
グリフオフセット(バイト) 
※headテーブルindexToLocFormatが0の場合はそのまま、
1の場合は実際のオフセット/2

あと細かい点としては、グリフを持たないGlyphCodeの場合はオフセットが次のグリフと同じ値になります。グリフがないGlyphCodeって何だ？と思いましたがスペースなどがそれに当たるようです。なるほど！このチェックを入れてないと、例えばNotoSans JPだと"　"が"、"のオフセットに間違ってマッピングされてしまいます。
GlyphCode→GlyphOffsetマッピングのコードFontParser.cpp
void FontParser::loadGlyphOffsetsMap() {  
  jumpTo(directory["maxp"].offset + 4);  
  const int numGlyphs = readUint16();  
  
  jumpTo(directory["head"].offset);  
  skipBytes(50); // skip until indexToLocFormat  
  const auto isTwoByte = readInt16() == 0;  
  const auto glyphTableOffset = directory["glyf"].offset;  
  const auto locationTableOffset = directory["loca"].offset;  
  
  jumpTo(locationTableOffset);  
  for (int i = 0; i < numGlyphs; ++i) {  
    const auto glyphOffset = isTwoByte ? readUint16() * 2u : readUint32();  
    glyphCodeToOffset[i] = glyphTableOffset + glyphOffset;  
  }  
  // Remove offset for empty glyphs  
  for (int i = 1; i < numGlyphs; ++i) {  
    if (glyphCodeToOffset[i] == glyphCodeToOffset[i - 1]) {  
      glyphCodeToOffset[i - 1] = 0;  
    }  
  }  
}
https://developer.apple.com/fonts/TrueType-Reference-Manual/RM06/Chap6loca.html

https://developer.apple.com/fonts/TrueType-Reference-Manual/RM06/Chap6head.html

https://developer.apple.com/fonts/TrueType-Reference-Manual/RM06/Chap6maxp.html

 hhea, hmtxテーブルここまで読んでもらっている方に驚きはないかもしれませんが、レンダリングに必要な一部のグリフ情報はglyfテーブル以外にも散らばっています。特に重要なのがグリフの水平レイアウトに必要な幅のデータです。hheaテーブルにはフォント全体に対して、hmtxテーブルには各グリフに対してのサイズ関連データが入っています。単にグリフを横並びに配置して画像出力するだけなら、フォントの最大高さと各グリフの横幅がわかればよいです。高さはhheaテーブルのascent、descentに、グリフの横幅はhmtxテーブルに入っています。
hmtxテーブルはグリフIDごとの情報が配列に入っているが、配列の長さはhheaテーブルのNumberOfMetricsから取得する必要があります。なぜなら等幅フォントの場合グリフごとの情報は必要ないため、一つだけ提供されていたりいなかったりするためです。longHorMetricに入っているadvanceWidthはグリフの全体幅、leftSideBearing幅内でどれだけ左からシフトするかの値です。はhtmxテーブルのleftSideBearing[]はちょっと良く理解できなかったので一旦無視します… longHorMetricは以下のような構造になっています。
struct {
	uint16 advanceWidth;
	int16 leftSideBearing;
}
htmxテーブル


型
名前
説明


longHorMetric
hMetrics[numOfLongHorMetrics]
グリフのMetric

FWord
leftSideBearing[]
Here the advanceWidth is assumed to be the same as the advanceWidth for the last entry above. The number of entries in this array is derived from the total number of glyphs minus numOfLongHorMetrics. This generally is used with a run of monospaced glyphs (e.g. Kanji fonts or Courier fonts). Only one run is allowed and it must be at the end.

グリフmetricパーサーのコードFontParser.cpp
FontMetric FontParser::getFontMetric() {  
  jumpTo(directory["hhea"].offset);  
  skipBytes(4);  
  const auto ascent = readInt16();  
  const auto descent = readInt16();  
  return FontMetric{ascent, descent};  
}

  
void FontParser::loadGlyphMetricsMap() {  
  jumpTo(directory["hhea"].offset);  
  skipBytes(34); // Skip to numOfLongHorMetrics  
  const u_int16_t numOfMetrics = readUint16();  
  jumpTo(directory["hmtx"].offset);  
  for (int i = 0; i < numOfMetrics; ++i) {  
    const u_int16_t width = readUint16();  
    const int16_t lsb = readInt16();  
    glyphMetric[i] = Metric{width, lsb};  
  }  
}
https://developer.apple.com/fonts/TrueType-Reference-Manual/RM06/Chap6hhea.html

https://developer.apple.com/fonts/TrueType-Reference-Manual/RM06/Chap6hmtx.html
ここまででグリフデータを読み込むための準備ができました！

 レンダラーの準備グリフは簡単でもいいのでレンダリングできると圧倒的にテンションが上がります。なのでグリフデータを読み込み始める前に、簡単な2Dレンダラーを作っていきましょう。最初は点、直線、正方形を自由な場所に書き込めれば十分です。
簡単のために、フレームバッファと描写メソッドが一緒になったFrameBufferCanvasクラスを作ります。フレームバッファはピクセルごとのRGB情報を持った1次元配列とします。

まずは描写メソッドを作ります。点の描写はターゲットのピクセルを新しいRGBで更新。直線、正方形は点を与えられた区間に打ち続ければOKです。各点のx,y座標をバラバラに渡すのは後に面倒になるので、ベクトルを受け取れるオーバーロードも用意していると便利です。あとはレンダリング結果を画像にするため、stb-image-writerを使ってpngに出力するメソッドも作っておきます。
直線のアルゴリズムはBresenham’s line drawing - Playing with codeのものを借用しました。エンジニア全員やったほうが良い3Dレンダラー自作チュートリアルです。
FrameBufferCanvasのコードFrameBufferCanvas.cpp
struct RGB {  
  unsigned r, g, b;  
  RGB() = default;  
  
  constexpr RGB(const unsigned r_, const unsigned g_,  
                const unsigned b_) : r(r_), g(g_), b(b_) {  
  }  
  
  constexpr explicit RGB(const unsigned greyscale) : r(greyscale),  
    g(greyscale), b(greyscale) {  
  }  
  
  bool operator==(const RGB& a) const {  
    return r == a.r && g == a.g && b == a.b;  
  }  
};

FrameBufferCanvas::FrameBufferCanvas(const int width_,  
                                     const int height_) :  
  width(width_), height(height_) {  
  framebuffer = std::make_unique<RGB[]>(width * height);  
  for (int i = 0; i < width * height; ++i) framebuffer[i] = BLACK;  
}

void FrameBufferCanvas::set(const int x,  
                            const int y,  
                            const RGB color) {  
  if (x < 0 || y < 0) return;  
  if (x >= width || y >= height) return;  
  const std::size_t i = static_cast<std::size_t>(y) * static_cast<std::size_t>(  
                          width) + static_cast<std::size_t>(x);  
  framebuffer[i] = color;  
}

void FrameBufferCanvas::drawLine(int ax, int ay, int bx, int by,  
                                 const int thickness,  
                                 const RGB color) {  
  const int w = std::abs(ax - bx);  
  const int h = std::abs(ay - by);  
  const bool isSteep = w < h;  
  if (isSteep) {  
    std::swap(ax, ay);  
    std::swap(bx, by);  
  }  
  if (ax > bx) {  
    std::swap(ax, bx);  
    std::swap(ay, by);  
  }  
  auto y = static_cast<float>(ay);  
  for (int x = ax; x <= bx; ++x) {  
    if (isSteep) {  
      drawRect(static_cast<int>(y), x, thickness, thickness, color);  
    } else {  
      drawRect(x, static_cast<int>(y), thickness, thickness, color);  
    }  
    y += static_cast<float>(by - ay) / static_cast<float>(bx - ax);  
  }  
}  

void FrameBufferCanvas::drawRect(const int centerX,  
                                 const int centerY,  
                                 const int rectWidth,  
                                 const int rectHeight,  
                                 const RGB color) {  
  // compute integer bounds  
  const int halfW = rectWidth / 2;  
  const int halfH = rectHeight / 2;  
  int left = centerX - halfW;  
  int top = centerY - halfH;  
  int right = left + rectWidth;  
  int bottom = top + rectHeight;  
  
  // clip to framebuffer  
  if (right <= 0 || bottom <= 0) return;  
  if (left >= width || top >= height) return;  
  
  left = std::max(left, 0);  
  top = std::max(top, 0);  
  right = std::min(right, width);  
  bottom = std::min(bottom, height);  
  
  for (int y = top; y < bottom; ++y) {  
    for (int x = left; x < right; ++x) {  
      set(x, y, color);  
    }  
  }  
}

void FrameBufferCanvas::writePngFile(const char* fileName) const {  
  stbi_write_png(fileName, width, height, 3, framebuffer.get(), 0);  
}
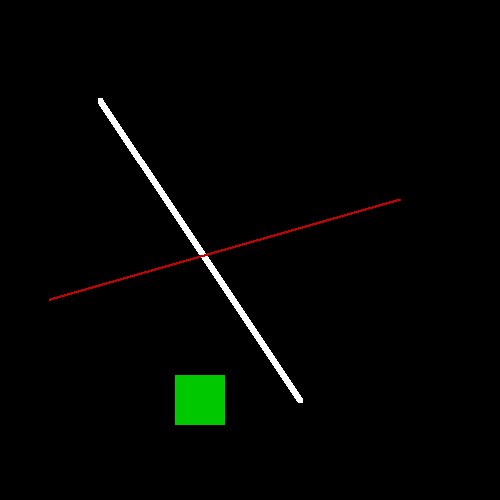
int main() {  
  FrameBufferCanvas canvas{500, 500};  
  canvas.drawLine(100, 100, 300, 400, 5, {255, 255, 255});  
  canvas.drawLine(400, 200, 50, 300, 2, {200, 0, 0});  
  canvas.drawRect(200, 400, 50, 50, {0, 200, 0});  
  canvas.writePngFile("out.png");  
}
これでグリフを描写する準備ができました。

 グリフのパース & アウトラインの描写それでは本丸、グリフのパースを行っていきます。グリフの情報はglyfテーブルに入っています。グリフにはSimple glyphとCompound glyphの二種類ありますが、Compound glyphは複数のグリフを内包したグリフなため、一旦Simple glyphを読み込むことを目標に進めていきましょう。

 glyfテーブルのパースその他のテーブル同様、glyfテーブルもヘッダと本体の二箇所に分かれています。ヘッダ部で重要な情報はnumberOfContours、輪郭数です。ここが正ならSimple glyphの輪郭数、負ならCompound glyphというように分岐します。
グリフヘッダテーブル


型
名前
説明


int16
numberOfContours
輪郭の数
プラスならSimple glyph
マイナスならCompound glyph

FWord
xMin
x座標最小値

FWord
yMin
y座標最小値

FWord
xMax
x座標最大値

FWord
yMax
y座標最大値


 Simple glyph本体です。ついにグリフのレンダリングに必要な情報が出てきました！輪郭の最後の点は輪郭の数だけあり、その他の配列は頂点の数だけあるのが注意点です。頂点の数は明示されていませんが、endPtsOfContoursの最大値を取ればOKです。インストラクションは今回の実装では無視します。
Simple glyphテーブル


型
名前
説明


uint16
endPtsOfContours[n]
輪郭の最後の点のインデックスの配列(n=輪郭数)

uint16
instructionLength
インストラクションの長さ

uint8
instructions[instructionLength]
インストラクション

uint8
flags[variable]
フラグの配列(n=頂点数)

uint8 or int16
xCoordinates[]
x座標(n=頂点数)

uint8 or int16
yCoordinates[]
y座標(n=頂点数)

ややこしいのがフラグです。いくつかのフラグは他のフラグの挙動を分岐させます。具体的には1,2,4,5ビットの挙動が以下のようになっています。
3がセットされていたら次のバイトで示された数分だけ同じフラグを使用する
1,2と4,5はそれぞれx, yの座標を得るためのフラグ
1,2がセットされていたら、対応する座標の長さは1byte(unsigned)、そうでなければ2bytes(signed)
1,2がセットされているとき、4,5は符号になる
1,2がセットされておらず、4.5がセットされていれば、一つ前の座標位置と同じ
1,2がセットされておらず、4,5もセットされていなければ、2bytes(signed int)が座標位置
On Curveはベジエ曲線を描写するにあたって必要な情報です。後ほど曲線のレンダリングで説明します。Repeatがセットされているときは、すぐ次の16ビットに格納されている数のぶんだけ同じフラグをリピートします。


フラグ
ビット
説明


On Curve
0
オン: 曲線の上
オフ: 曲線の外

x-Short Vector
1
オン: x座標が1バイト
オフ: x座標が2バイト

y-Short Vector
2
オン: y座標が1バイト
オフ: y座標が2バイト

Repeat
3
オン: 次の1バイトに入っている数だけ同じフラグが続く
オフ: リピートしない

This x is same (Positive x-Short vector)
4
オン: 2がオンならx座標がプラス、2がオフなら一つ前のx座標と同じ
オフ: 2がオンならx座標がマイナス、2がオフならx座標は次のuint16

This y is same (Positive y-Short vector)
5
オン: 2がオンならx座標がプラス、2がオフなら一つ前のy座標と同じ
オフ: 2がオンなら6座標がマイナス、2がオフならy座標は次のuint16

Reserved
6 - 7
使用されていない

実装です。グリフには二種類ありますが、GlyphがGlyphComponentを0個以上持つ、という構造にすることで、2種類のグリフで同じ構造を使うことができます。よって実装上、Simple glyphはGlyphComponentを0か1つ持つGlyphになります。getGlyphComponentについてaffineMatを受け取っていますが、これはComponent Glyph用なのでSimple glyphでは単位行列を渡していればOKです。
GlyphとGlyphComponentのヘッダGlyph.h
struct Metric {  
  uint16_t advanceWidth;  
  int16_t leftSideBearing;  
};

class Glyph {  
public:  
  Glyph() = default;  
  explicit Glyph(std::vector<GlyphComponent> components_, Metric metric_);  
  [[nodiscard]] const std::vector<GlyphComponent>& getComponents() const;  
  [[nodiscard]] const Metric& getMetric() const;
  static Glyph EmptyGlyph(Metric metric_);
  
private:  
  std::vector<GlyphComponent> components;  
  Metric metric;  
};
GlyphComponent.h
class GlyphComponent {  
public:  
  GlyphComponent() : numOfVertices(0) {  
  }  
  
  explicit GlyphComponent(uint16_t numOfVertices_,  
                          std::unordered_set<uint16_t> endPtsOfContours_,  
                          std::unordered_set<uint16_t> ptsOnCurve_,  
                          BoundingRect boundingRect_,  
                          std::vector<glm::vec2> coordinates_);  
  [[nodiscard]] uint16_t getNumOfVertices() const;  
  [[nodiscard]] BoundingRect getBoundingRect() const;  
  [[nodiscard]] const std::unordered_set<uint16_t>& getEndPtsOfContours() const; 
  [[nodiscard]] const std::unordered_set<uint16_t>& getPtsOnCurve() const;  
  [[nodiscard]] const std::vector<glm::vec2>& getCoordinates() const;  
  
private:  
  uint16_t numOfVertices;  
  std::unordered_set<uint16_t> endPtsOfContours;  
  BoundingRect boundingRect;  
  std::vector<glm::vec2> coordinates;  
  std::unordered_set<uint16_t> ptsOnCurve;  
};
Simple GlyphパーサーのコードFontParser.cpp
Glyph FontParser::getGlyph(const uint32_t cp) {  
  if (!unicodeToGlyphCode.contains(cp)) {  
    throw std::runtime_error("Glyph not found");  
  }  
  return getGlyphByCode(unicodeToGlyphCode[cp]);  
}

Glyph FontParser::getGlyphByCode(const uint16_t glyphCode) {  
  const auto [numOfContours, boundingRect] = readGlyphHeader(glyphCode);  
  Glyph glyph;  
  const auto metric = glyphMetric[glyphCode];  
  if (numOfContours == 0) {  
    // No glyph needed i.e. space  
    glyph = Glyph::EmptyGlyph(metric);  
  } else if (numOfContours > 0) {  // Read simple glyphs  
    glyph = Glyph({getGlyphComponent(numOfContours, boundingRect)},  
                  metric);  
  } else {  
    glyph = getCompoundGlyph(); // Not implemented yet!
  }  
  return glyph;  
}

GlyphHeader FontParser::readGlyphHeader(const uint16_t glyphCode) {  
  const auto offset = glyphCodeToOffset[glyphCode];  
  if (offset == 0) {  
    return GlyphHeader{0, BoundingRect{0, 0, 0, 0}};  
  }  
  
  jumpTo(offset);  
  // Read glyph description  
  const auto numOfContours = readInt16(); // number of contours  
  BoundingRect boundingRect;  
  boundingRect.xMin = readInt16();  
  boundingRect.yMin = readInt16();  
  boundingRect.xMax = readInt16();  
  boundingRect.yMax = readInt16();  
  
  return GlyphHeader{numOfContours, boundingRect};  
}

GlyphComponent FontParser::getGlyphComponent(  
    const int16_t numOfContours,  
    const BoundingRect boundingRect,  
    const glm::mat3& affineMat) {  
  std::unordered_set<uint16_t> endPtsOfContours;  
  
  uint16_t numOfVertices = 1;  
  for (int i = 0; i < numOfContours; ++i) {  
    const auto point = readUint16();  
    numOfVertices = std::max(numOfVertices, static_cast<uint16_t>(point + 1));  
    endPtsOfContours.insert(point);  
  }  
  // Skip instructions  
  skipBytes(readUint16());  

  std::vector<uint8_t> allFlags(numOfVertices, 0);  
  std::unordered_set<uint16_t> ptsOnCurve;  
  uint16_t idx = 0;  
  while (idx < numOfVertices) {  
    const uint8_t f = readUint8();  
    allFlags[idx] = f;  
    //ON_CURVE_POINT  
    if (isFlagSet(f, 0)) ptsOnCurve.insert(idx);
    if (isFlagSet(f, 3)) {  
      // REPEAT_FLAG  
      const uint8_t repeat = readUint8();
      // fill repeats      
      for (uint16_t r = 1; r <= repeat; ++r) allFlags[idx + r] = f;  
      idx += static_cast<uint16_t>(repeat) + 1;  
    } else {  
      ++idx;  
    }  
  }  
  
  const std::vector<int> xCoordinates = getGlyphCoordinates(  
      numOfVertices, allFlags, true);  
  const std::vector<int> yCoordinates = getGlyphCoordinates(  
      numOfVertices, allFlags, false);  
  std::vector<glm::vec2> coordinates;  
  for (int i = 0; i < numOfVertices; ++i) {  
    const auto coord = affineMat * glm::vec3(xCoordinates[i], yCoordinates[i],  
                                             1);  
    coordinates.emplace_back(coord.x, coord.y);  
  }  
  
  return GlyphComponent{numOfVertices, endPtsOfContours, ptsOnCurve,  
                        boundingRect, coordinates};  
}

std::vector<int> FontParser::getGlyphCoordinates(const uint16_t& n,  
                                                 const std::vector<uint8_t>&  
                                                 flags,  
                                                 const bool isX) {  
  std::vector coordinates(n, 0);  
  for (int i = 0; i < n; ++i) {  
    const auto f = flags[i];  
    const auto isShort = isFlagSet(f, isX ? 1 : 2);  
    int pos = coordinates[i == 0 ? 0 : i - 1];  
  
    if (isShort) {  
      const auto isPositive = isFlagSet(f, isX ? 4 : 5);  
      const auto offset = isPositive  
                            ? readUint8()  
                            : -1 * static_cast<int>(readUint8());  
      pos += offset;  
    } else {  
      if (!isFlagSet(f, isX ? 4 : 5)) {  
        pos += readInt16();  
      };  
    }  
  
    coordinates[i] = pos;  
  }  
  return coordinates;  
}

 アウトラインを直線でレンダリングそれではグリフをパースして得たx,y座標を直線で繋いでみましょう。グリフの座標は直交座標系ですが、フレームバッファは左上が原点の画像座標系なので座標変換を行う必要があります。ここでは一旦出力画像を上下反転しちゃいましょう。ちゃんとした座標変換は後ほど扱います。
グリフのアウトラインを直線でレンダリングするコードFrameBufferCanvas.cpp
void FrameBufferCanvas::renderGlyphOutline(const unsigned int startX,  
                                    const unsigned int startY,  
                                    const Glyph& glyph,  
                                    const RGB color) {  
  for (const auto& c : glyph.getComponents()) {  
    uint16_t contourStartPt = 0;  
    const auto n = c.getNumOfVertices();  
    const auto coordinates = c.getCoordinates();  
    const auto endPtsOfContours = c.getEndPtsOfContours();  
  
    for (int i = 0; i < n; ++i) {  
      const auto isEndPt = endPtsOfContours.contains(i);  
      const auto nextIdx = isEndPt ? contourStartPt : (i + 1) % n;  
      const auto x = coordinates[i].x + startX;  
      const auto y = coordinates[i].y + startY;  
      const auto nextX = coordinates[nextIdx].x + startX;  
      const auto nextY = coordinates[nextIdx].y + startY;  
      drawLine(x, y, nextX, nextY, 5, color);  
      drawRect(x, y, 20, 20, color);  
      if (isEndPt) contourStartPt = i + 1;  
    }  
  }  
    stbi_flip_vertically_on_write(1);
}
main.cpp
int main() {  
  FontParser parser("fonts/JetBrainsMono-Bold.ttf");  
  FrameBufferCanvas canvas{1200, 1200};  
  const auto cps = utf8ToCodepoints("a");
  const Glyph glyph = parser.getGlyph(cps[0]);  
  canvas.renderGlyphOutline(300, 300, glyph, RGB{255});  
  canvas.writePngFile("out.png");  
}
輪郭がレンダリングできました！まだカクカクしてますが、ここまででも十分感動的だと思いませんか？

 Compound glyphSimple glyphのデータを無事読み込めたなら、それはCompound glyphを扱う準備ができたということです。Compound glyphのアイデア自体は"o"と"ö"、"i"と"j"のようにグリフの一部が同じ形なら、その部分は共通化できるよね、という単純なものです。ただし、グリフを組み合わせるには最終的にできるグリフの中での各要素の位置やサイズ、変形方法を指定する必要があります。それを考慮しないと、以下のような結果になります。


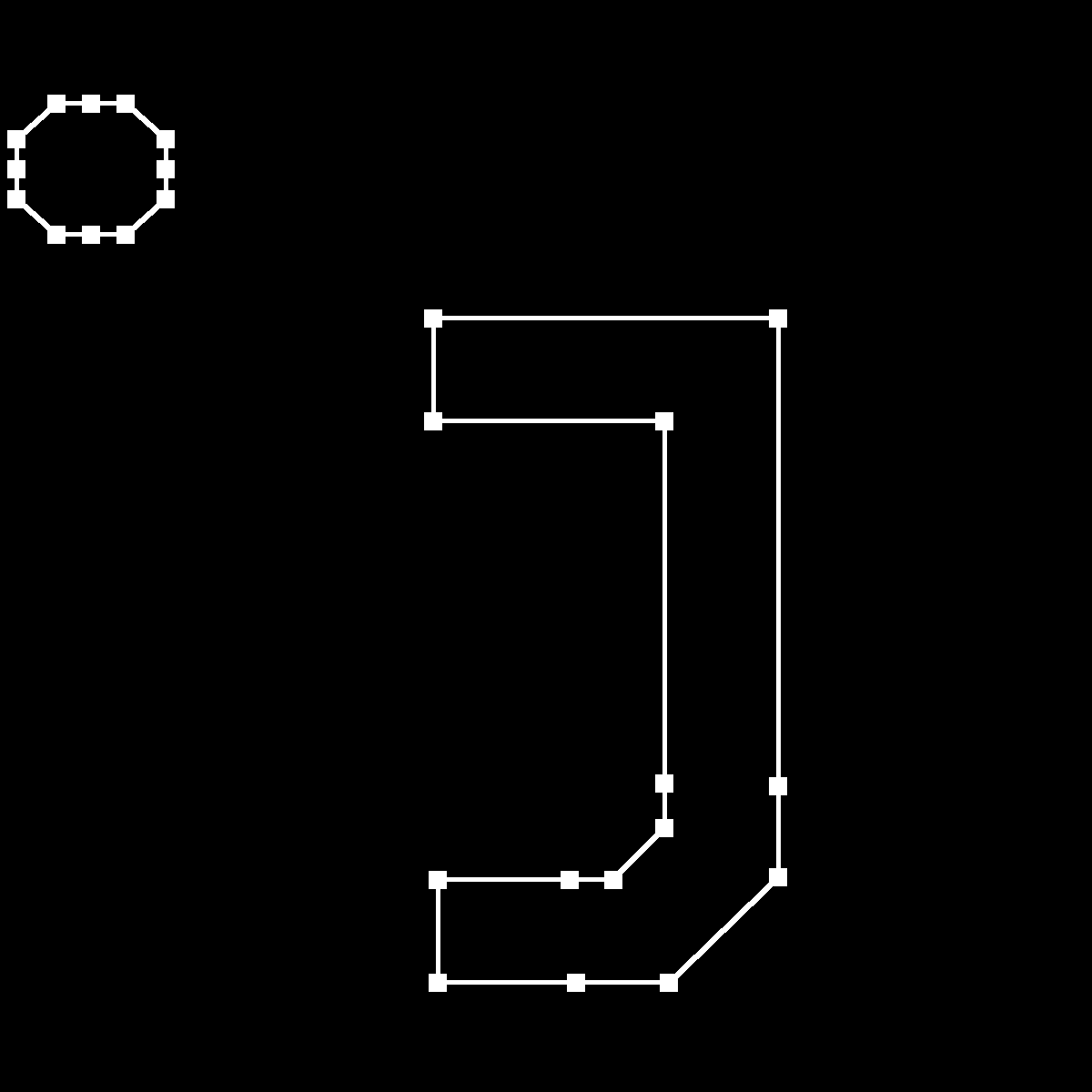
点があらぬ場所にある、jになるはずだったもの
それではCompound glyphのデータをパースしていきます。ここがパーサーで最もややこしいですが、ゆっくり追えば理解できるはずです！
Glyphのヘッダ部はSimple glyphと共通で、numberOfContoursが負のときに本体部分がCompound glyphのものになります。Compound glyph自体にはグリフの座標情報などは入っておらず、Compoundの中に複数のComponent glyphが入っている入れ子構造になっています。そのComponentはSimple glyph, Compound glyphのどちらも取りうるのですが、Simple glyphしか具体的な座標情報を持っていないことから、最終的にはSimple glyphに行き着くようになっています。なので複数のComponentsを取り出して、変形して、合体する必要があるということです。
基本的にはComponentを変形するための式を構築します。どのような式になるのかはフラグによって変わります。そしてそのフラグが多く10個もありますが、この記事ではARGS_ARE_XY_VALUES, ROUND_XY_TO_GRID, WE_HAVE_INSTRUCTIONS, OVERLAP_COMPOUNDの4つは無視することにします。

ここで大事な情報はどうやってこのComponentを変形、移動するかです。仕様書には以下の式が書かれています。

\begin{aligned}
x' &= m\left( \frac{a}{m}x + \frac{c}{m}y + e \right) \\
y' &= n\left( \frac{b}{n}x + \frac{d}{n}y + f \right)
\end{aligned}
a,b,c,dはフラグによって以下のように定義され、データはパーツテーブルの次に入っています。ここでa,b,c,dはF2Dot14型であることに注意してください。


WE_HAVE  
_A_SCALE
WE_HAVE  
AN_X_AND  
Y  
SCALE
WE_HAVE_A  
TWO_BY  
TWO
a
b
c
d


0
0
0
1.0
0.0
0.0
1.0

1
0
0
1st short
0.0
0.0
1st short

0
1
0
1st short
0.0
0.0
2nd short

0
0
1
1st short
2nd short
3rd short
4th short

e,fにはARGS_ARE_XY_VALUESが常にオンと仮定すると変数1, 変数2がそのまま入ります。

そしてWE_HAVE_A_SCALE, WE_HAVE_AN_X_AND_Y_SCALE, WE_HAVE_A_TWO_BY_TWOと先ほどの変数、追加で読み込むいくつかの値によって行列が決定されます。このフラグたちは排他的で同時に複数がオンになることはありません。上のテーブルを読み解くと、各フラグに応じて以下のような変形が行われることがわかります。
WE_HAVE_A_SCALE: x,yで同じ拡大
WE_HAVE_AN_X_AND_Y_SCALE scale: x,yで異なる拡大
WE_HAVE_A_TWO_BY_TWO: 線形変換用の行列がまるっと与えられる
最後に、mはm₀ = max(|a|, |b|), If |(|a|-|c|)| ≤ 33/65536, then m = 2m₀; otherwise, m = m₀で定義され、nについても同様です。
この先は点や線をベクトルで表現していくので、変換を簡単にするために取り出した変数と与えられた式をもとにアフィン変換用の行列をつくりましょう。

\begin{bmatrix}
x' \\
y' \\
1
\end{bmatrix}
=
\begin{bmatrix}
a & c & m e \\
b & d & n f \\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
x \\
y \\
1
\end{bmatrix}
行列が完成したのでGlyphComponentを取得するメソッドに渡して、帰ってきたGlyphからComponentを取り出し組み合わせればよいということです。最終的なグリフのMetricはUSE_MY_METRICSがオンのComponentのものを使います。

この一連をMORE_COMPONENTSがオンの限りループして合成していき、最終的なCompound glyphの完成です！
Component glyphパーツテーブル


型
名前
説明


uint16
flags
フラグ

uint16
glyphIndex
読み込み先のGlyphCode

int16, uint16, int8 or uint8
argument1
変数1 フラグによって内容が変わる

int16, uint16, int8 or uint8
argument2
変数2 フラグによって内容が変わる

transformation option

変形オプション

flagsの内容


フラグ
ビット
説明


ARG_1_AND_2_ARE_WORDS
0
オン: 変数1の型がWord
オフ: Byte

ARGS_ARE_XY_VALUES
1
オン: 変数はx,y座標
オフ: アンカーポイント

ROUND_XY_TO_GRID
2
ビット1がオンのときだけ読む
オン: x,yをグリッドに合わせて丸める
オフ: 丸めない

WE_HAVE_A_SCALE
3
オン: 後に与えられる値でスケールする
オフ: スケール値を1とする

(this bit is obsolete)
4
使われていないフラグ

MORE_COMPONENTS
5
オン: この次にまだComponentがある
オフ: もうない

WE_HAVE_AN_X_AND_Y_SCALE
6
オン: x座標のスケールがy座標と異なる
オフ: x,yどちらも同じスケーリング

WE_HAVE_A_TWO_BY_TWO
7
オン: 線形変換用の2x2行列が与えられる
オフ: 与えられない

WE_HAVE_INSTRUCTIONS
8
オン: インストラクションがある
オフ: ない

USE_MY_METRICS
9
オン: このComponentのmetricをCompound glyphのmetricとする
オフ: しない

OVERLAP_COMPOUND
10
オン: このCompound glyphはcomponentsがオーバーラップしてできている
オフ: オーバーラップがない

実装です。Compound glyphが入れ子になっているため再帰を使うと簡単になると思います。
Compound GlyphパーサーのコードFontParser.cpp
std::vector<GlyphComponent> FontParser::getCompoundSubComponents(  
    const uint16_t glyphCode,  
    const glm::mat3& affineMat) {  
  const auto [numOfContours, boundingRect] = readGlyphHeader(glyphCode);  
  std::vector<GlyphComponent> components;  
  if (numOfContours > 0) {  
    // Simple  
    components.emplace_back(  
        getGlyphComponent(numOfContours, boundingRect, affineMat));  
  } else {  
    // Compound: Compound glyph can have nested Compound glyphs  
    const auto subComponents = getCompoundGlyph().getComponents();  
    components.insert(components.begin(), subComponents.begin(),  
                      subComponents.end());  
  }  
  return components;  
}

Glyph FontParser::getCompoundGlyph() {  
  std::vector<GlyphComponent> components;  
  uint16_t flags;  
  Metric metric{};  
  do {  
    flags = readUint16();  
    const uint16_t glyphCode = readUint16();  
    // read flags  
    const bool isWord = isFlagSet(flags, 0);  
    const bool isXyValue = isFlagSet(flags, 1); // not implemented  
    const bool roundXyGrid = isFlagSet(flags, 2); // not implemented  
    const bool hasScale = isFlagSet(flags, 3);  
    const bool hasXScale = isFlagSet(flags, 6);  
    const bool hasTwoByTwo = isFlagSet(flags, 7);  
    const bool hasInstruction = isFlagSet(flags, 8); // not implemented  
    const bool useMetrics = isFlagSet(flags, 9);  
    const bool overlap = isFlagSet(flags, 10); // not implemented  
  
    // read arguments (arg1,arg2) either words or bytes (signed)    
    int32_t arg1 = 0, arg2 = 0;  
    if (isWord) {  
      arg1 = readInt16();  
      arg2 = readInt16();  
    } else {  
      arg1 = static_cast<int32_t>(static_cast<unsigned char>(readInt8()));  
      arg2 = static_cast<int32_t>(static_cast<unsigned char>(readInt8()));  
    }  
    // interpret arg1/arg2 later: XY values  
    const int32_t e_raw = arg1;  
    const int32_t f_raw = arg2;  
  
    // read transform values only when indicated  
    double a = 1.0, b = 0.0, c = 0.0, d = 1.0;  
    if (hasScale) {  
      const double s = readF2Dot14();  
      a = d = s;  
      b = c = 0.0;  
    } else if (hasXScale) {  
      a = readF2Dot14();  
      d = readF2Dot14();  
      b = c = 0.0;  
    } else if (hasTwoByTwo) {  
      a = readF2Dot14();  
      b = readF2Dot14();  
      c = readF2Dot14();  
      d = readF2Dot14();  
    } // else identity  
  
    // Normalization factors    constexpr float eps = 33.0 / 65536.0;  
    float m = static_cast<float>(std::max(std::fabs(a), std::fabs(b)));  
    m = std::fabs(a) - std::fabs(c) <= eps ? 2 * m : m;  
    float n = static_cast<float>(std::max(std::fabs(c), std::fabs(d)));  
    n = std::fabs(b) - std::fabs(d) <= eps ? 2 * n : n;  
    const auto e = static_cast<float>(e_raw);  
    const auto f = static_cast<float>(f_raw);  
  
    // The affine transformation matrix, looks like this:  
    // [a, c, me]    
    // [b, d, nf]    
    // [0, 0,  1]    
    const auto affineMat = glm::mat3(a, b, 0, c, d, 0, m * e, n * f, 1);  
  
    // Needs to save the current reader pos since getGlyph jumps to a certain offset pos  
    const auto currentOffset = ifs.tellg();  
    const auto subComponents =  
        getCompoundSubComponents(glyphCode, affineMat);  
    if (subComponents.empty()) {  
      throw std::runtime_error(  
          "FontParser: Something went wrong with loading component glyphs");  
    }  
    components.insert(components.end(), subComponents.begin(),  
                      subComponents.end());  
  
    if (useMetrics) {  
      metric = glyphMetric[glyphCode];  
    }  
    // Reload the prev reader pos for the next loop  
    jumpTo(currentOffset);  
  } while (isFlagSet(flags, 5)); // MORE_COMPONENTS  
  
  return Glyph(components, metric);  
}
これで最低限のTrueTypeパーサーが完成しました。"j"もちゃんとレンダリングされています！


点を取り戻したjくん
https://developer.apple.com/fonts/TrueType-Reference-Manual/RM06/Chap6glyf.html

 レンダラー　曲線の描写次はレンダラーを改善していきましょう。まずは曲線を描写したいですね。

 ベジエ曲線の定義ベジエ曲線は多くのベクターグラフィックで用いられている、数式で表されるなめらかな曲線です。ベクターグラフィックスエディタでよく見かけると思います。Pが各制御点の座標、tがパラメータです。Pの最初と最後がベジエ曲線の端点になります。

B(t) = \sum_{i=0}^{n} \binom{n}{i} (1 - t)^{n - i} t^i P_i, \quad 0 \le t \le 1
先述の通り、TrueTypeの曲線は二次ベジエ曲線で表されます。よって上の式を展開すると、以下のようになります。

B(t) = (1 - t)^2 P_0 + 2(1 - t)t P_1 + t^2 P_2, \quad 0 \le t \le 1
余裕のある方は以下のオンラインブックを読んでみると良いと思います。

https://pomax.github.io/bezierinfo/ja-JP/index.html

 ド・カステリョのアルゴリズムここで、ベジエ曲線には「制御点をt: t-1に繰り返し内分することで得られる」というありがたい性質があります。つまりは線形補間(=lerp)を次数だけ繰り返せばよいということです。これをド・カステリョのアルゴリズムと呼びます。
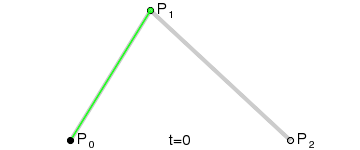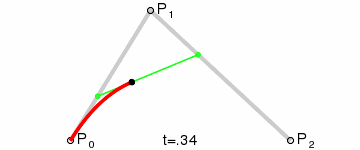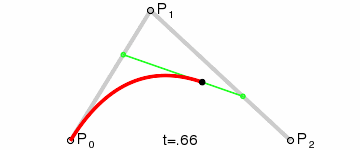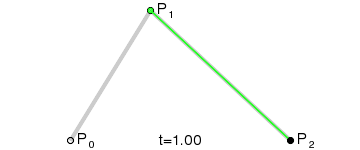
コードに起こしてみるとこうなります。
Geometry.h
inline glm::vec2 lerp(const glm::vec2& a, const glm::vec2& b, const float t) {  
  assert(t >= 0 && t <= 1);  
  return a + (b - a) * t;  
}  
  
inline glm::vec2  
bezierLerp(const glm::vec2& a, const glm::vec2& b, const glm::vec2& c,  
           const float t) {  
  assert(t >= 0 && t <= 1);  
  return lerp(lerp(a, b, t), lerp(b, c, t), t);  
}

 TrueTypeのベジエ曲線グリフをパースしたとき、Simple Glyphの各点にON_CURVE_POINTフラグがあったのを覚えていますか？実はこのフラグが曲線の端点かどうかを表す値だったのです。フラグがオンのとき、ベジエ曲線のカーブ上にある、つまり線分の端点で、オフのときは端点以外の制御点になります。

このセクションの以降の説明では、簡単のために端点をA, それ以外の制御点をBとおきます。

AとBがどんな役割か分かったところで、Aを白、Bを緑にしてアウトラインをレンダリングしてみましょう。
レンダリング結果を眺めていると、ある違和感に気づくかもしれません。Bが2つ以上並んでいる箇所があります！これは二次ベジエ曲線では本来ありえませんが、実はTrueTypeでは暗黙の端点が用いられているため発生しているのです。具体的には以下の２つのパターンによって2次ベジエ曲線が作られます。
"A-B-A" の並びの場合、そのまま2次ベジエ曲線になる
"B-B"と続く並びの場合、２つのBの中点にAがあると仮定して、2次ベジエ曲線を作る
これを踏まえて、B２つが並んだ場合の暗黙の端点を青で出力すると以下のようになります。（見やすさのために曲線部分のアウトラインは非表示にしています）
ちゃんと曲線部では端点とそれ以外が交互に現れていますね！それでは以上を踏まえて実装用にフローを整理しましょう。
ひとつ前に描写につかったAはループ外に保持し、描写後に更新していく (\text{prev}A)
今見ている点がAかつ次もAなら、直線を描写
今見ている点がBかつ...
グリフデータ上の次の点もBなら、描写用の次の端点A^\primeを用意し、\text{prev}A-B-A^\primeでベジエ曲線を描写
グリフデータ上の次の点がAなら、\text{prev}A-B-Aでベジエ曲線を描写

ちょうどよいので、ここで座標変換用のアフィン変換行列を用意して、グリフの開始x座標も簡単に渡せるようにしましょう。まずは座標系をx軸に対して反転させる行列を作っておいて、後からベースラインとグリフのx座標を調整できるようにします。

\begin{bmatrix}
x' \\
y' \\
1
\end{bmatrix}
=
\begin{bmatrix}
1 & 0 & \text{start x pos} \\
0 & -1 & \text{baseline} \\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
x \\
y \\
1
\end{bmatrix}
ベジエ曲線の処理を加えたアウトラインレンダラーのコードvoid FrameBufferCanvas::setGlyphBaseline(const int baseline) {  
  transformMat[2][1] += baseline;  
}

void FrameBufferCanvas::renderGlyphOutline(const Glyph& glyph,  
                                           const RGB color,  
                                           const int startX,  
                                           const int thickness) {  
  for (const auto& c : glyph.getComponents()) {  
    const auto rectSize = thickness * 2;  
    uint16_t contourStartPt = 0;  
    const auto n = c.getNumOfVertices();  
    const auto coordinates = c.getCoordinates();  
    const auto endPtsOfContours = c.getEndPtsOfContours();  
    const auto ptsOnCurve = c.getPtsOnCurve();  
  
    transformMat[2][0] = startX;  
  
    // Cache of point vectors of vertices  
    std::unordered_map<int, glm::vec2> points;  
    for (int i = 0; i < n; ++i) {  
      // Convert coordinate system from bottom-up to top-down  
      points[i] = transformVec2(transformMat, coordinates[i]);  
    }  
  
    auto prevPt = glm::vec2(0.f);  
    for (int i = 0; i < n; ++i) {  
      const auto isEndPt = endPtsOfContours.contains(i);  
      const auto nextIdx = isEndPt ? contourStartPt : (i + 1) % n;  
      const auto isOnCurve = ptsOnCurve.contains(i);  
      const auto isNextOnCurve = ptsOnCurve.contains(nextIdx);  
      // Convert coordinate system from bottom-up to top-down  
      auto currentPt = points[i];  
      auto nextPt = points[nextIdx];  
  
      if (isOnCurve) {  
        if (isNextOnCurve) {  
          drawLine(currentPt, nextPt, thickness, color);  
        }  
        prevPt = currentPt;  
      } else {  
        if (!isNextOnCurve) {  
          // Calculate the implicit next "on-curve" from the middle point of next control point  
          nextPt = (currentPt + nextPt) / 2.0f;  
        }  
        drawBezier(prevPt, currentPt, nextPt, thickness, color);  
        // Draw implicit next on-curve point  
        drawRect(nextPt, rectSize, rectSize, BLUE);  
        prevPt = nextPt;  
      }  
      drawRect(currentPt, rectSize, rectSize, isOnCurve ? RED : GREEN);  
      if (isEndPt) contourStartPt = i + 1;  
    }  
  }  
}

  
void FrameBufferCanvas::drawBezier(const glm::vec2& startPt,  
                                   const glm::vec2& midPt,  
                                   const glm::vec2& endPt,  
                                   const int thickness,  
                                   const RGB color) {  
  // approximate curve length  
  const float approxLen = glm::length(midPt - startPt) + glm::length(  
                              endPt - midPt);  
  const int res = std::max(1, static_cast<int>(std::ceil(approxLen)));  
  
  glm::vec2 last = startPt;  
  for (int i = 1; i <= res; ++i) {  
    const float t = static_cast<float>(i) / static_cast<float>(res);  
    glm::vec2 cur = quadBezierLerp(startPt, midPt, endPt, t);  
    drawLine(last, cur, thickness, color);  
    last = cur;  
  }  
}
これでアウトラインまでレンダリングできました！
https://developer.apple.com/fonts/TrueType-Reference-Manual/RM01/Chap1.html#contours

 レンダラー　グリフの塗りつぶし最後の関門、塗りつぶしです。TrueTypeにはグリフのアウトラインのデータまでしか無く、塗りつぶし方法は各レンダラーの実装次第になっています。今回はベクターデータの塗りつぶし方式として一般的な、Even-odd法とNon-zero法の二種類を実装してみます。


左: Even-odd法での塗りつぶし 右: Non-zero法での塗りつぶし

 Even-odd法任意の点から任意の方向に直線（スキャンライン）を引き、その直線が図形の輪郭と交わった回数が偶数回なら塗らない、奇数回なら塗る、というシンプルなアルゴリズムです。したがって、直線と線分、直線と曲線が交差する点を返す関数を作れば良いということです。

 線分の交点線分の交差判定は領域を使うと少し楽ですね。線分A_1A_2 とB_1B_2の判定を行うとすると、A_1A_2からなる直線を境界線としたとき、B_1とB_2が違う領域にあって、直線B_1B_2を境界線としたときA_1とA_2が違う領域にあれば線分が交差していると言えます。式に起こしていきましょう。

直線A_1A_2の式は以下で表されます。

f(x) = y = \frac{A_{2y} - A_{1y}}{A_{2x} - A_{1x}} (x - A_{1x}) + A_{1y}
これを変形して、x, yを入れたら領域を返す関数にします。

f(x,y) = (A_{2y} - A_{1y})(x - A_{1x}) - (A_{2x} - A_{1x})(y - A_{1y})
交点があることがわかったら、ベクトルを用いて交点の座標を求めます。

\begin{aligned}
V_1 &= A_2 - A_1 \\
V_2 &= B_2 - B_1
\end{aligned}
とおくと、A_1とA_2の間の任意の点A(t)、同じくB(t)は以下の式で表されます。

\begin{aligned}
A(t) &= A_1 + t V_1 \\
B(u) &= B_1 + u V_2
\end{aligned}
よって、A(t) = B(u)を満たすようなtもしくはuを見つければ良いということです。二次元での外積を使えばuを消せるので楽に計算できます。

\begin{aligned}
t V_1 - u V_2 &= B_1 - A_1 \\
t V_1 \times V_2 - u V_2 \times V_2 &= (B_1 - A_1) \times V_2 \\
t &= \frac{(B_1 - A_1) \times V_2}{V_1 \times V_2}
\end{aligned}
ふたつの線分の交点を求めるコードGeometry.h
inline std::optional<glm::vec2> segmentsIntersect(  
    const glm::vec2& a1, const glm::vec2& a2,  
    const glm::vec2& b1, const glm::vec2& b2) {  
  //  >0: c is above of start-end line, <0: below, ==0: on the line  
  const auto region = [](const glm::vec2& pt, const glm::vec2& start,  
                         const glm::vec2& end) {  
    return (end.y - start.y) * (pt.x - start.x) - (end.x - start.x) * (  
             pt.y - start.y);  
  };  
  const auto ra = region(b1, a1, a2) * region(b2, a1, a2) <= 0;  
  const auto rb = region(a1, b1, b2) * region(a2, b1, b2) <= 0;  
  
  if (ra && rb) {  
    const glm::vec2 v1 = a2 - a1;  
    const glm::vec2 v2 = b2 - b1;  
  
    // 2D scalar cross product  
    auto cross = [](const glm::vec2& u, const glm::vec2& v) {  
      return u.x * v.y - u.y * v.x;  
    };  
  
    const auto denom = cross(v1, v2);  
    if (std::fabs(denom) < eps) return std::nullopt;  
    // parallel / numeric guard  
  
    const auto t = cross(b1 - a1, v2) / denom;  
    return a1 + t * v1;  
  }  
  return std::nullopt;  
}

 ベジエ曲線の交差判定次はベジエ曲線と線分の交点を求めます。二次方程式の解の公式が使えるので、代入して直接交点のtを出してしまいましょう。P_iを制御点の座標としたとき、二次ベジエ曲線は以下の式で表されるのでした。

P(t) = (1-t)^2 P_1 + 2(1-t)t P_2 + t^2 P_3
ここで先程登場した直線のベクトル方程式について、x, yにベクトルを分解してtを消すと、

\begin{aligned}
Q(t)  &= Q_1 + (Q_2-Q_1)t \\
(x-x_1)(y_2 - y_1) &= (y-y_1)(x_2 - x_1)
\end{aligned}
このx,yにベジエ曲線の式を代入して、二次ベジエ曲線のtの二次方程式を解きます。以下のように係数ベクトルを用意するとすっきり表せます。
  
\begin{aligned}
L_1 &:= \text{直線の始点} \\
L_2 &:= \text{直線の終点} \\
L &= L_2 - L_1 \\
K &= \begin{bmatrix}
           L_{y} \\
           -L_{x}
         \end{bmatrix} \\
A &= P_1 - 2P_2 + P_3 \\
B &= 2(P_2 - P_1) \\
C &= P_1
\end{aligned}  
で、代入後の二次方程式は以下の通り。

\big(K \cdot A \big)t^{2}  
+\big(K \cdot B \big)t  
+\big(K \cdot (C - L_1)\big)=0
あとはこれを解いてtを出して、0 \leq t \leq1に含まれているかをチェックすればOKです。ちなみにちょくちょく登場しているepsは浮動小数点の誤差を許容するための小さな値です。
線分とベジエ曲線の交点を求めるコードGeometry.h
inline std::vector<glm::vec2> segmentQuadBezierIntersect(  
    const glm::vec2& p1, // bezier start  
    const glm::vec2& p2, // bezier control  
    const glm::vec2& p3, // bezier end  
    const glm::vec2& l1, // line start  
    const glm::vec2& l2 // line end  
    ) {  
  const auto k = glm::vec2((l2 - l1).y, -(l2 - l1).x);  
  const auto a = p3 - 2.0f * p2 + p1;  
  const auto b = 2.0f * (p2 - p1);  
  const auto c = p1;  
  
  const auto ts = solveQuadratic(  
      dot(k, a),  
      dot(k, b),  
      dot(k, c - l1)  
      );  
  
  std::vector<glm::vec2> intersects(0);  
  for (const auto t : ts) {  
    if (-eps <= t && t <= 1.0f + eps)  
      intersects.push_back(  
          a * t * t + b * t + c);  
  }  
  return intersects;  
}
ちなみに解析的に出す方法は解の公式がまともに使える二次ベジエ曲線までしか使えません。Bezier clippingという数値的に出す手法なら、より高次のベジエ曲線でも高速に判定できるようです。
http://nishitalab.org/user/nis/cdrom/cad/CAGD90Curve.pdf
交点を求める関数ができたので、塗りつぶしを実装していきます。
Even-odd法での塗りつぶしを行うコードvoid FrameBufferCanvas::renderGlyphByEvenOdd(const Glyph& glyph,  
                                             const RGB color,  
                                             const int startX) {  
  // Loop for each glyph components  
  for (const auto& c : glyph.getComponents()) {  
    const auto n = c.getNumOfVertices();  
    const auto coordinates = c.getCoordinates();  
    const auto endPtsOfContours = c.getEndPtsOfContours();  
    const auto ptsOnCurve = c.getPtsOnCurve();  
  
    transformMat[2][0] = startX;  
  
    // Cache of point vectors of vertices  
    std::unordered_map<int, glm::vec2> points;  
    for (int i = 0; i < n; ++i) {  
      // Convert coordinate system from bottom-up to top-down  
      points[i] = transformVec2(scale * transformMat, coordinates[i]);  
    }  
  
    // Loop for each scanline  
    auto rayStart = glm::vec2(0, 0);  
    auto rayEnd = glm::vec2(width, 0);  
    for (int y = 0; y < height; ++y) {  
      rayStart.y = rayEnd.y = static_cast<float>(y);  
      std::vector<int> intersections;  
      uint16_t contourStartPt = 0;  
      auto prevPt = glm::vec2(0.f);  
      // Loop for each vertex  
      for (int i = 0; i < n; ++i) {  
        const auto isEndPt = endPtsOfContours.contains(i);  
        const auto nextIdx = isEndPt ? contourStartPt : (i + 1) % n;  
        const auto isOnCurve = ptsOnCurve.contains(i);  
        const auto isNextOnCurve = ptsOnCurve.contains(nextIdx);  
        auto currentPt = points[i];  
        auto nextPt = points[nextIdx];  
  
        if (isOnCurve) {  
          if (isNextOnCurve) {  
            // on curve - on curve: Straight line  
            const auto s = segmentsIntersect(  
                currentPt, nextPt, rayStart, rayEnd);  
            if (s) {  
              intersections.emplace_back(static_cast<int>(s.value().x));  
            }  
          }  
          prevPt = currentPt;  
        } else {  
          // not on curve: Control point  
          if (!isNextOnCurve) {  
            // Calculate the implicit next "on-curve" from the middle point of next control point  
            nextPt = (currentPt + nextPt);  
            nextPt /= 2;  
          }  
          const auto ss = segmentQuadBezierIntersect(  
              prevPt,  
              currentPt,  
              nextPt,  
              rayStart,  
              rayEnd  
              );    
          for (const auto s : ss) {  
            intersections.emplace_back(static_cast<int>(s.x));  
          }  
          prevPt = nextPt;  
        }  
        if (isEndPt) contourStartPt = i + 1;  
      }  
  
      std::sort(intersections.begin(), intersections.end());  
      int cnt = 0;  
      int prevX = 0;  
      for (const auto x : intersections) {  
        if (cnt % 2 == 1) {  
          drawLine(prevX, y, x, y, 1, color);  
        }  
        cnt++;  
        prevX = x;  
      }  
    }  
  }  
}
おしい！ほぼほぼ塗りつぶされていますが、妙な線が現れています。2つの線分もしくは曲線が端点を共有するときにエラーが発生しているみたいです。詳しく見てみると、以下の2パターンで間違った塗りが起きていることがわかりました。同じ座標に交点があったとき、2つとも交点としてカウントしたい場合と無視したいケースがあるということです。
例えば以下画像の上のエラーでは、左からx座標421, 421, 679, 701, 823の5つの交点がカウントされており、421 - 421の線分が描写されたことでそれ以降が反転してしまっています。


カウントしすぎ
翻って、以下のパターンでは左からx座標394, 701, 823の3点のみカウントされていて、線分は394 - 701の間のみ描写されています。本来は左からx座標394, 701, 701, 823か394, 823のようにカウントされるべきです。


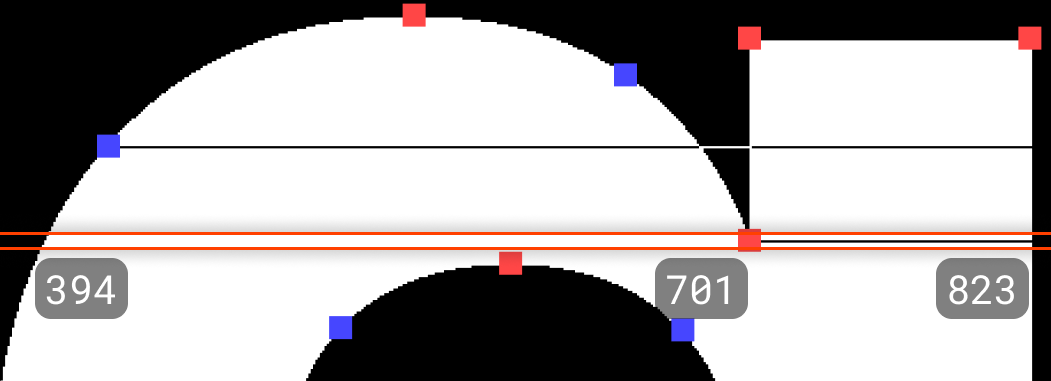
カウントたりない

 塗りつぶしエラーの除去これらのような一見一貫性のない挙動について、統一的に判定できる方法はあるでしょうか？まずは問題を単純にするために、どんなときにダブルカウントしてほしいか、もしくはしてほしくないかを、一旦まっすぐな線分で考察してみます。

2つの線分A,Bが端点を共有していて、スキャンラインがその座標を通るとき、A,Bのもう一方の端点について考えてみましょう。
スキャンラインより上か下どちらか一方にA,B両方の端点集まっている場合、ダブルカウントor無視
スキャンラインの上下にAとBの端点が別れているとき、一回のみカウントする　つまりどちらか片方を無視する

上下に分かれているときは２つの線分を一つの線分としてみなすイメージで、端点を共有していてもそこでダブルカウントされるべきではないということです。
線分の最小値がスキャンラインよりも小さいときのみ交点をカウントすると、上2つの条件をクリアできそうです。

厳密には、この方法では両端点がスキャンラインよりも下にある場合、1ピクセル分描写されなくなるため完璧な解法ではありませんが、エラーは除去されるため一旦この方法を採用します。
次に、曲線について考えてみましょう。基本的には直線と同じですが、以下のパターンを追加で考慮する必要があります。
曲線の端点がスキャンラインより下にあるが、曲線の一部が上にあるときはカウントする
曲線の端点がスキャンラインより上にあるが、曲線の一部が下にあるときは無視する
これのチェックを単純に行うには曲線の最小値を求められれば良さそうです。二次ベジエ曲線は先述の通り二次方程式で表せるので、極小時点のパラメータtを出して、tが曲線内に収まっていてかつ左上が原点の画像座標系で上に凸であるかどうかを確認します。

\begin{aligned}
y(t) &= (1-t)^2 y_{P_1} + 2(1-t)t y_{P_2} + t^2 y_{P_3} \\
y(t) &= (y_{P_1} - 2y_{P_2} + y_{P_3})t^2 + 2(y_{P_2} - y_{P_1})t + y_{P_1}
\end{aligned}
以下のようにおいて微分すると、

\begin{aligned}
a &= y_{P_1} - 2y_{P_2} + y_{P_3} \\
b &= 2(y_{P_2} - y_{P_1}) \\ 
c &= y_{P_1} \\
\\
y^\prime(t) &= 2at + b
\end{aligned}
このtをもとに先程の条件を確認すればOKです！
ベジエ曲線の最小値を求めるコードGeometry.h
inline int getBezierMinY(  
    const glm::vec2& p1, // bezier start  
    const glm::vec2& p2, // bezier control  
    const glm::vec2& p3 // bezier end  
    ) {  
  const auto a = p1.y - 2 * p2.y + p3.y;  
  const auto b = 2 * (p2.y - p1.y);  
  
  if (fabs(a) < eps) {  
    if (fabs(b) < eps) return static_cast<int>(p1.y);  
    return static_cast<int>(std::min(p1.y, p3.y));  
  }  
  // find the parameter when the curve reaches its extremum by taking the derivative  
  const auto t = -b / (2.0f * a);  
  // if the curve is convex upwards, the extremum can be the minimum y  
  if (-eps <= t && t <= 1.0f + eps && a > 0) {  
    return static_cast<int>(a * t * t + b * t + p1.y);  
  }  
  return static_cast<int>(std::min(p1.y, p3.y));  
}
最後に、上の画像の下に凸の場合を確認します。スキャンラインが曲線のどちらかの端点と同じy座標であり、スキャンラインと曲線が２つの交点を持ち、曲線が下に凸の場合、y座標がスキャンラインと同じ方の端点のカウントを無視すればOKです。これできれいに塗りつぶすことができました！
線分と線分の交点で発生するエラーを修正したコードFrameBufferCanvas.cpp
void FrameBufferCanvas::renderGlyphByEvenOdd(const Glyph& glyph,
                                             const RGB color,
                                             const int startX) {
  // Loop for each glyph components
  for (const auto& c : glyph.getComponents()) {
    const auto n = c.getNumOfVertices();
    const auto coordinates = c.getCoordinates();
    const auto endPtsOfContours = c.getEndPtsOfContours();
    const auto ptsOnCurve = c.getPtsOnCurve();

    transformMat[2][0] = startX;

    // Cache of point vectors of vertices
    std::unordered_map<int, glm::vec2> points;
    for (int i = 0; i < n; ++i) {
      // Convert coordinate system from bottom-up to top-down
      points[i] = transformVec2(scale * transformMat, coordinates[i]);
    }

    // Loop for each scanline
    auto rayStart = glm::vec2(0, 0);
    auto rayEnd = glm::vec2(width, 0);
    for (int y = 0; y < height; ++y) {
      rayStart.y = rayEnd.y = static_cast<float>(y);
      std::vector<int> intersections;
      uint16_t contourStartPt = 0;
      auto prevPt = glm::vec2(0.f);
      // Loop for each vertex
      for (int i = 0; i < n; ++i) {
        const auto isEndPt = endPtsOfContours.contains(i);
        const auto nextIdx = isEndPt ? contourStartPt : (i + 1) % n;
        const auto isOnCurve = ptsOnCurve.contains(i);
        const auto isNextOnCurve = ptsOnCurve.contains(nextIdx);
        auto currentPt = points[i];
        auto nextPt = points[nextIdx];

        if (isOnCurve) {
          if (isNextOnCurve) {
            // on curve - on curve: Straight line
            const auto s = segmentsIntersect(
                currentPt, nextPt, rayStart, rayEnd);
            const auto minY = static_cast<int>(std::min(currentPt.y, nextPt.y));
            if (s && minY < y) {
              intersections.emplace_back(static_cast<int>(s.value().x));
            }
          }
          prevPt = currentPt;
        } else {
          // not on curve: Control point
          if (!isNextOnCurve) {
            // Calculate the implicit next "on-curve" from the middle point of next control point
            nextPt = (currentPt + nextPt);
            nextPt /= 2;
          }
          const auto ss = segmentQuadBezierIntersect(
              prevPt,
              currentPt,
              nextPt,
              rayStart,
              rayEnd
              );
          const auto minY = getBezierMinY(prevPt, currentPt, nextPt);
          if (ss.size() == 2 &&
              !isBezierConvexUpwards(prevPt, currentPt, nextPt)) {
            if (y == static_cast<int>(prevPt.x) || y == static_cast<int>(nextPt.
                  x)) {
              if (static_cast<int>(ss[0].x) == static_cast<int>(prevPt.x)) {
                intersections.emplace_back(static_cast<int>(ss[1].x));
              } else {
                intersections.emplace_back(static_cast<int>(ss[0].x));
              }
            }
          } else if (minY < y) {
            for (const auto s : ss) {
              intersections.emplace_back(static_cast<int>(s.x));
            }
          }
          prevPt = nextPt;
        }
        if (isEndPt) contourStartPt = i + 1;
      }

      std::sort(intersections.begin(), intersections.end());
      int cnt = 0;
      int prevX = 0;
      for (const auto x : intersections) {
        if (cnt % 2 == 1) {
          drawLine(prevX, y, x, y, 1, color);
        }
        cnt++;
        prevX = x;
      }
    }
  }
}

 Non-zero法Even-odd法はシンプルなアルゴリズムな一方、以下のように輪郭が重なっているときに穴が空いてしまいます。
これを改善する方法のひとつに、Non-zero法があります。Non-zero法は基本的にEven-odd法と同じでスキャンラインを使って輪郭と交差する点を見ていきますが、交差回数の偶奇ではなく、スキャンラインが跨いだ輪郭をなす線の向きが上向きなら+1、下向きなら-1としてカウントしていき、0より大きいときに塗ることで穴を発生させずに塗りつぶせる、というアルゴリズムです。グリフの輪郭をなす頂点は右回りもしくは左回りに並んでいるのでそれを利用します。ちなみにブラウザでのsvgのデフォルトの塗りつぶしにはnon-zero法が用いられています。
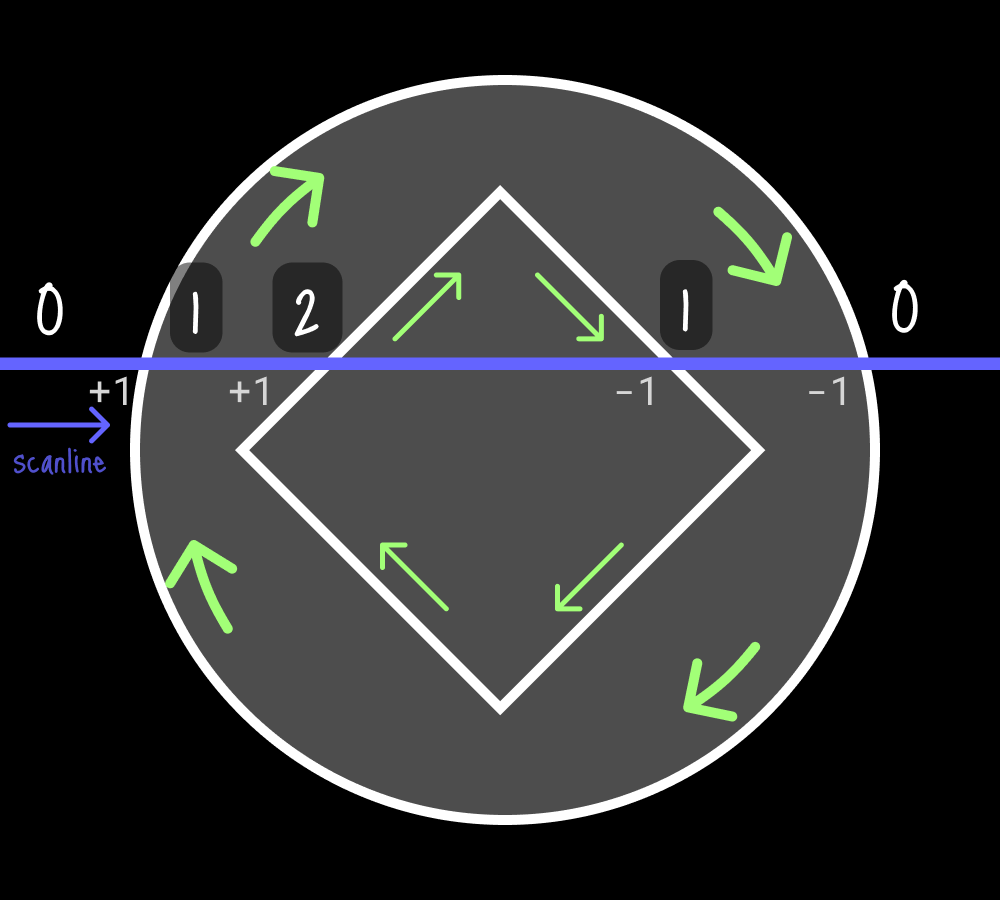
一旦線分だけ考慮して実装してみましょう。Even-oddの交差回数カウントの代わりに以下の処理に入れ替えます。

currentPt.y > nextPt.yのとき、isUpwardを交差点に付与する

isUpwardが0より大きい区間だけ塗りつぶす
線の向きを考慮したレンダリングのコードFrameBufferCanvas.cpp
...
if (isOnCurve) {  
  if (isNextOnCurve) {  
    // on curve - on curve: Straight line  
    const auto s = segmentsIntersect(  
        currentPt, nextPt, rayStart, rayEnd);  
    const auto minY = static_cast<int>(std::min(currentPt.y, nextPt.y));  
    if (s && minY < y) {  
      intersections.emplace_back(  
          static_cast<int>(s.value().x),  
          currentPt.y > nextPt.y);  
    }  
  }  
  prevPt = currentPt;  
}
...
int prevCount = 0;  
int prevX = 0;  
int count = 0;  
for (const auto& [x, isUpward] : intersections) {  
  isUpward ? ++count : --count;  
  if (prevCount > 0 && count >= 0) {  
    drawLine(prevX, y, x, y, 1, WHITE);  
  }  
  prevCount = count;  
  prevX = x;  
}
直線だけで構成されているグリフで比較すると、ばっちり塗りつぶせています！


Even-odd法では穴ぼこだったグリフが


綺麗に塗りつぶされた
曲線があっても実はほぼほぼ問題なく塗れていますが、以下のように一部うまく行かないケースがあります。
右下のエラー箇所の線分は{x: 713, isUpwards: true}, {x: 902, isUpwards: false}としてintersectionsに追加されていて問題ありませんし、線分の端点上で発生しているわけではなさそうです。よーく見ると右下のエラー箇所と同じy座標の左下にもエラーがあって、実はここが原因でした。ちょっと分かりづらいですが、左下の本当はもう少しだけ上にカーブが続くはずの部分が描写されていないことがわかります。
ここでの問題はスキャンラインと曲線で交点が2つある場合の線の向きの判定です。曲線の端点のy座標どうしを比較しても2つの交点がそれぞれどちら向きかがわからないため、正しくカウントされずエラーになっていたのでした。このケースでは、以下の図のようにカウントすればうまくレンダリングできそうです。


スキャンラインと曲線が2つの交点を持つ場合の2パターン
この図を眺めてみると、曲線が上下どちらに凸かと、線分のスタートの場所の2要素で判定できることが分かります。
上に凸のとき、線分のスタートに近い側の交点は上向き、もう一方は下向き
下に凸のとき、線分のスタートに近い側の交点は下向き、もう一方は上向き
思いの外簡単なチェックで曲線の問題をカバー出来ました！
ベジエ曲線がスキャンラインと2つの交点を持つ場合を修正したコードFrameBufferCanvas.cpp
rvoid FrameBufferCanvas::renderGlyphByNonZero(const Glyph& glyph,  
                                             const RGB color,  
                                             const int startX) {  
  // Loop for each glyph components  
  for (const auto& c : glyph.getComponents()) {  
    const auto n = c.getNumOfVertices();  
    const auto coordinates = c.getCoordinates();  
    const auto endPtsOfContours = c.getEndPtsOfContours();  
    const auto ptsOnCurve = c.getPtsOnCurve();  
    const auto rect = c.getBoundingRect();  
  
    transformMat[2][0] = startX;  
  
    // Cache of point vectors of vertices  
    std::unordered_map<int, glm::vec2> points;  
    for (int i = 0; i < n; ++i) {  
      // Convert coordinate system from bottom-up to top-down  
      points[i] = transformVec2(scale * transformMat, coordinates[i]);  
    }  
    auto rayStart = glm::vec2(0, 0);  
    auto rayEnd = glm::vec2(width, 0);  
  
    // Transform the coordinate of the bounding rect  
    const auto top = transformVec2(  
        scale * transformMat, glm::vec2(0, rect.yMax)).y;  
    const auto bottom = transformVec2(  
        scale * transformMat, glm::vec2(0, rect.yMin)).y;  
    for (int y = top; y < bottom; ++y) {  
      rayStart.y = rayEnd.y = static_cast<float>(y);  
      std::vector<Intersection> intersections;  
      uint16_t contourStartPt = 0;  
      auto prevPt = glm::vec2{0, 0};  
      // Loop for each vertex  
      for (int i = 0; i < n; ++i) {  
        const auto isEndPt = endPtsOfContours.contains(i);  
        const auto nextIdx = isEndPt ? contourStartPt : (i + 1) % n;  
        const auto isOnCurve = ptsOnCurve.contains(i);  
        const auto isNextOnCurve = ptsOnCurve.contains(nextIdx);  
        auto currentPt = points[i];  
        auto nextPt = points[nextIdx];  
  
        if (isOnCurve) {  
          if (isNextOnCurve) {  
            // on curve - on curve: Straight line  
            const auto s = segmentsIntersect(  
                currentPt, nextPt, rayStart, rayEnd);  
            const auto minY = static_cast<int>(std::min(currentPt.y, nextPt.y));  
            if (s && minY < y) {  
              intersections.emplace_back(  
                  static_cast<int>(s.value().x),  
                  currentPt.y > nextPt.y);  
            }  
          }  
          prevPt = currentPt;  
        } else {  
          // not on curve: Control point  
          if (!isNextOnCurve) {  
            // Calculate the implicit next "on-curve" from the middle point of next control point  
            nextPt = (currentPt + nextPt);  
            nextPt /= 2;  
          }  
          // bezier line  
          const auto ss = segmentQuadBezierIntersect(  
              prevPt,  
              currentPt,  
              nextPt,  
              rayStart,  
              rayEnd  
              );  
  
          const auto minY = getBezierMinY(prevPt, currentPt, nextPt);
          if (minY < y) {  
            if (ss.size() == 1) {  
              intersections.emplace_back(static_cast<int>(ss[0].x),  
                                         prevPt.y > nextPt.y);  
            } else if (ss.size() == 2) {  
              auto nearestX = [&](const glm::vec2& pt) -> int {  
                return static_cast<int>((std::fabs(pt.x - ss[0].x) <  
                                         std::fabs(pt.x - ss[1].x))  
                                          ? ss[0].x  
                                          : ss[1].x);  
              };  
              const int closeXtoCur = nearestX(prevPt);  
              const int closeXtoNxt = nearestX(nextPt);  
              const auto convexUpwards = isBezierConvexUpwards(  
                  prevPt, currentPt, nextPt);  
              intersections.emplace_back(closeXtoCur, convexUpwards);  
              intersections.emplace_back(closeXtoNxt, !convexUpwards);  
            }  
          }  
          prevPt = nextPt;  
        }  
        if (isEndPt) contourStartPt = i + 1;  
      }  
  
      std::sort(intersections.begin(), intersections.end(),  
                [](const Intersection& a, const Intersection& b) {  
                  return a.x < b.x;  
                });  
      int prevCount = 0;  
      int prevX = 0;  
      int count = 0;  
      for (const auto& [x, isUpward] : intersections) {  
        isUpward ? ++count : --count;  
        if (prevCount > 0 && count >= 0) {  
          drawLine(prevX, y, x, y, 1, color);  
        }  
        prevCount = count;  
        prevX = x;  
      }  
    }  
  }  
}


文句なし！
これで自作のTrueTypeパーサーとレンダラーで任意の文字列を表示できるようになりました。お疲れ様でした！！

 おわりにまずは長大な記事を最後まで読んで頂きありがとうございました！バイトを一つずつ読み込み、1ピクセルの描写から始めることで、普段意識しないフォントや2Dレンダリングの世界で何が起こっているのか大筋を理解することが出来たと思います。
この記事で作ったパーサーやレンダラーは本当に最低限の機能しかなく、TrueTypeにはまだまだ面白いトピックが詰まっています。例えばヒンティングは、低解像度環境でのリーダビリティを改善するためにグリフ位置を微調整するための技術です。他にもカーニング、合字、縦書きもありますね。アンチエイリアスも大きなトピックです。今回のレンダリングではパフォーマンスを考慮しませんでしたが、GPUを使ったレンダリングの並列化や、GPUに最適化したスキャンラインとは全く異なるアルゴリズムもあります。これらに興味を持たれたら、ぜひとも自分で作って理解してみてください！

 参考文献Fonts - TrueType Reference Manual - Apple Developer

TrueType fundamentals (OpenType 1.9.1) - Typography | Microsoft Learn

Tutorial — FontForge 20230101 documentation

TrueType - Wikipedia

フォント TrueType 構造解析 - yonewiki

Software rendering in 500 lines of bare C++ - Playing with code

ベジェ曲線入門

線形補間 - Wikipedia

nishitalab.org/user/nis/cdrom/cad/CAGD90Curve.pdf

Even–odd rule - Wikipedia

Nonzero-rule - Wikipedia
型	説明
shortFrac	16-bit 符号付き小数
Fixed	16.16-bit 符号付き固定小数点数
FWord	16-bit 符号付き整数 (単位: FUnit)
uFWord	16-bit 符号なし整数 (単位: FUnit)
F2Dot14	16-bit 符号付き固定小数点数上位2ビットが整数部、下位14ビットが小数部
longDateTime	64-bit 1904年1月1日12:00からの秒数
型	名前	説明
uint32	scaler type	OSX, iOS用のスケール
uint16	numTables	テーブルの数
uint16	searchRange	(maximum power of 2 <= numTables)*16
uint16	entrySelector	log2(maximum power of 2 <= numTables)
uint16	rangeShift	numTables*16-searchRange
型	名前	説明
uint32	tag	テーブル名 (例: glyf)
uint32	checkSum	テーブルのチェックサム
uint32	offset	ファイル先頭からテーブル先頭へのオフセット(バイト)
uint32	length	テーブルサイズ(バイト)
型	名前	説明
UInt16	version	バージョン番号(現在は0固定)
UInt16	numberSubtables	サブテーブルの数
型	名前	説明
UInt16	platformID	プラットフォーム識別子
UInt16	platformSpecificID	プラットフォーム特有のID
UInt32	offset	マッピングテーブルへのオフセット
型	名前	説明
UInt16	format	サブテーブルフォーマット(12固定)
UInt16	reserved	予約済みエリア(0固定)
UInt32	length	ヘッダ含むこのサブテーブルのバイト長
UInt32	language	言語コード
UInt32	nGroups	グルーピングの数
型	名前	説明
UInt32	startCharCode	グループ最初のUnicode
UInt32	endCharCode	グループ最後のUnicode
UInt32	startGlyphCode	最初のGlyphCode 以降の文字は連続したGlyphCodeが割り当てられる
型	名前	説明
longHorMetric	hMetrics[numOfLongHorMetrics]	グリフのMetric
FWord	leftSideBearing[]	Here the advanceWidth is assumed to be the same as the advanceWidth for the last entry above. The number of entries in this array is derived from the total number of glyphs minus numOfLongHorMetrics. This generally is used with a run of monospaced glyphs (e.g. Kanji fonts or Courier fonts). Only one run is allowed and it must be at the end.
型	名前	説明
int16	numberOfContours	輪郭の数プラスならSimple glyph マイナスならCompound glyph
FWord	xMin	x座標最小値
FWord	yMin	y座標最小値
FWord	xMax	x座標最大値
FWord	yMax	y座標最大値
型	名前	説明
uint16	endPtsOfContours[n]	輪郭の最後の点のインデックスの配列(n=輪郭数)
uint16	instructionLength	インストラクションの長さ
uint8	instructions[instructionLength]	インストラクション
uint8	flags[variable]	フラグの配列(n=頂点数)
uint8 or int16	xCoordinates[]	x座標(n=頂点数)
uint8 or int16	yCoordinates[]	y座標(n=頂点数)
フラグ	ビット	説明
On Curve	0	オン: 曲線の上オフ: 曲線の外
x-Short Vector	1	オン: x座標が1バイトオフ: x座標が2バイト
y-Short Vector	2	オン: y座標が1バイトオフ: y座標が2バイト
Repeat	3	オン: 次の1バイトに入っている数だけ同じフラグが続くオフ: リピートしない
This x is same (Positive x-Short vector)	4	オン: 2がオンならx座標がプラス、2がオフなら一つ前のx座標と同じオフ: 2がオンならx座標がマイナス、2がオフならx座標は次のuint16
This y is same (Positive y-Short vector)	5	オン: 2がオンならx座標がプラス、2がオフなら一つ前のy座標と同じオフ: 2がオンなら6座標がマイナス、2がオフならy座標は次のuint16
Reserved	6 - 7	使用されていない
WE_HAVE _A_SCALE	WE_HAVE AN_X_AND Y SCALE	WE_HAVE_A TWO_BY TWO	a	b	c	d
0	0	0	1.0	0.0	0.0	1.0
1	0	0	1st short	0.0	0.0	1st short
0	1	0	1st short	0.0	0.0	2nd short
0	0	1	1st short	2nd short	3rd short	4th short
型	名前	説明
uint16	flags	フラグ
uint16	glyphIndex	読み込み先のGlyphCode
int16, uint16, int8 or uint8	argument1	変数1 フラグによって内容が変わる
int16, uint16, int8 or uint8	argument2	変数2 フラグによって内容が変わる
transformation option		変形オプション
フラグ	ビット	説明
ARG_1_AND_2_ARE_WORDS	0	オン: 変数1の型がWord オフ: Byte
ARGS_ARE_XY_VALUES	1	オン: 変数はx,y座標オフ: アンカーポイント
ROUND_XY_TO_GRID	2	ビット1がオンのときだけ読むオン: x,yをグリッドに合わせて丸めるオフ: 丸めない
WE_HAVE_A_SCALE	3	オン: 後に与えられる値でスケールするオフ: スケール値を1とする
(this bit is obsolete)	4	使われていないフラグ
MORE_COMPONENTS	5	オン: この次にまだComponentがあるオフ: もうない
WE_HAVE_AN_X_AND_Y_SCALE	6	オン: x座標のスケールがy座標と異なるオフ: x,yどちらも同じスケーリング
WE_HAVE_A_TWO_BY_TWO	7	オン: 線形変換用の2x2行列が与えられるオフ: 与えられない
WE_HAVE_INSTRUCTIONS	8	オン: インストラクションがあるオフ: ない
USE_MY_METRICS	9	オン: このComponentのmetricをCompound glyphのmetricとするオフ: しない
OVERLAP_COMPOUND	10	オン: このCompound glyphはcomponentsがオーバーラップしてできているオフ: オーバーラップがない
目的

TrueTypeとは

超ざっくりTrueTypeの仕組み

TrueTypeパーサー グリフデータの取得準備

ttfファイル読み込み

オフセットテーブル

cmapテーブル

locaテーブル

hhea, hmtxテーブル

レンダラーの準備

グリフのパース & アウトラインの描写

glyfテーブルのパース

Simple glyph

アウトラインを直線でレンダリング

Compound glyph

レンダラー 曲線の描写

ベジエ曲線の定義

ド・カステリョのアルゴリズム

TrueTypeのベジエ曲線

レンダラー グリフの塗りつぶし

Even-odd法

線分の交点

ベジエ曲線の交差判定

塗りつぶしエラーの除去

Non-zero法

おわりに

参考文献

Discussion

TrueTypeパーサー　グリフデータの取得準備

レンダラー　曲線の描写

レンダラー　グリフの塗りつぶし
