🌒

Android, Chromeを支える2Dレンダリングエンジン　Skiaのコードを読んで気持ちを理解する

に公開
C++
低レイヤ
ベジェ曲線
2D
skia
tech

Skiaという2Dグラフィックスライブラリの名前を耳にしたことがありますか？もし聞いたことがなくても、Skiaを使ったアプリケーションやOSには絶対触れたことがあるはずです。それほどにも普遍的に使われているにも関わらず、Skiaのアーキテクチャや実装に触れた情報が意外にも少なく、謎のヴェールに包まれているような印象を受けることでしょう。ここではそんなSkiaのソースコードを読んで得たCPU実装の全体像とコア部分の実装の詳細について共有します。Skia、ひいては2Dレンダリングエンジンが図形を描く時、一体何が行われているのか見当がつくようになれば幸いです。

この記事の目的

SkiaのCPU実装について、特にパスがレンダリングされるまでの理解を深めることが主な目的です。GPU実装については触れません。ユーザー向けAPIの紹介と、CPUバックエンドアーキテクチャの概要解説でSkiaの全体像を掴んだ後、レンダリングの要であるラスタライズパイプラインとパスの描画対象ピクセル判定についてより詳しく見ていきます。特にパスの描画判定は膝を打つようなアルゴリズムと実装がたくさん出てきますので、後半までぜひ！目を通していただけると嬉しいです。

Skiaとは

Skiaは現在Googleが開発しているC++で書かれたオープンソースの2Dグラフィックスライブラリです。多様なバックエンドを持ち、Android, Chrome OS, Chrome, Firefox, Flutterなどさまざまなレイヤーにてグラフィックスエンジンとしての役割を果たしています。
ビットマップデータも対応しますが、特筆すべきはベクターグラフィックスのラスタライズができることです。難しく聞こえるかもしれませんが、以下のような任意の形状を描いてピクセルデータとして吐き出せるということです。似たソフトウェアにはCairo、Quartz 2D、Direct2D、Pathfinderなどが挙げられます。


Documentation | Skiaより引用

ユーザー向けAPI

まずユーザー向けAPIから見ていきましょう。以下が主なクラスの例で、とてもシンプルで直感的なAPIが提供されています。

  • SkSurface: 描画する対象のサーフェス
  • SkImage: イミュータブルなピクセルデータ（画像など）
  • SkPath: パスデータを保持するオブジェクト
  • SkFont: タイプフェイスやテキストスタイルを保持するオブジェクト
  • SkPaint: スタイル情報を保持するオブジェクト　色、スタイル、ブレンド、マスクなど
  • SkCanvas: 描画用インターフェイスを持つオブジェクト drawPath, drawImageなど

そのほかのAPIはこちらから確認できます。
https://api.skia.org/

使い方については具体例を見るのが手っ取り早いです。基本的にはSurfaceを作ってCanvasを取得し、PathとPaintオブジェクトを作ってからCanvasに描画するという流れです。Skia Fiddleというプレイグラウンドが用意されているので、実際に触ってみると理解が早まると思います。
https://fiddle.skia.org/c/939b541feb37a8f29ef51e2d949df511

以下の例ではSkia Fiddleを使っているのでSurfaceとCanvasは作成済みです。

void draw(SkCanvas* canvas) {
    canvas->clear(SK_ColorBLACK);

    SkPaint p;
    p.setAntiAlias(false);
    p.setBlendMode(SkBlendMode::kPlus);
    const SkColor4f midGray = {0.5f, 0.5f, 0.5f, 1};
    auto srcCS = SkColorSpace::MakeSRGB();
    p.setColor4f(midGray, srcCS.get());

    SkPathBuilder b1;
    b1.moveTo(15.3f, 15.3f);
    b1.lineTo(40.8f, 239.7f);
    b1.cubicTo(96.9f, 214.2f,
               168.3f, 204.0f,
               239.7f, 204.0f);
    b1.cubicTo(188.7f, 117.3f,
               112.2f, 40.8f,
               15.3f, 15.3f);
    b1.close();
    SkPath path1 = b1.detach();

    SkPathBuilder b2;
    b2.moveTo(239.7f, 15.3f);
    b2.lineTo(214.2f, 239.7f);
    b2.cubicTo(158.1f, 214.2f,
               86.7f, 204.0f,
               15.3f, 204.0f);
    b2.cubicTo(66.3f, 117.3f,
               142.8f, 40.8f,
               239.7f, 15.3f);
    b2.close();
    SkPath path2 = b2.detach();

    canvas->drawPath(path1, p);
    canvas->drawPath(path2, p);
}

CPUバックエンドアーキテクチャ

SkiaのCPUバックエンドのアーキテクチャについて、2025年8月末に公式ドキュメントが追加され、全体像を把握しやすくなりました。
https://skia.googlesource.com/skia/+/6887dcf153bf/docs/architecture/CPU.dot

以下は公式ドキュメント添付の概要図です。
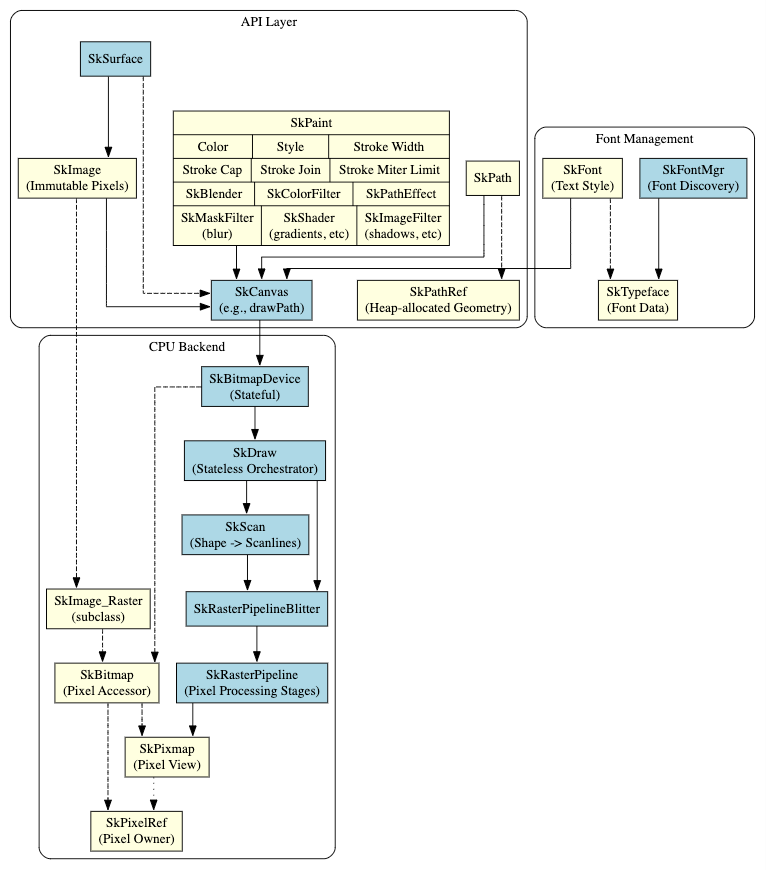
Skia CPUバックエンドアーキテクチャの概要図

SkiaのバックエンドはCPU、GPUの両方に対応しています。今回はピクセルレベルでの描画を追うため、CPUバックエンドに絞って見ていきます。（私はまだ読めていませんが、恐らくGPUバックエンドの実装はかなり異なるものと思われます。）
CPUバックエンドは主に以下のオブジェクトによって構成されます。Path, Paint等で作成されるベクターシェイプのことをこれ以降シェイプと呼ぶことにします。

  • skDraw: 一つのシェイプに対して一つ生成されるステートレスなオーケストレータです。パス形状やスタイリングシェイプ、変形などの描画に必要な手続きをまとめる役割を担います。
  • skScan: ラスタライザの中心部で、シェイプをスキャンラインごとの塗るべきX区間に変換します。高さ1pxの水平スパンにシェイプを分割するイメージです。ここでは色とエフェクトには関与しません。アンチエイリアスがオンの場合、coverage maskをピクセルにジオメトリがどれぐらい被っているか計算し、滑らかになるようアルファを足します。
  • skRasterPipelineBlitter: Scanで分割した矩形のレンダリングを行うオブジェクトです。後述のパイプラインを実行し、その結果をPixmapなどに書き出します。
  • skRasterPipeline: ラスタライズのステージを管理するオブジェクトです。色塗り、ブレンドやマスクなどのステージを数珠繋ぎにしたパイプラインを作成し、Blitterからの描画命令に対してパイプラインが実行され、最終的に出力されるピクセルの色を計算します。
  • skPixmap: ピクセルが書き出される宛先です。

ここまでは公式ドキュメントで紹介されている内容でした。ここから一歩踏み込んで、CPUバックエンドで重要な役割を果たすラスタライズパイプラインとパスの描画対象ピクセル判定（スキャン）について実装を覗いてみましょう！

SkRasterPipeline - ラスタライズパイプライン

ラスタライズに必要な処理やその順番はアンチエイリアスの有無、マスクかどうか、ブレンドモードなどによって変わります。Skiaではこれらの処理をできるだけ同じインターフェイスで実行できるように、ピクセル情報が必要な各処理を1ステージと置いたパイプラインとして実装されています。
ラスタライズパイプラインはSkRasterPipelineに実装されています。具体的には以下のような機能を持っています。

  • パイプラインは複数のステージからなる
  • パイプラインはグローバルコンテクストを持ち、ステージ間で共有する
  • ステージは一つのピクセルに対して実行される関数
  • すべてのステージは高精度実装を持つ
  • いくつかのステージは低精度実装を持つ
  • 各ステージの実行が終わるとき、次のステージを呼び出す
  • パイプラインのコンパイル時、すべてのステージが低精度実装を持つ場合、低精度パイプラインが用いられる　それ以外の場合、高精度パイプラインが用いられる
  • パイプラインのコンパイルは関数へのポインタのリストを作る

ここがパフォーマンスのキモなので、各ステージの実装では条件分岐やループが極力使われていません。ステージの演算はひとつのピクセルに対して行われ、また各ピクセルの演算結果は他のピクセルの結果に影響しないため、並列計算が可能になります。例えば、多くのステージではSIMDで演算を並列化しています。高精度ステージ実装のSkRasterPipeline_opts.hのfloor関数を見てみると、各CPUアーキテクチャに合わせたSIMD用処理が行われているのがわかります。

https://github.com/google/skia/blob/a32353e15e57ff5e96fa7a9f3725be2aaaa6dec9/src/opts/SkRasterPipeline_opts.h#L5619-L5646

それではパイプラインが実際に生成されているコードの具体例を見ていきましょう。SkRasterPipelineBlitter::blitRectです。Blitterのなかでおそらく一番シンプルな、矩形を描画するためのメソッドです。この中でfColorPipelineが土台として登場しますが、これはSkRasterPipelineBlitter::Createで作られています。

https://github.com/google/skia/blob/2467a35eeba8b255c7ac7fc546a5b957f4624d07/src/core/SkRasterPipelineBlitter.cpp#L301-L498

https://github.com/google/skia/blob/2467a35eeba8b255c7ac7fc546a5b957f4624d07/src/core/SkRasterPipelineBlitter.cpp#L530-L567

ここでは以下のステージたちが上から順番にパイプラインに詰められています。

  • Clip用Shader: クリップ領域のアルファを生成
  • Shader: ソースの塗りに使う色の生成（一色、グラデーション、画像だったり）
  • ColorFilter: Shaderに当たるフィルタ
  • LoadDst: 宛先ピクセルの読み込み
  • Blend: ソースと宛先を合成
  • ClipLerp: クリップアルファで補完
  • Store: 宛先へ結果を書き込む

端折った最適化パスやステージがありますが大体こんな感じです。パイプライン周りのコードは巨大で複雑ですが、こうして見てみると思いの外シンプルな処理体系ということが分かると思います。大事なのは、行う処理によってこれらのステージの順番が内容が変わっても、Blitterから見たパイプライン作成->描画というインターフェイスは同じということです。

SkScan - 描画対象ピクセルの判定

ここからが本丸！パスの描画対象ピクセルの判定です。パスの描画は指定したエリア内のピクセルに対して、パイプラインを実行することで完了します。このピクセルの内外判定について高速かつシンプルに行うため、Skiaでは鮮やかなアルゴリズムが用いられています。

一般的にベクターシェイプの塗りつぶしに使われているアルゴリズムとして、Even-odd法とNon-zero法が挙げられます。これらはどちらも任意の直線を引いたときにベクターの輪郭と交差した回数を元に塗りつぶしエリアを判定する方法です。この任意の直線はスキャンラインと呼ばれ、多くの場合X軸に並行な直線のY座標を1pxずつ移動させスキャンする手法が取られます。つまり、あるY座標において、パスの輪郭のX座標がどこにあるか？という問題を判定すれば良いということです。

evenodd法とnonzero法の例
左:Even-odd法　右:Non-zero法

https://oreillymedia.github.io/Using_SVG/extras/ch06-fill-rule.html

このセクションではまず線分のみで構成されたパスがどのようにスキャンされるのかを追い、その後に二次ベジェ曲線がどのように処理されるのかを見ていきます。

直線のスキャン

まず、線分とスキャンラインとの交点を求めるとき、ナイーブな方法では以下のステップを踏むことになります。

  • 線分の端点がスキャンラインの上下に分かれているか確認
  • スキャンラインのY座標を、線分をなす直線の式に代入してxを求める

具体的には以下のような式になります。

\begin{aligned} y - y_1 &= \frac{y_2 - y_1}{x_2 - x_1}(x - x_1) \\ x &= \frac{x_2 - x_1}{y_2 - y_1}(y - y_1) + x_1 \end{aligned}

ここでの問題点は、この計算をスキャン対象のpx高さ\times線分の個数だけ行う必要があるということです。スキャンラインを用いたラスタライズの場合、計算回数自体は省略しづらいので仕方ないのですが、スキャンごとに割り算と掛け算が発生するのはどうにかしたいですね。

前進差分での計算効率化

Skiaでは、先ほどの問題を前進差分を用いることで高速化しています。ラスタライズはピクセルの集まりという離散的な出力へと変換する作業です。そしてスキャンラインはスキャン対象の高さ分、1pxずつ上から順に動かしてパスの輪郭との交差判定を行います。ということは、パスを構成するそれぞれの辺（エッジ）について、Y座標が1px動いたときにX座標はどれだけ変化するか(=dx)、つまり前進差分を事前に計算しておくことができます。これにより、スキャン時にはエッジの現在のX座標に変化量dxを足していくだけで、スキャンラインとの交点を高速に求めることができるのです！

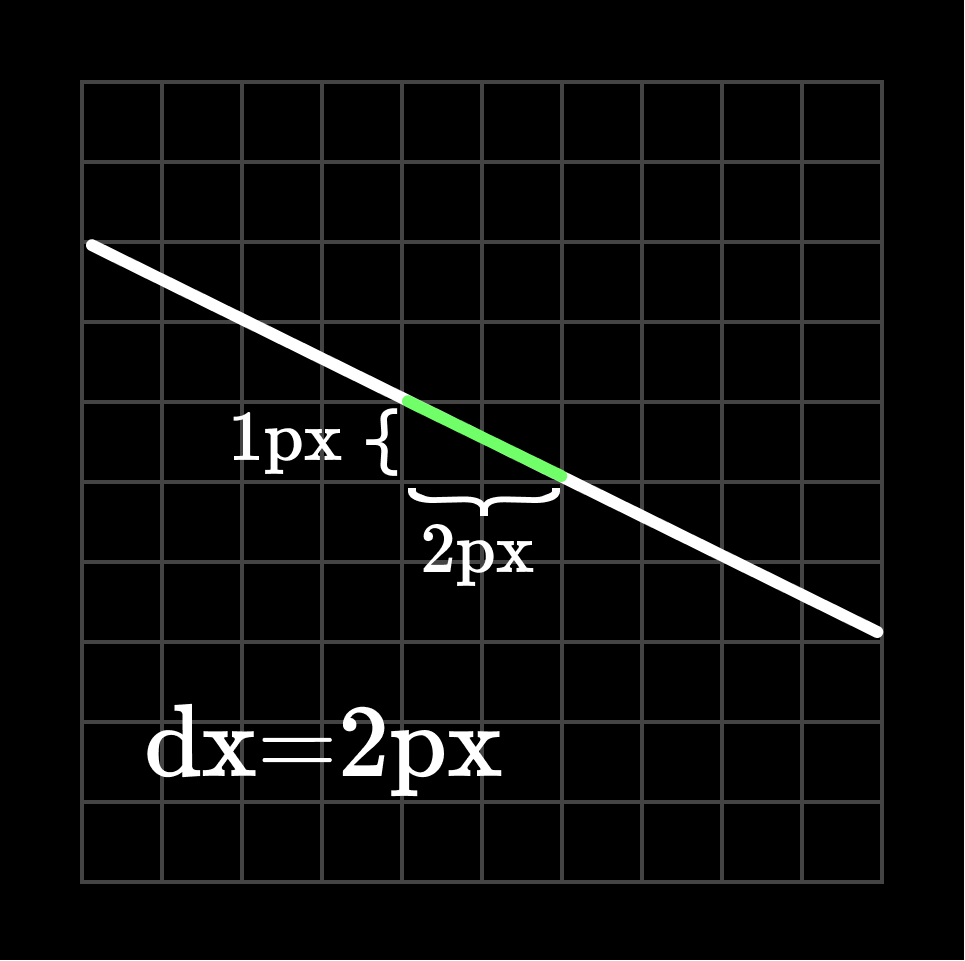
前進差分の例

それでは実装を見てきましょう。ここでは、パスがどのように前進差分を持ったエッジに変換されるか、そしてどのようにスキャンされるかに注目して追っていきます。

ユーザー向けAPIのSkPath::lineToが実行されるとSkPathVerb::kLineというEnumと点情報がPathに保存されます。そのパスを描画するCanvasのメソッドのSkCanvas::drawPathはskcpu::Draw::drawPathにパスを渡し、途中で作成されたblitterと共にskScanに辿り着きます。（途中でSkPathRawに変換されていますが基本的には不要な情報を落としたSkPathです。）そしてsk_fill_pathがパスからエッジを作成+スキャンを実行する役割を担います。

https://github.com/google/skia/blob/f5e0ae7c1b4a0cbcfaf9fa3abe09e815ea82097f/src/core/SkScan_Path.cpp#L392-L465

まずはエッジ作成の実装であるSkBasicEdgeBuilder::buildEdgesを覗いてみましょう。

SkBasicEdgeBuilder::buildEdges

ここではSkPathRawにまずクリッピング処理を行い、SkBasicEdgeBuilder::build -> SkBasicEdgeBuilder::addLine->SkEdge::setLineと呼び出し、skEdgeオブジェクトに変換されます。実装を見てもらうと分かる通り、現在地のfXに加えて、前進差分であるfDxDyが作られています！他には線分のY座標情報でfFirstY, fLastY、Non-zero法で用いるためのパスの方向情報であるfWindingもEdgeのフィールドに保存されます。

https://github.com/google/skia/blob/f5e0ae7c1b4a0cbcfaf9fa3abe09e815ea82097f/src/core/SkEdge.cpp#L99-L150

パスのクリッピングも面白い処理が行われていますが、ここではエッジへの変換とスキャンによる描画に集中するため、記事最後の補足箇所で紹介します。

walk_edges

ここで先ほど前進差分を求めたエッジを用いラスタライズが行われます。ここでは全てのエッジに対してスキャンラインとの交点を確認する必要があるため、二重ループになっています。ループの中では現在のエッジとスキャンラインとの交点であるfXを用い、Even-odd法かNon-zero法かに応じてスパンを計算し、BlitterのblitHで1px\timesスパン幅の矩形を描画します。そしてループの最後にエッジのfXをnewX = currE->fX + currE->fDxDyのようにして更新することで、次のループ開始時点では、fXがすでにスキャンラインとエッジの交点のX座標になっているというわけです。
この通り、前進差分を使うことによって毎回除算を含む重たい交点計算をする必要がなくなり、効率的なレンダリングに寄与していることが分かったと思います！

https://github.com/google/skia/blob/f5e0ae7c1b4a0cbcfaf9fa3abe09e815ea82097f/src/core/SkScan_Path.cpp#L115-L200

二次ベジェ曲線のスキャン

続いて二次ベジェ曲線の処理を見ていきましょう！そもそもベジェ曲線とは、以下の式で表される曲線なのでした。

B(t) = \sum_{i=0}^{n} \binom{n}{i} (1 - t)^{n - i} t^i P_i, \quad 0 \le t \le 1

ここでは二次ベジェ曲線を見ていくので以下の式になりますね。

B(t) = (1-t)^2 P_0 + 2(1-t)t P_1 + t^2 P_2

そのままの曲線ではスキャンラインと高々2回交差するため、場合分けがしんどく、前進差分が使いづらいという問題があります。これをSkiaでは以下の方法で解決しています。

モノトニックなベジェ曲線への分割

曲線とスキャンラインが2回交差する可能性がある問題について、そもそも曲線をモノトニック（単調増加 or 単調減少）になるように分解するという解決策がとられています。二次ベジェ曲線は二次関数のため、極値が最大一つしかありません。つまり極値で二つの曲線に分割することで、それら二つはモノトニックであることが保証されます。

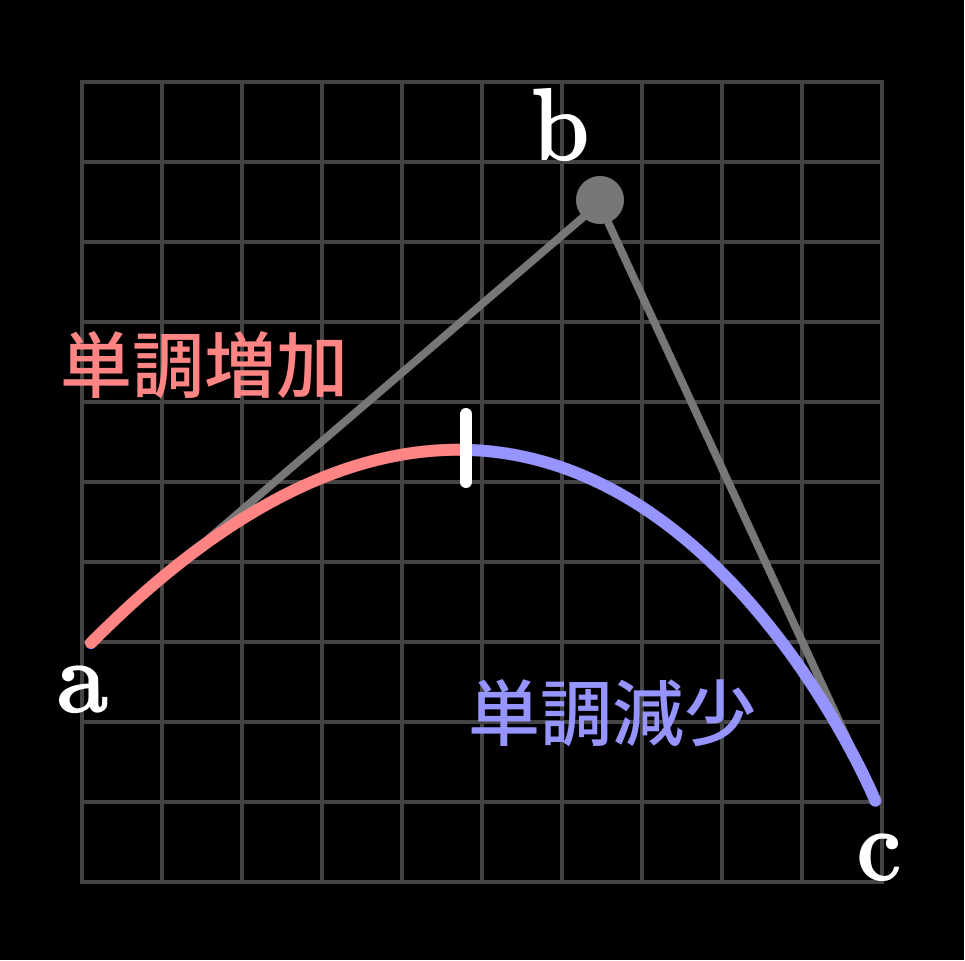
モノトニックに分割された二次ベジェ曲線
二次ベジェ曲線は極値で分割すると単調増加 or 単調減少になる

ここで実装を見てみましょう。skGeometory.cppのSkChopQuadAtYExtremaでY座標の極値で二次ベジェ曲線を分割しています。

https://github.com/google/skia/blob/1db567519d52ebfa579beefcbff3984f80fe307b/src/core/SkGeometry.cpp#L276-L302

ここで面白いのが、"曲線がモノトニックかどうか"の判定です。以下のis_not_monotonicの実装は一見簡単ですが、これでなぜ判定ができるのでしょうか？

https://github.com/google/skia/blob/1db567519d52ebfa579beefcbff3984f80fe307b/src/core/SkGeometry.cpp#L43-L50

制御点をa, b, cと置いたとき、二次ベジェ曲線は以下の式で表されます。ここでパラメータのtは0から1の間である必要があります。（ここで0\leq t \leq 1 でないのはSkiaの実装に合わせてです）

% 二次ベジェの y 成分 \begin{aligned} B(t) &= (1-t)^2 a + 2(1-t)t\, b + t^2 c, \quad t \in (0,1) \\ \end{aligned}

まずこの曲線の導関数を求めてみます。

\begin{aligned} B'(t) &= 2(b-a) + 2(a-2b+c)t \end{aligned}

このtはベジェ曲線の傾きが0になる箇所のパラメータですね。つまり、このtが0<t<1の範囲に入っていれば、極値がベジェ曲線の中にあるということです。なのでひとまずtについて解いてみましょう。

\begin{aligned} % 極値（内点）条件：y'(t)=0 の解 t &= \frac{a-b}{a-2b+c}\\ \end{aligned}

ここで簡単のためにu = a-b, v = b - cとおき、不等式を解きます。

\begin{aligned} 0 &<\frac{u}{u-v}<1 \\ \\ \end{aligned}

0より大きい条件を見ます。uとu-vは正負が揃っている必要があるため以下が成り立ちます。

0 < \frac{u}{(u-v)} \quad \rightarrow \quad 0 < u(u-v)

1より小さい条件をみます。すると、

\frac{u}{(u-v)} < 1 \quad \rightarrow \quad \begin{cases} u-v>0\text{のとき,}\quad 0 > v \\ u-v<0\text{のとき,}\quad 0 < v \end{cases}

よって最終的に

\begin{cases} u-v \neq 0 \\ u-v>0\text{のとき,}\quad 0 > v \text{かつ} 0 < u\\ u-v<0\text{のとき,}\quad 0 < v \text{かつ} 0 > u \end{cases}

が成り立ちます。つまり、a-bとb-cが異符号であれば、この曲線は極値を持つことになります。先ほどの小さな実装はこのような変形がなされた効率的なチェックだったということですね。

ベジェ曲線は分割しても同じ次数のベジェ曲線になりますので、分割処理後にSkEdgeBuilder::addQuadにてモノトニックになった曲線をエッジとして追加しています。

二次ベジェ曲線を複数の線分で近似（Curve flattening）

続けてスキャンラインとの交差判定を見ていきます。二次ベジェ曲線も線分同様に一階微分と二階微分の結果を持ったエッジとすることで前進差分で今のX座標がわかります。理論的には曲線は曲線として扱うこともできるはずですが、Skiaでは曲線を線分で近似して、直線と同じ実装でスキャンを行なっています。これは恐らく計算精度の担保と実装の単純化のためだと思われます。この曲線を線分で近似することをCurve flatteningと呼び、ここでもとても面白い工夫がなされています！実装はSkQuadraticEdge::setQuadratic周辺で行われています。

https://github.com/google/skia/blob/da137b1f13d8e372df60c4ee2f44ca151ab6f6ed/src/core/SkEdge.cpp#L251-L366

ここで求めたい最も重要な情報が、"直線で曲線を十分滑らかに近似できる分割回数"です。まずは「曲線を直線で近似」とはどういう状態かを考えています。二次ベジェ曲線は3つの制御点を持ち、最初と最後の制御点が曲線の端点になります。ここで、その二つの端点を直線で結んだ線分を考えてみましょう。すると以下のように、曲線と線分の間に隙間ができますよね。この隙間の最大をEと置いたとき、Eが指定した許容誤差内に収まっていれば「曲線を直線で近似」できた状態になったと言えます。（以下の図では分割の見やすさを重視して、モノトニック化していない曲線を使った例にしています）

曲線と直線の差
曲線と直線の差

さてこのEはどこで最大になるでしょうか。二次ベジェ曲線が制御点a,b,cからなるとき、B(t)が曲線の式、L(t)が二つの端点a,cを結ぶ直線の式とおきます。

\begin{aligned} B(t) &= (1-t)^2 a + 2(1-t)t\, b + t^2 c \\ L(t) &= (1-t)a + tc \end{aligned}

ここでE(t) = \|B(t) - L(t)\|とおくと、

\begin{aligned} E(t) &= \|\{(1-t)^2 - (1-t)\}a + 2(1-t)tb - t(1-t)c\| \\ &= \|-t(1-t)(a - 2b + c)\| \end{aligned}

のように変形できます。これによってt=\frac{1}{2}のところで最大になることがわかりました。従って、以下の式で誤差Eの最大値を求めることができます。

\begin{aligned} E(\frac{1}{2}) &= \frac{1}{4}\|(2b - a - c)\| \end{aligned}

実装ではsetQuadraticの以下の部分にてこの計算が行われています。

// compute number of steps needed (2^shift) based on the distance between  
// this curve at the half-way point (t=0.5) and the midpoint of a straight  
// line between p0 and p2.  
// B(1/2) = p0 (1-t)^2 + 2 p1 t(1-t) + p2 t^2; t = 1/2  
//        = p0 (1/2)^2 + 2 p1 (1/2)(1/2) + p2 (1/2)^2  
//        = 1/4 (p0 + 2 p1 + p2)  
// Midpoint of p0 and p2 is M(p0, p2) = (p2 + p0) / 2  
// Subtracting the two terms to get the vector representing the difference  
// distance = B(1/2) - M(p0, p2)  
//          = 1/4 (p0 + 2 p1 + p2) - (p2 + p0) / 2  
//          = 1/4 (p0 + 2 p1 + p2) - (2 p2 + 2 p0) / 4  
//          = 1/4 (-p0 + 2 p1 - p2)  
SkFDot6 deltaX = (2*x1 - x0 - x2) >> 2;  
SkFDot6 deltaY = (2*y1 - y0 - y2) >> 2;

この誤差Eは分割前の最大誤差なので、E_0と置きます。このE_0を用いて、E_n < \text{許容誤差} Fとなるnを探します。
ここで曲線をt=\frac{1}{2}の位置で分割したとき、制御点a側は[a, \frac{a+b}{2}, \frac{a+2b+c}{4}]の制御点をもつ二次ベジェ曲線になります。このaの誤差E_1を計算すると以下のようになります。

\begin{aligned} E_1 &= \frac{1}{4}\|(a - 2\frac{a+b}{2} + \frac{a + 2b + c}{4})\| \\ E_1 &= \frac{1}{16}\|a - 2b + c\| \\ E_1 &= \frac{E_0}{4} \end{aligned}

これで曲線をt=\frac{1}{2}で分割していくと、誤差E_nは(\frac{1}{4})^nで小さくなっていくということが分かりました！図を見てもらうとより直感的に理解できると思います。

Curve flattening　1段階目
Curve flattening 1段階目

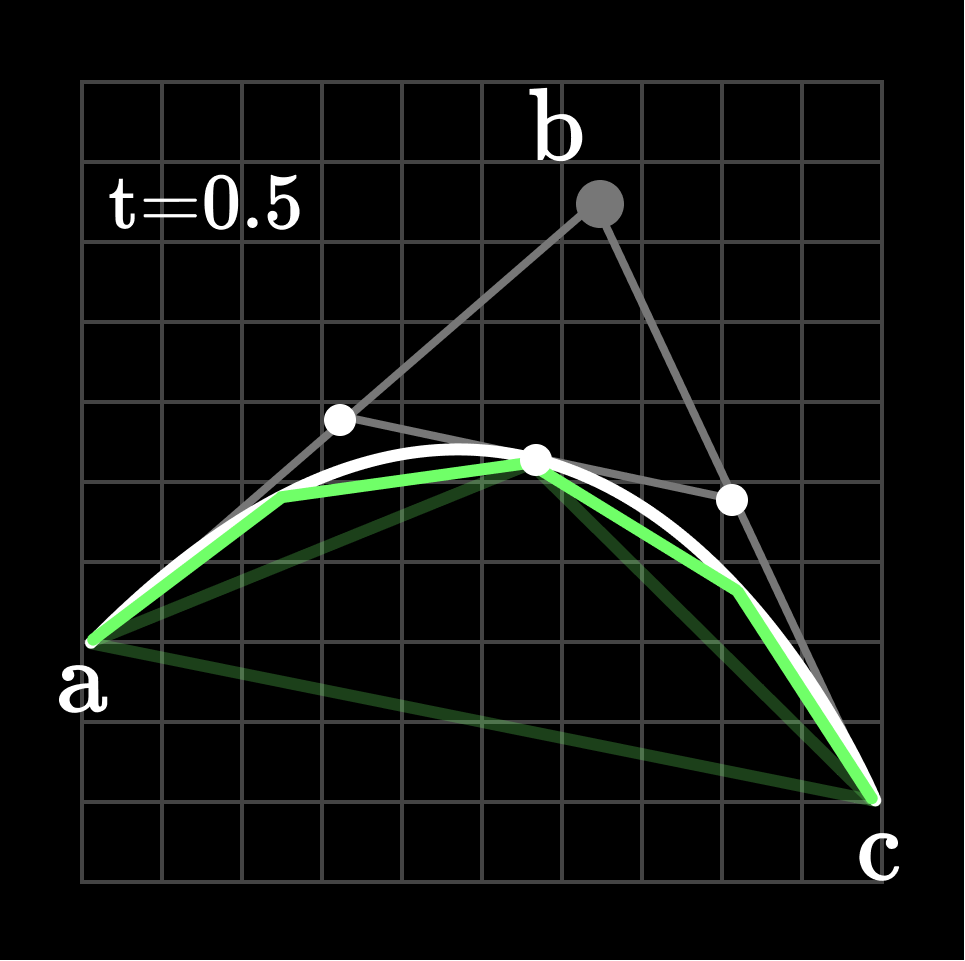
Curve flattening　2段階目
Curve flattening 2段階目

よって許容誤差Fを用いて、n=\lceil \log_4{\frac{E_0}{F}} \rceil を求めれば良いということになります。これは以下のように実装されています。Skiaではこの許容誤差Fを1/8pxと設定しています。

https://github.com/google/skia/blob/da137b1f13d8e372df60c4ee2f44ca151ab6f6ed/src/core/SkEdge.cpp#L234-L249

エッジ関係の計算にはビットシフトが多分に使われているため、若干読むのが難しいです。setQuadraticから呼び出される時accuracyは0なので、単純化すると

dist = (dist + 4) >> 3
dist = round(dist >> 3)

ということになります。（コードの最初のdist = 上記のE_0を近似した値です）ここでSkiaでは計算誤差を管理するためFDot6という固定小数点型を使っています。つまり整数部を取り出すには右に6回シフトする必要があります。そしてそれを許容誤差1/8で割る、つまり左に3回シフトすることで\frac{E_0}{F}が求まるので、以上のような計算になっているのです。
最後に(32 - SkCLZ(dist)) >> 1ですが、これはdistのビット長を求めてから1/2しています。ビット長はそのまま\log_2{\text{dist}}の整数部になり、\log_{4}{\text{dist}}への底の変換で1/2しているということです。これで近似するための分割回数を手に入れることができました！

最後に、 fQDxDt, fQD2xDt2に分割回数を考慮したパラメータ t 方向の前進差分用の一階・二階の差分係数持っておき、これらを使ってスキャン時に必要に応じて近似した線分を取り出します。線分を取り出してしまえば、あとは線分のラスタライズと同じ処理で描画できるというわけです！

https://github.com/google/skia/blob/640d2ba451888dcf65553781b095e7650b0d30de/src/core/SkEdge.cpp#L368-L403

補足

パイプラインとパスの塗りつぶしのほかに、個人的に面白いと感じたトピックにここで少し触れます。

tiny-skia

Skiaのサブセットとして、Rustで実装されたtiny-skiaというプロジェクトがあります。Skiaの実装はあまりに巨大でビルドにも時間がかかるという理由で開発された、名前のとおり小さいSkiaです。フォントレンダリングや解析的AA、GPUレンダリングなど実装されていない機能は多いですが、その分コードサイズはずっと小さく、CPUレンダリング部分はかなりSkiaの実装に近いので、使う側にも実装する側にも易しい作りになっています。私もSkiaを読む足掛かりとしてtiny-skiaのコードリーディングから始めました。Skiaの実装に興味を持たれた方は、まずこちらから覗いてみるのが良いかもしれません。

https://github.com/linebender/tiny-skia

クリッピング

パスの塗りつぶしで少し触れましたが、ラスタライズではクリッピングも大事な要素の一つです。例えば画面などのクリップ枠からはみ出た部分のレンダリングは行っても意味がないため、塗りの実行前にクリッピングを行います。Skiaではエッジに対して、X軸方向にはみ出た分をクリップ枠の左右に沿わせるようなイメージで、縦線に変形するアプローチをとっています。これはNon-zero法などのアルゴリズムで交差や巻き数カウントに関連したバグを起こさないためです。これに関しては以下の図を見てもらったほうが理解しやすいと思います。

クリッピング前のパス
クリップからはみ出したパスは

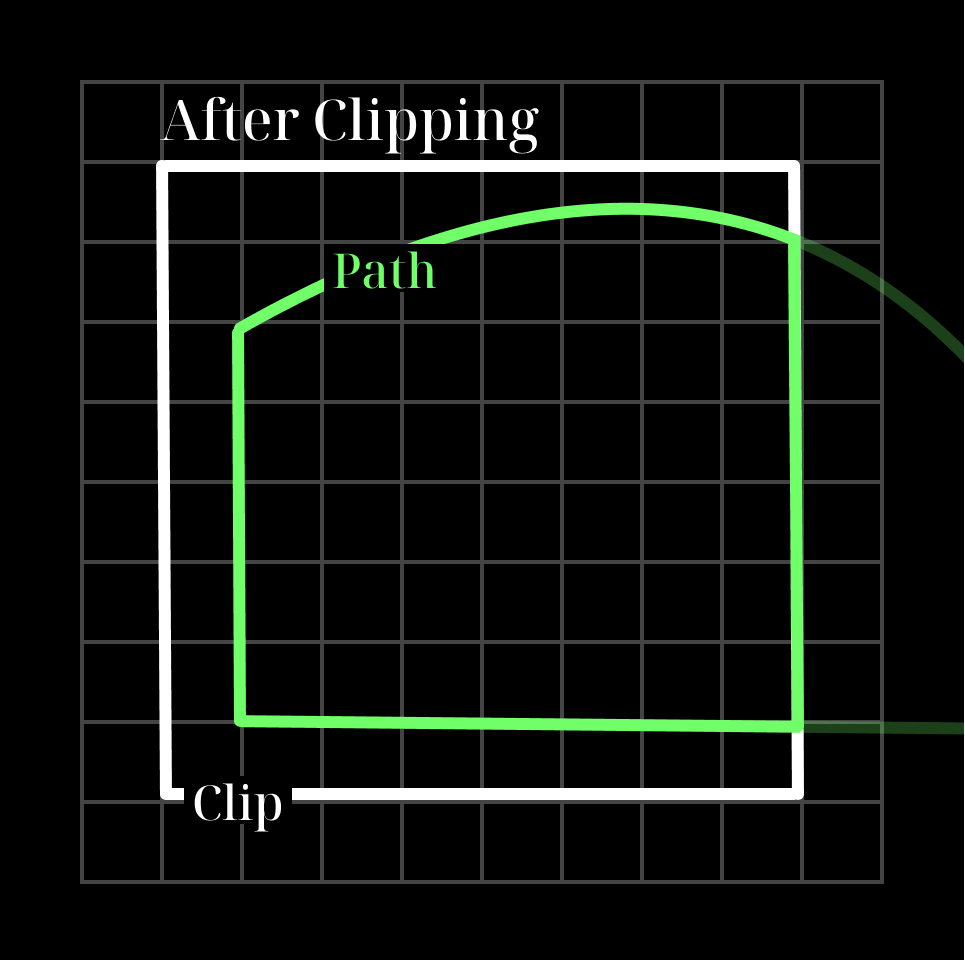
クリッピング後のパス
こうなる

色空間

Skiaでは、色のブレンドは最終出力されるサーフェスの色空間上で行われます。つまり宛先がsRGB色空間なら、128を二つ加算ブレンドすると255にクリップされるということです。一度リニアな色空間に変換しない理由として、昔は色空間をリニアに変換せずブレンドすることが多くあったため、その結果を想定した実装のアプリケーションを壊さないためとのことです。リニアワークフローを望むユーザーは最初からリニア色空間を持つSurfaceを作成してからレンダリングし、その結果をSkiaの外でsRGBにエンコードすれば良いということですね。以下のドキュメントに詳しい説明があります。
https://skia.org/docs/dev/design/raster_tragedy/

ちなみに、tiny-skiaでは一旦リニア色空間に変換してからブレンドを行うため、同じ命令を渡しても異なる結果になります。しばらくなぜなのか分からず詰まったところなのでした。


左がSkia、右がtiny-skiaのRGB128加算ブレンド結果

アンチエイリアス

SkiaのCPUラスタライズでアンチエイリアスをオンにすると、スーパーサンプリングではなく解析的AA（AAA = Analytic Anti-Alias）を用います。AA用のスキャンを固定幅ではなくエッジの高さ分進めて、一つ前のスキャンラインと今のスキャンラインが作る台形の面積を算出し、その台形の左右の辺にかかるピクセルのカバレッジを計算するような流れみたいですが、あまりちゃんと理解できませんでした…　公式ドキュメントがあるので、興味がある方はぜひ覗いてみてください。
https://skia.org/docs/dev/design/aaa/

おわりに

最後まで読んでいただきありがとうございました！一見簡単そうなベクターグラフィックスのラスタライズについて、こんなに面白い工夫の上に高性能レンダリングが成り立っているのだと実感してもらえたなら嬉しいです。
実世界ではGPUを使ったレンダリングが行われることがほとんどだと思いますが、ソフトウェアラスタライザはピクセル単位での描写まで追えるので、コードリーディングをするのに丁度良い題材だと思います。Skiaは大きなライブラリで多分自分が追えたのは多分全体の10％も無いぐらいだと思うので、興味を持たれた方はぜひご自身でも覗いてみてはいかがでしょうか。

参考文献

https://api.skia.org/
https://skia.googlesource.com/skia/%2B/6887dcf153bf/docs/architecture/CPU.md
https://www.slideshare.net/slideshow/introduction-to-skia/40799000
https://www.chromium.org/developers/design-documents/graphics-and-skia/
https://oreillymedia.github.io/Using_SVG/guide/blend-modes.html
https://agg.sourceforge.net/antigrain.com/research/adaptive_bezier/
https://docs.google.com/document/d/17Gq-huAf9q7wA4MRfXwpi_bYLrVeteKcSfAep0Am-wA/edit?tab=t.0
https://www.youtube.com/watch?v=K2QHdgAKP-s

Discussion