競プロ解説 [ABC345D]

はじめに

本記事は、日々の精進で出会った問題の一部を丁寧目に解説することで、筆者と読者のアルゴリズム力を向上させることを目的としています。

問題

方針（全探索）

タイルを左上から順番に敷き詰めていくことを考えます。タイルを並べる順番の選び方は $N!$ 通りあります。タイルの向きの組み合わせは $2^N$ 通りです。すべての順番と向きについて左上からタイルを敷き詰めていくことでこの問題を解くことができます。

タイルを $2$ 次元配列で管理する

タイルを管理するデータ構造として一番初めに思いつくのは $H \times W$ の $2$ 次元配列でしょうか？　これは正しい方法ですが、問題があります。それを明らかにするために、上で述べた方針を疑似コードとして表現してみます。

for タイルを設置する順番 { // O(N!)
    for タイルを設置する向き {  // O(2^N)
        'next_tile: for 順番と向きが指定されたタイルたち {
            for (i, j) in まだタイルが置かれていないマス {       // O(HW)
                if タイルの左上が (i, j) になるように配置できる { // O(HW)
                    タイルを配置する //O(HW)
                    continue 'next_tile;
                }
            }
        }
        if 全てのマスにタイルが設置されている { //O(HW)
            println!("Yes");
            return;
        }
    }
}
println!("No");

タイルを設置する回数が高々 $N$ 回であることに注意すると計算量は $O\big(HW (N + HW) 2^N N! \big)$ です。本問題の制約では $HW (N + HW) 2^N N!\sim 6 \times 10^9$ で
TLE してしまいます。

以上の考察からわかるように、$2$ 次元配列でタイルを管理する場合、タイルの設置判定に $O(HW)$ の計算が必要です。次節で紹介するビット列を用いる方法では、これを $O(HW/A)$ で実現できます^[1]。とくに本問題では $O(1)$ です。この場合の計算量は $O(NHW2^NN!)$ で十分高速です。

（時間）計算量はプログラムを実行するのに必要な時間を大雑把に比較する手段です。実行時間が $N$ に比例して増大するとき「計算量が $O(N)$」と表現します。これは複数のプログラムを実行時間で評価する上で有用です。

$N \sim 10^8$ のとき、実行時間がおよそ $1$ 秒であることが知られています。

計算量について詳しく知りたい方は次のページを参考にしてください。
https://qiita.com/drken/items/872ebc3a2b5caaa4a0d0

タイルをビット列で管理する

各マスの状態はタイルの有無の $2$ 通りだけです。$1$ マスの状態を $1$ ビットに対応づけることができるので、マスの状態は長さ $HW$ のビット列で表現できます。タイルも同様です。本問題の制約では $HW \le 100$ なので、u128 で十分です。

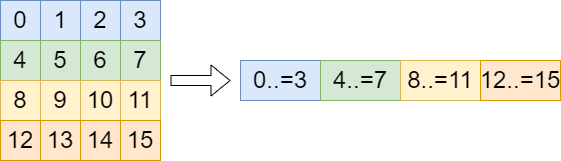
さらに、ビット演算を活用して以下の操作を $O(1)$ で実現できます。

操作	ビット演算
タイルを $1$ マス移動させる	tile <<= 1
タイルを設置できるか調べる	tile & grid == 0
タイルをマスに設置する	grid |= tile

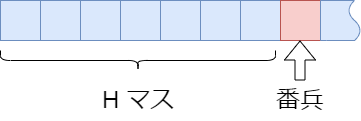
番兵法で折り返しをチェックする

タイルの移動にビットシフトを利用すると、マス目の右端でタイルが折り返してしまうことがあります。これをチェックするために、マス目の右端に $1$ ビット使うことを考えます。このビットに $1$ が立っているとき、タイルが不正な状態にあることが分かります。同様にして、ビットシフトの終了も判定できます。このような手法を番兵法と言います。

番兵法とは配列などのデータ構造にダミーの要素を追加し、それにより何らかの判定を行う手法を指します。本問題では、ビット列に対して番兵法を利用します。

回答例

use itertools::Itertools;
use proconio::input;

fn main() {
    input! { n: usize, h: u8, w: u8, ab: [(u8, u8); n], }
    let (h, w) = (h.min(w), h.max(w));

    // 同じ操作をクロージャでまとめる。
    let convert_to_bit =
        |a: u8, b: u8| (0..a).fold(0u128, |acc, i| acc + (((1 << b) - 1) << i * (w + 1)));

    let filled = convert_to_bit(h, w);
    let overflowed = u128::MAX - (1 << h * (w + 1) - 1) + 1;
    let sentinel = u128::MAX - overflowed - filled;
    let (tile_h, tile_v): (Vec<_>, Vec<_>) = ab
        .into_iter()
        .map(|(a, b)| (convert_to_bit(a, b), convert_to_bit(b, a)))
        .unzip();

    // 使用するタイルの組を指定して高速化
    for i in 1..=n {
        for set in (0..n).combinations(i) {
            // タイルのサイズの合計がマス目のサイズと一致しない場合はダメ。「枝刈り」という。
            if set.iter().fold(0, |acc, &i| acc + tile_h[i].count_ones()) as u8 != h * w {
                continue;
            }

            for order in set.iter().copied().permutations(i) {
                for rotated in 0..1 << i {
                    let mut grid = 0;

                    // 向きと順番が指定されたタイルを設置していく
                    'next_tile: for mut tile in (0..i).map(|i| match rotated & 1 << i {
                        0 => tile_h[order[i]],
                        _ => tile_v[order[i]],
                    }) {
                        tile <<= (sentinel & grid).trailing_ones();
                        while tile & overflowed == 0 {
                            if tile & (sentinel | grid) == 0 {
                                grid |= tile;
                                continue 'next_tile;
                            }
                            tile <<= 1;
                        }
                        // 設置できないタイルがあるとダメ。ここで、for rotated ...
                        // にジャンプすると、次の if 文が不要
                        break;
                    }

                    if grid == filled {
                        println!("Yes");
                        return;
                    }
                }
            }
        }
    }

    println!("No")
}

脚注

1. たとえば、ビット列が Vec<u64> で実装されているとき $A = 64$ です。bitset_fixedクレートを参照してください。