技術負債とプロダクト成長の関係に関する数理モデルの考察〜改善フェーズ移行を見据えた定量的な理解
TL;DR
- プロダクトの成長は、初期のスピードと長期の減衰のバランスで決まる
- 技術的負債や開発プロセスの歪みは、長期の減衰(=成長の鈍化)として表れる
- ロジスティック成長モデルに減衰項を加えることで、成長と改善フェーズ(=新規開発ではなく、技術的負債の解消・再設計に向けたフェーズ)の切り替えを数値的に捉えられる
- ペアプロ・生成AI・コーディングルールなどは、長期の減衰を抑えるための手段として有効
- 「PoC後に丁寧に作る」ではなく、初期からペアプロ・生成AI・コーディングルールなどを取り入れたハイブリッド戦略が重要
- プロダクト価値の成長とARRなどの成果指標をつなげることで、経営判断にも活かせる
1. 導入
1.1 なぜ今、数理モデルで考えるのか
プロダクト開発において、「技術負債」と「スピード」のトレードオフに悩むことは少なくありません。初期のスピードを優先すればするほど、将来的な保守性や拡張性のコストが重くのしかかってくる——こうした状況を、もう少し定量的に理解できないか?という問いから、このモデルは始まっています。
今回用いるのは、ロジスティック成長モデル[1]に減衰項を加えた拡張モデルです。以下のような式で、プロダクトの成長を捉えます:
ここで各パラメータは以下のように定義されます:
-
R(t) t -
K -
A -
r -
\alpha
このモデルを用いることで、「プロダクトがいつ改善フェーズに入るべきか?」を、感覚ではなく数値的な変化として観測できるようになります。
1.2 なぜロジスティック成長モデルか
ロジスティック成長モデルは以下の数式で表され、次のような曲線を描きます。

ロジスティック成長曲線には以下のような利点があります:
-
S字カーブで現実の成長パターンを再現できる
初期は緩やか→急激に拡大→やがて飽和。この典型パターンは多くのプロダクト成長に共通します。 -
限界(キャパシティ)を明示的に持つ
K -
改善フェーズの兆候を数値として捉えられる
成長が鈍化し始める転換点(成長率の一次導関数の変化)を観察できます。
さらに、今回は時間とともに成長が自然に鈍化する現象を捉えるため、減衰項
2. 二つの開発アプローチの対比
このセクションでは、プロダクト開発における2つの典型的なスタイルをモデルに当てはめて比較してみます。
- アプローチA:雑に速く作る
- アプローチB:最初にしっかり作る
どちらが良い悪いというよりも、それぞれの選択が成長モデルのどのパラメータにどう影響を与えるのか?という観点で整理します。
2.1 アプローチA:雑に速く作る
-
初期成長率
r
とにかく速くリリースするため、初期の立ち上がりは非常にスムーズ。 -
減衰率
α
技術負債が溜まりやすく、数ヶ月後には改善・保守のコストが増大。 -
結果として、短期的には爆発的に伸びるが、中長期では失速する
グラフで言えば、成長曲線は急激に立ち上がった後、早期にピークアウトしてしまいます。
このケースでは、以下のような状態が起こりやすいです:
- 要件が曖昧なまま実装が進む
- テストやドキュメントが後回しになる
- 実装者依存のコードが増える
- 後からのリファクタに大きな労力がかかる
2.2 アプローチB:最初にしっかり作る
-
初期成長率
r
設計や合意形成、テスト整備などに時間をかけるため、初期のアウトプット量は抑えめ。 -
減衰率
α
設計品質やプロセス整備によって、長期的には安定した成長が見込まれる。 -
結果として、最初は地味でも継続的にスケーラブルな成長ができる
離脱の少ないユーザー基盤や、変更に強いコードベースが築かれやすくなります。
このようなプロセスでは:
- ドメインに即した設計がなされる
- CI/CDや自動テストが整備される
- ペアプロやレビューが品質を担保する
- 属人性が排除され、誰でも保守しやすい状態が保たれる
2.3 図式で捉える:r \alpha
| スタイル | 初期成長率 |
減衰率 |
コメント |
|---|---|---|---|
| 雑に速く | 高い | 高い | 初期は爆速、早期に限界 |
| 丁寧に構築 | やや低い | 低い | 緩やかに伸びて持続性が高い |
このパラメータの組み合わせが、プロダクトの将来の形を決定づけます。
次のセクションでは、実際にこのモデルを用いてパラメータを設定し、どのような成長曲線が描かれるのかをシミュレーションしてみます。
3. 数理モデルへの落とし込み
前セクションで示した2つの開発スタイルを、実際に数式モデルに落とし込んでいきます。
このセクションでは、ロジスティック成長モデルに減衰項を組み合わせた以下の数式をベースに、各パラメータがどのような意味を持つのかを具体的に説明します:
3.1 パラメータ設計
それぞれのパラメータは、プロダクト開発や組織運営の観点から以下のように置き換えられます。
K
- プロダクトが最終的に到達しうる限界値
- 市場規模、経営リソース、戦略的な到達目標を反映
- 例:潜在ユーザー数、営業リソースの上限、チームの対応力など
r
- プロダクトの立ち上がりスピード
- スプリントあたりのリリース量、仕様の明確さ、要件定義の精度などを反映
- 自動化や生成AIの活用度にも影響される
A
- 初期に発生する開発上の摩擦、足並みの乱れを表す
- 方向性の不明確さ、合意形成の不十分さ、外部との調整コストなどが該当
- 小さいほどスムーズに成長を始められる
\alpha
- 時間の経過とともに、どれだけ成長が鈍化するかを定量化
- 技術的負債やプロセスの乱れが影響
- モデルの中でも最も重要なパラメータの一つ
3.2 減衰率 \alpha
具体的にどのようなメトリクスが影響するのかを、以下に整理します:
| 技術的メトリクス | 状態が悪化すると( |
状態が良化すると( |
|---|---|---|
| 変更容易性(Change Lead Time) | 改修や新機能のリードタイムが長くなり、改善が遅延する | 顧客要望に素早く対応でき、価値提供の速度が維持される |
| バグ再発率 | 品質問題で手戻りが頻発し、成長の勢いが削がれる | 修正が安定し、新規開発に集中できる |
| PRの滞留時間 | コード変更の反映が遅れ、開発スループットが低下する | 開発リズムが保たれ、成長スピードが維持される |
| モジュール化率 | 再利用しづらく、変更に毎回コストがかかる | 拡張が容易になり、継続的改善が実現しやすい |
| 属人性の高さ(知識が特定の人に集中) | 離職・変更時の引き継ぎが困難になり、対応スピードが低下 | ナレッジが共有され、誰でも継続的な改善ができる |
これらのメトリクスをモニタリングすることで、
3.3 成長スコア R(t)
このモデルにおける
たとえば以下のように解釈できます:
これをビジネス指標に変換すると:
つまり、
4. シミュレーション(モデルを動かしてみる)
これまで説明してきた拡張ロジスティック成長モデルを使って、実際に成長曲線をシミュレーションしてみます。
4.1 シミュレーション条件とパラメータ設定
以下の2つの開発アプローチについて、それぞれパラメータを設定しました:
| パラメータ | 雑に速く作る | 丁寧に構築する | 現実的な意味づけ |
|---|---|---|---|
| 100 | 100 | 最終的な成長の上限(市場キャパシティ)を同一に設定 | |
| 2.0 | 4.0 | 雑に作る方が障壁が小さく、立ち上がりが早い | |
| 0.6 | 0.3 | 雑に作る方が初速は高く、丁寧な構築はスロースタート | |
| 0.08 | 0.02 | 雑に作る方が技術的負債が蓄積しやすく、減衰が大きい |
この設定は、たとえば以下のような現場を想定しています:
- 雑に速く作るチーム:初期はスピード重視、テストや設計は後回し。生成AIや属人化が進んでいる。
- 丁寧に構築するチーム:設計・レビュー・CI体制を整備済み。リリースはやや遅いが品質が安定。
4.2 シミュレーション結果
以下のグラフは、上記パラメータに基づき、
ChatGPTがシミュレーションに使ったコード
import numpy as np
import matplotlib.pyplot as plt
# 時間軸
t = np.linspace(0, 36, 500)
# ロジスティック成長モデル + 減衰項
def R(t, K, A, r, alpha):
return (K / (1 + A * np.exp(-r * t))) * np.exp(-alpha * t)
# 雑に速く作るパターン
params_fast = {
'K': 100,
'A': 2.0,
'r': 0.6,
'alpha': 0.08,
}
# 丁寧に構築するパターン
params_careful = {
'K': 100,
'A': 4.0,
'r': 0.3,
'alpha': 0.02,
}
# 計算
R_fast = R(t, **params_fast)
R_careful = R(t, **params_careful)
# プロット
plt.figure(figsize=(10, 6))
plt.plot(t, R_fast, label='Fast & Rough', color='red', linewidth=2)
plt.plot(t, R_careful, label='Careful & Structured', color='blue', linewidth=2)
plt.xlabel('Time (months)')
plt.ylabel('Growth Score R(t)')
plt.title('Product Growth Simulation Comparison')
plt.legend()
plt.grid(True)
plt.tight_layout()
# 保存
output_path = "/mnt/data/growth_simulation_comparison.png"
plt.savefig(output_path)
output_path
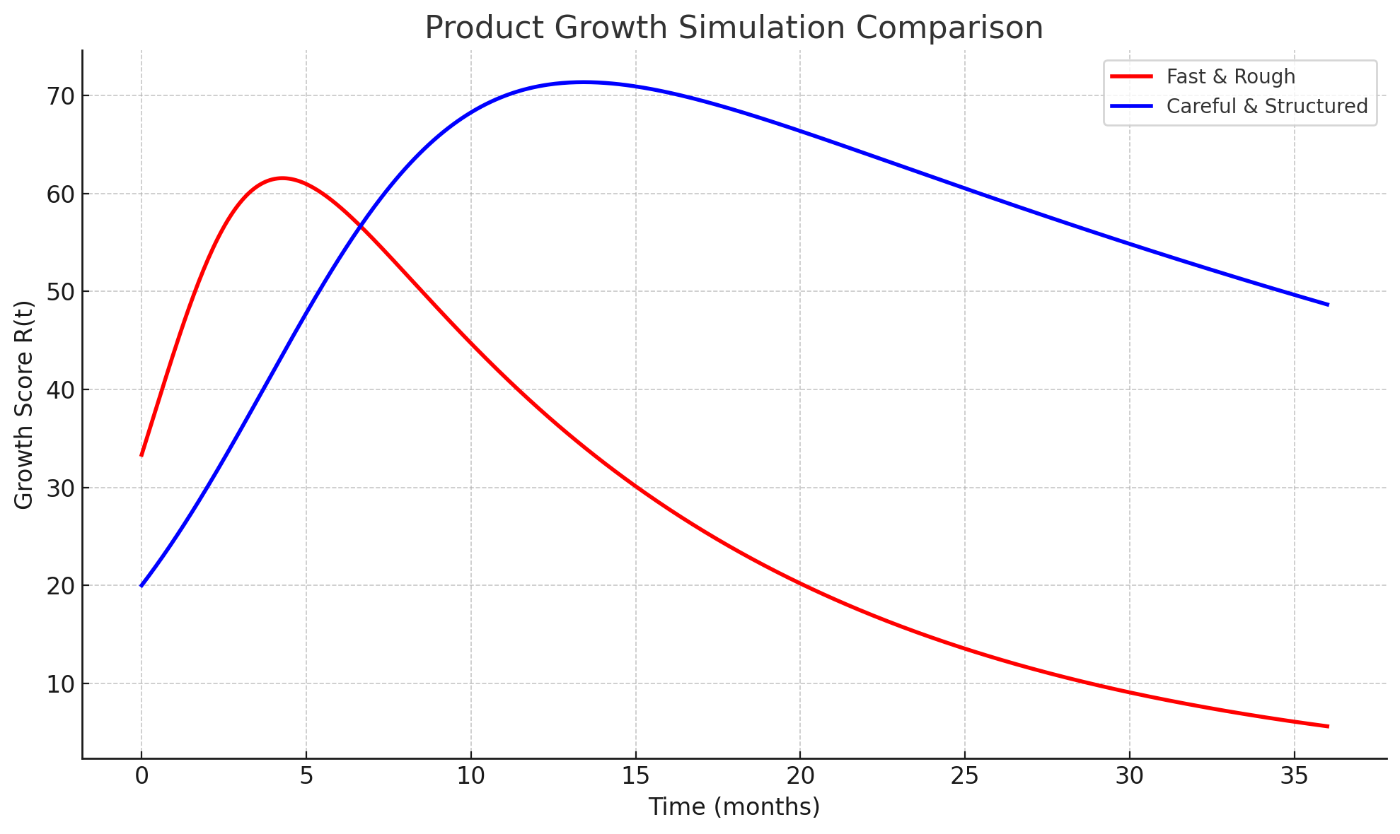
- 赤線:雑に速く作った場合 (Fast & Rough)
- 青線:丁寧に構築した場合 (Careful & Structured)
グラフから読み取れるように、雑に作った場合は初期成長が急激ですが、12ヶ月前後から失速傾向が強まり、その後は停滞・低迷へと向かいます。一方で、丁寧に作った場合は初期こそ緩やかですが、成長の持続性が高く、長期的に安定した成果を出しやすい傾向があります。
5. 考察と戦略的示唆
前章で示したシミュレーション結果から、プロダクト成長と技術的健全性の関係について、いくつか重要な示唆が得られます。
5.1 成長曲線の分岐点=改善フェーズ突入の兆候
シミュレーション上、雑に速く作った場合は 6〜12ヶ月 程度で成長が頭打ちになります。これには以下のような「兆候」が現れます:
- 機能ごとの開発サイクルが徐々に長くなってくる
- バグ修正や障害対応の頻度が上がる
- 要件定義や仕様のすり合わせに時間がかかるようになる
- Pull Request が滞留しがちになり、レビューの負荷が集中する
これらは、モデル上でいうと
さらに、丁寧に構築する場合が雑に早く作った場合を逆転するタイミングについて次の二つの観点から考えてみます。
①瞬間的な逆転
瞬間的な逆転は、前章のグラフにある青線と赤線の比(Careful / Fast)が1を超えるタイミングで確認できます(下図)。今回の結果だと約6.7ヶ月になります。

②累積貢献での逆転
下図における1枚目のグラフは、各アプローチで構築した時の

5.2 なぜ「丁寧に作っても」逓減するのか?
前章のシミュレーションでは、「雑に速く作る」「丁寧に構築する」いずれのアプローチでも、最終的には
これは、逓減(成長の減速)はアプローチに関係なく、時間の経過とともに必ず起こるということを示しています。
実際のプロダクト開発でも、以下のような要因によって成長は自然と鈍化していきます:
- 市場の飽和:新規ユーザーが取り尽くされる
- プロダクトの陳腐化:価値提案が古くなる
- チームの摩耗:速度や改善力が落ちる、離職やモチベーション低下
- 競合や外部要因:環境変化で勢いを失う
どれだけ丁寧に設計しても、こうした外的・内的要因によって逓減は避けられない現象として現れます。
モデル上では、これを 減衰率
- 雑に作れば
\alpha - 丁寧に作れば
\alpha
という違いはありますが、どちらも逓減は起こる設計です。
ただし、これを乗り越える方法も存在します。
-
技術改善の継続:
\alpha \alpha \alpha(t) -
市場の拡張や転換:
K K K(t)
このような再成長を捉えるには、2段階のS字モデルやシグモイド連結モデルといった設計も有効です。
5.3 プロセス改善施策の相互補完関係
成長の逓減を抑えるためには、技術的負債の発生スピード=減衰率
そこで有効になるのが、以下のような開発プロセス改善施策です:
| 施策 | 寄与する範囲 | 対象パラメータ | 特徴と限界 |
|---|---|---|---|
| ペアプロ | 設計・実装の品質向上、属人性排除 | 主に |
「負債の発生率」を抑えるが、コスト・相性問題も |
| 生成AI(Devin, CodeRabbit等) | 実装・修正の速度向上 |
|
補助的には強力だが、構造判断には不向き |
| コーディングルール制定 | チーム間の仕様統一、レビュー効率向上 |
|
継続運用と合意形成が前提条件となる |
ここで注目すべきなのは、これらの施策は単体で完結するものではなく、相互に補完し合うという点です。
- ペアプロで設計品質・共有度を上げつつ
- 生成AIで反復的・定型的作業を高速化し
- ルール化・レビューフローで再現性のある設計と品質を担保する
というように、並列的に併用することで、初期スピードと長期耐性を同時に実現することが可能になります。
5.4 「プロセス統合型ハイブリッド」戦略のすすめ
「ハイブリッド開発」という言葉はしばしば混同されがちですが、本記事が提案するのは以下の戦略です:
❌ よくある「PoCは雑に→後でちゃんと作る」型(フェーズ分割型)
- 初期スピードは出るが、組織やコードベースに分断・リスクを残しやすい
- 組み直しコストが大きく、再設計が途中で頓挫しやすい
✅ 本記事の提案:「プロセス統合型ハイブリッド」
- 初期からペアプロ・レビュー・生成AIなどを適切に併用
- 構造的健全性を犠牲にせず、速度を支える設計にする
- 成長曲線の持続性(
\alpha r
このアプローチの本質は、「改善前提で雑に作る」のではなく、「改善の起きにくい設計を初期から目指す」ことにあります。
その結果、改善フェーズへの突入が遅らせられ、突入後の改善コストも最小化される可能性が高まります。
6. 今後の戦略とまとめ
ここまで見てきたように、プロダクトの成長には「限界」と「減衰」がつきものです。だからこそ、ただ速く作るだけではなく、どうすれば成長を続けられるかを考える視点が大事になります。数理モデルを通じて見えてきたこととして、
- プロダクトの成長には限界(
K \alpha - 技術的負債や開発プロセスの設計が、成長の鈍化に直結する
- 数式を使えば、「いつ改善フェーズに入るか?」を感覚ではなく、データとして捉えられる
今回の記事では、「技術負債が成長にどう影響するのか?」という問いに対して、ロジスティック成長モデルをベースに考えてみるというアプローチを取りました。
もちろん、現実は数式だけで語り切れないこともたくさんあります。でも、こうしてモデルに落とし込んでみることで、「なんとなくの感覚」がチームで共有できる言葉や判断基準になるかもしれません。
Discussion