【Idris】自然数の型を定義して「∀n∈N. n+0=n」を証明する
自然数の型を定義しよう
Idrisには自然数の型である Nat 型が存在しますが、標準の Nat 型を用いずにデータ型 MyNat を自作してみましょう。定義は以下の通りです。
data MyNat = Zero | Succ MyNat
型 MyNat は Zero または Succ MyNat のいずれかの値をとります。 MyNat の定義に MyNat が使用されていますね。値が再帰的に定義されており、以下のように構成されていきます。
data MyNat = Zero | Succ MyNat
= Zero | Succ Zero | Succ (Succ MyNat)
= Zero | Succ Zero | Succ (Succ Zero) | Succ (Succ (Succ MyNat))
= .....
確かに 0, 1, 2, ... と対応していることが分かりますね!
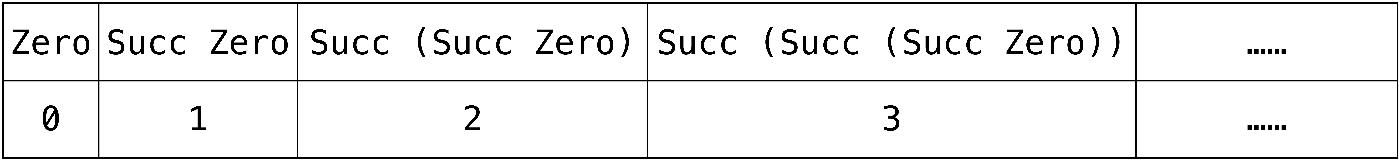
自然数の足し算を定義しよう
自然数の足し算を計算する関数 mynat_plus を定義します。 MyNat 型の引数を2つ受け取り MyNat 型の値を返すので、型シグネチャは次のようになります。
total mynat_plus : MyNat -> MyNat -> MyNat
第一引数の値で場合分けしましょう。第一引数が Zero の場合は第二引数をそのまま返します。
total mynat_plus : MyNat -> MyNat -> MyNat
mynat_plus Zero y = y
第一引数が Succ x (1以上の自然数)の場合は再帰的に定義します。
total mynat_plus : MyNat -> MyNat -> MyNat
mynat_plus Zero y = y
mynat_plus (Succ x) y = Succ (mynat_plus x y)
mynat_plus の引数に着目したときに、第一引数が1つ小さくなっていることが分かります。

第一引数が1つ小さい mynat_plus が再帰的に呼び出されることと、 mynat_plus Zero y が定義されていることから、関数 mynat_plus はいずれ停止することが保証されます。
それでは、関数 mynat_plus を実際に動かしてみましょう。
$ idris2 MyNat.idr
Main> mynat_plus (Succ Zero) (Succ Zero)
Succ (Succ Zero)
よく「1+1=2を証明して?」みたいなこと言われますよね。
mynat_plus (Succ Zero) (Succ Zero)
= Succ (mynat_plus Zero (Succ Zero))
= Succ (Succ Zero) Q.E.D.
この計算仮定を示してやりましょう!!
0+n=nを証明しよう
ん?タイトルの n+0=0 の証明とは異なるのでしょうか?そうです、(今回の mynat_plus の定義では)若干異なります。実際にやってみながら確認していきましょう。命題:「すべての自然数
total first_proof : (n : MyNat) -> mynat_plus Zero n = n
まず、 first_proof に add-clause コマンドを適用します。 add-clause コマンドによって、 first_proof の最初のパターンマッチが生成されます。
total first_proof : (n : MyNat) -> mynat_plus Zero n = n
first_proof n = ?first_proof_rhs
ここで、 ?first_proof_rhs に type-of コマンドを適用します。 type-of コマンドによって ?first_proof_rhs の型が出力されます。
n : MyNat
------------------------------
first_proof_rhs : n = n
あら、 n=n となっていますね。これはIdris側が mynat_plus Zero n を計算して n に置き換えてくれています。
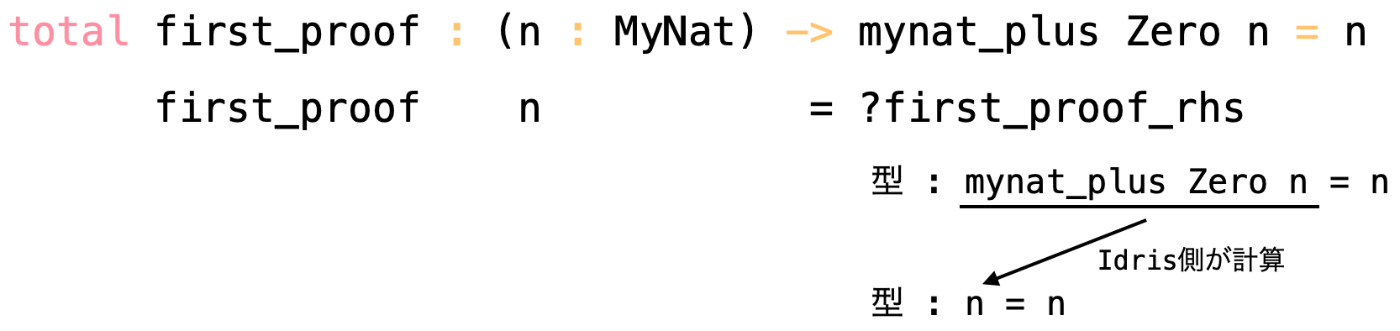
mynat_plus の定義からも分かるように、第一引数が Zero の場合は第二引数が返り値となるので、 mynat_plus Zero n は自明に n と等しいということですね。したがって、 ?first_proof_rhs を型 n=n の値 Refl に置き換えて証明完了です。
total first_proof : (n : MyNat) -> mynat_plus Zero n = n
first_proof n = Refl
n+0=nを証明しよう
命題「すべての自然数
total second_proof : (n : MyNat) -> mynat_plus n Zero = n
まずは同様に、 second_proof に add-clause コマンドを適用します。
total second_proof : (n : MyNat) -> mynat_plus n Zero = n
second_proof n = ?second_proof_rhs
そして「?second_proof_rhs を型 n=n の値 Refl に置き換えちゃいましょう!
total second_proof : (n : MyNat) -> mynat_plus n Zero = n
second_proof = Refl
あ、、、怒られてしまいました。

n と mynat_plus n Zero の間の制約が解けない(等価性の証明が与えられない)ようです。Idrisの気持ちになって、関数 mynat_plus の定義から mynat_plus n Zero を計算してみましょう。んー、できないですね。定数は計算してくれますが、変数が絡むと難しいみたいですね。では、どのように証明をすれば良いでしょうか?
数学的帰納法を用います。
①
mynat_plus Zero Zero = Zero
ここで、
mynat_plus k Zero = k
②
mynat_plus (Succ k) Zero = Succ (mynat_plus k Zero) (mynat_plusの定義より)
= Succ k (仮定より)
①, ②からすべての自然数
数学好きな皆さんにはお馴染みの証明ですね。以上の証明をプログラムに落とし込むと次のようになります。
total second_proof : (n : MyNat) -> mynat_plus n Zero = n
second_proof Zero = Refl
second_proof (Succ k) =
let hyp = second_proof k -- 帰納法の仮定
in ?hole1
let で変数を定義することで in の中で使うことができます。ここで、 type-of コマンドを使用して ?hole1 の型をみてみましょう。
k : MyNat
hyp : mynat_plus k Zero = k
------------------------------
hole1 : Succ (mynat_plus k Zero) = Succ k
仮定 hyp から mynat_plus k Zero と k が等しいことが使えるので、 hole1 : Succ (mynat_plus k Zero) = Succ k の mynat_plus k Zero を k に書き換えればいいですね!
どうやって? rewrite を使います。( let と同様に in の中で使われます。)
total second_proof : (n : MyNat) -> mynat_plus n Zero = n
second_proof Zero = Refl
second_proof (Succ k) =
let hyp = second_proof k -- 帰納法の仮定
in rewrite hyp in ?hole2
最後に ?hole2 の型をみてみましょう。
k : MyNat
hyp : mynat_plus k Zero = k
------------------------------
hole2 : Succ k = Succ k
よし!きた!!型 Succ k = Succ k の値 Refl に書き換えれば証明完了です!
total second_proof : (n : MyNat) -> mynat_plus n Zero = n
second_proof Zero = Refl
second_proof (Succ k) =
let hyp = second_proof k -- 帰納法の仮定
in rewrite hyp in Refl
おわりに
誤りや誤解を生みかねない表現などがありましたら、ご指摘よろしくお願いいたいします。
参考文献
- Introduction to Dependent Types with Idris
- Type-driven Development with Idris


Discussion