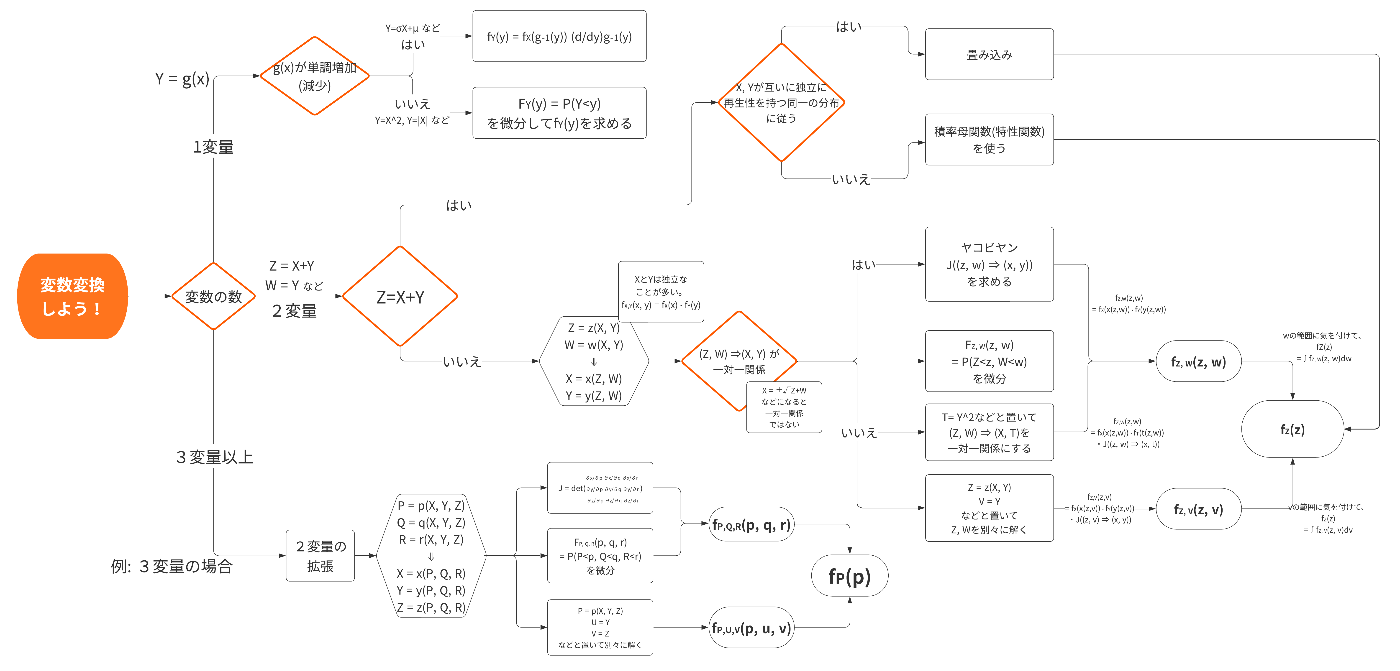
はじめに
「現代数理統計学の基礎」の演習問題を解いていく中で、変数変換を脳死でできないかと思い記事にしました。
確率変数が1個の場合
単調増加(減少)の場合
まず以下のような変形をする。
上の式を y で微分して
を求める。
上の二つを以下の公式に突っ込む。
f_{Y}(y) = f_{X}(g^{-1}(y))×|\frac{d}{dy}g^{-1}(y)|
まとめ
-
X= の形にする
- その式を y で微分する
- f_Y(y)=f_X(1.の右側)×(2.で求めたもの)
具体例
問題
f_{X}(x)=λe^{-λx} (x>0)\\
Y=σX+μ \\
⇩ \\
f_{Y}(y)
解答
まず、g^{-1}(Y), \frac{d}{dy}g^{-1}(y) を求める。
X=\frac{Y-μ}{σ}=g^{-1}(Y)\\
\frac{d}{dy}g^{-1}(y)=\frac{1}{σ}
より、
f_{Y}(y)=f_{X}(\frac{y-μ}{σ})×\frac{1}{σ}=λ\exp\{-λ(\frac{y-μ}{σ})\}
単調増加(減少)じゃない場合
分布関数 F_{Y}(y) を微分して f_{Y}(y) を求める。
まずは F_Y(y) を F_X(・) を使って表現する。
\begin{aligned}
F_Y(y) &= P[Y\leq y]\\
&= P[g(X)\leq y]\\
&= P[X\leq h_1(y)]+P[X\leq h_2(y)]\\
&= F_X(h_1(y))+F_X(h_2(y))
\end{aligned}
F_X(x) を求める。
F_X(x) = \int_{-∞}^{x}f_X(x) dx
F_X(x) から F_Y(y) を求め、y で微分することで f_Y(y) を求める。
F_Y(y) = F_X(h_1(y))+F_X(h_2(y)) \\
f_Y(y) = \frac{d}{dy}F_Y(y)
まとめ
-
F_Y(y) を F_X(.) を使って表す。
-
F_X(x) を求める。
-
F_Y(y) を求めて、yで微分する。
具体例
問題
f_{X}(x)=e^{x}, (-∞<x<∞)\\
Y=X^{2} \\
⇩ \\
f_{Y}(y)
解答
{\begin{aligned}
F_Y(y)&= P[Y\leq y]\\
&= P[X^2\leq y]\\
&= P[-\sqrt{y}\leq X \leq\sqrt{y}]\\
&= P[X \leq\sqrt{y}] - P[X \leq -\sqrt{y}]\\
&= F_X(\sqrt{y}) - F_X(-\sqrt{y})
\end{aligned}
}
{\begin{aligned}
F_X(x)
&= \int_{-∞}^xe^{t} dt\\
&= [e^{t}]_{-∞}^x\\
&= e^x
\end{aligned}
}
F_Y(y) = e^{\sqrt{y}}-e^{-\sqrt{y}}
{\begin{aligned}
f_Y(y)
&= \frac{d}{dy}F_Y(y)\\
&= (e^{\sqrt{y}}-e^{-\sqrt{y}})^{'}\\
&= \frac{1}{2\sqrt{y}}e^{\sqrt{y}}+\frac{1}{2\sqrt{y}}e^{-\sqrt{y}}\\
&= \frac{1}{2\sqrt{y}}(e^{\sqrt{y}}+e^{-\sqrt{y}})
\end{aligned}
}
※単調減少と単調増加に分けてから公式を割り当てていると考えるとわかりやすいかも。⇩
{\begin{aligned}
F_Y(y)&= P[Y\leq y]\\
&= P[X^2\leq y]\\
&= P[-\sqrt{y}\leq X \leq\sqrt{y}]\\
&= P[-\sqrt{y}\leq X \leq 0] + P[0 \leq X \leq \sqrt{y}]\\
&= \{F_X(0)-F_X(-\sqrt{y})\} + \{F_X(\sqrt{y})-F_X(0)\}\\
&= F_X(\sqrt{y}) - F_X(-\sqrt{y})
\end{aligned}
}
確率変数が2個の場合
\left\{
\begin{array}{ll}
Z=z(X, Y) \\
W=w(X, Y)
\end{array}
\right.
まず、以下のような変形を行う。
{\begin{cases}
Z=z(X, Y) \\
W=w(X, Y)
\end{cases}\Leftrightarrow
\begin{cases}
X=x(Z, W) \\
Y=y(Z, W)
\end{cases}
}
(Z, W) ⇒(X, Y) が一対一関係の場合
例: \\
X, Yは互いに独立で、X, Y~exp(λ)\\
{\begin{cases}
Z=X+Y \\
W=Y
\end{cases}\Leftrightarrow
\begin{cases}
X=Z-W \\
Y=W
\end{cases}
}
ヤコビヤン J((z, w) ⇒ (x, y)) を求める。
J((z, w) ⇒ (x, y))=
det\begin{pmatrix}
\frac{∂x}{∂z} & \frac{∂x}{∂w} \\
\frac{∂y}{∂z} & \frac{∂y}{∂w}
\end{pmatrix}
ヤコビヤンのコツ
-
(z,w) を見て「左の列が ∂z、 右の列が ∂w 」と覚えると良い。あとは普通に考えてxが上、yが下。
-
x,y で微分するか、z,w で微分するかわからなくなる人は、もう上の書き方をコピーして、z,w で微分してください。
- 上でやると、ヤコビヤンを使うときに逆数をとる必要がない(ただかけるだけ)なのでわかりやすいです。
f_{Z,W}(z,w)をヤコビヤンを使って求める。
{\begin{aligned}
f_{Z,W}(z,w)
&= f_{X,Y}(x(z,w),y(z,w))×|J|\\
&= f_X(x(z,w))×f_Y(y(z,w))×|J| (X,Y は互いに独立)
\end{aligned}
}
w の範囲を求める。
上の例だと、\\
(0 ≤ z-w ≤ ∞, 0 ≤ w ≤ ∞)\\
\Leftrightarrow
(w ≤ z ≤ ∞, 0 ≤ w ≤ ∞)
より、
となる。
w の範囲で f_{Z,W}(z,w) を積分して f_Z(z) を求める。
f_Z(z) = ∫f_{Z,W}(z,w) dw
まとめ
-
X=, Y=の形に変形する
-
ヤコビヤン J((z, w) ⇒ (x, y)) を求める。
-
f_{Z,W}(z,w)をヤコビヤンを使って求める。
-
w の範囲を求める。 ⇐ 忘れがち!!!
-
w の範囲で f_{Z,W}(z,w) を積分して f_Z(z) を求める。
具体例
問題
X, Yは互いに独立で、X, Y~N(0,1)\\
{\begin{cases}
Z=X+Y \\
W=Y
\end{cases}
}
f_X(x)=\frac{1}{\sqrt{2π}}exp(-\frac{x^2}{2})
解答
{\begin{cases}
Z=X+Y \\
W=Y
\end{cases}\Leftrightarrow
\begin{cases}
X=Z-W \\
Y=W
\end{cases}
}
{\begin{aligned}
J((z, w) ⇒ (x, y))
&= det\begin{pmatrix}
\frac{∂x}{∂z} & \frac{∂x}{∂w} \\
\frac{∂y}{∂z} & \frac{∂y}{∂w}
\end{pmatrix}\\
&= det\begin{pmatrix}
1 & -1 \\
0 & 1
\end{pmatrix}\\
&= 1
\end{aligned}
}
{\begin{aligned}
f_{Z,W}(z,w)
&= f_X(z-w)×f_Y(w)×1\\
&= \frac{1}{\sqrt{2π}}exp\{-\frac{(z-w)^2}{2}\} × \frac{1}{\sqrt{2π}}exp(-\frac{w^2}{2})\\
&= \frac{1}{2π}exp\{-\frac{(z-w)^2+w^2}{2}\}
\end{aligned}
}
(-∞≤z-w≤∞, -∞≤w≤∞)\\
\Leftrightarrow(-∞≤z≤∞, -∞≤w≤∞)\\
{\begin{aligned}
f_Z(z)
&= \int_{-∞}^∞\frac{1}{2π}exp\{-\frac{(z-w)^2+w^2}{2}\}dw ⇒方針: wについての正規分布の確率密度関数の形にして1で消す\\
&= \frac{1}{2π}\int_{-∞}^∞exp\{-\frac{2w^2-2zw+z^2}{2}\}dw\\
&= \frac{1}{2π}\int_{-∞}^∞exp\{-\frac{2(w-\frac{z}{2})^2-\frac{z^2}{2}+z^2}{2}\}dw\\
&= \frac{1}{\sqrt{2}}\frac{1}{\sqrt{2π}}exp(-\frac{z^2}{4})\int_{-∞}^∞\frac{1}{\sqrt{2π(\frac{1}{\sqrt{2}})^2}}exp\{-\frac{(w-\frac{z}{2})^2}{2×(\frac{1}{\sqrt{2}})^2}\}dw\\
&= \frac{1}{\sqrt{2π(\sqrt{2})^2}}exp(-\frac{z^2}{2×(\sqrt{2})^2})
\end{aligned}
}
よって、
(Z, W) ⇒(X, Y) が一対一関係じゃない場合
例:
{\begin{cases}
Z=X+Y \\
W=XY
\end{cases}\Leftrightarrow
\begin{cases}
Z=X+Y \\
W=X(Z-X) ⇐一意に定まらない
\end{cases}
}
ZとWを別々で解く
上の例でやると、
{\begin{cases}
Z=X+Y \\
V=Y
\end{cases}\Leftrightarrow
\begin{cases}
X=Z-V \\
Y=V
\end{cases}
}
{\begin{cases}
W=XY \\
U=Y
\end{cases}\Leftrightarrow
\begin{cases}
X=\frac{W}{U} \\
Y=U
\end{cases}
}
として、別々にヤコビヤンなりを求めて解けばよい。
ZとWの分布関数 F_{Z,W}(z, w) を微分する
XやYを別の確率変数に置き換えて、一対一関係にする
例: \\
X,Y ~N(0,1)\\
{\begin{cases}
Z=X^2+Y^2 \\
W=\frac{Y}{\sqrt{W}}
\end{cases}\Leftrightarrow
\begin{cases}
X=Z\sqrt{W} \\
Y=±\sqrt{W(1-Z^2)}
\end{cases}
}
ここで、
と置くと、
{\begin{cases}
X=Z\sqrt{W} \\
T=W(1-Z^2)
\end{cases}
}
となり、(Z, W) ⇒(X, T) が一対一関係になる。
おまけ: 確率変数の和の分布を2つの手法で解く
X, Yは互いに独立、X~Po(λ_1), Y~Po(λ_2)\\
Z=X+Y
- 畳み込み
- 積率母関数(または特性関数)
を使って解く。
畳み込み
まず、
とおく。
{\begin{cases}
Z=X+Y \\
W=Y
\end{cases}\Leftrightarrow
\begin{cases}
X=Z-W\\
Y=W
\end{cases}-①
}
となる。
ヤコビヤン J ((z, w) ⇒ (x, y)) は、
det\begin{pmatrix}
1 & -1 \\
0 & 1
\end{pmatrix}
= 1-②
であるので、wの範囲をW_{area}とすると、
f_Z(z) = ∫_{W_{area}}f_X(z-w)・f_Y(w) dw
と書ける。この時、上の①②を省いてここまで辿り着ける。
要するに、
- XとYが独立で、その和(X+Y)の確率関数を求めよ、という問題を見る
-
W_{area}を求める。
-
f_Z(z) をf_Z(z) = ∫_{W_{area}}f_X(z-w)・f_Y(w) dw で求める。
で終わる。
特徴
- 理論上、X,Yが(独立であれば)どんな分布でもZを求めることはできる。
- しかし、上の3. の部分の計算が複雑になり手計算では到底解けないことがあるため、その時は次の積率母関数を使った解法等を考えるべき。
- また3変量以上の場合、重積分になるため計算くそだる。
- 2変量の和の変数変換を脳死でやるにはまずはこっちかな。
積率母関数
積率母関数は、
で得られ、X, Y が互いに独立で、Z=X+Yの積率母関数を求める時、
M_Z(t) = E[e^{tZ}] = E[e^{t(X+Y)}] = E[e^{tX}]・E[e^{tY}] (X,Yが独立)
となる。要するに、
- X,Yの積率母関数を別々で求める。
- それらを全て掛け合わせることでZの積率母関数 M_Z(t) になる。
-
M_Z(t) が既知の確率分布の積率母関数になったらZの分布もそれなので、記憶から確率密度関数を呼び起こしてください。
特徴
- 使える場面は限られる(積率母関数が既知の形の時)が、使えるときは楽にZの分布が分かりがち。
- X, Yが「互いに独立に、再生性を持つ同一の分布に従う」時は迷いなくこっち。
- 3変量以上でも全然使える。てか、3変量以上で和の変数変換だったら積率母関数をまず考えよう。
- しかし、いざ M_Z(t) を求めて全然知らん形になったときは絶望の嵐。その時は楽せず畳み込みをしましょう。
※ 再生性の例
N(μ_1, σ_1^2)+N(μ_2, σ_2^2) = N(μ_1+μ_2, σ_1^2+σ_2^2)
どっちの解法を使うべき?
前提: 互いに独立な確率変数の和の形 X+Y(+Z+...) の分布を求める。
- 「3変量以上」または「X, Y, ...が互いに独立に、再生性を持つ同一の分布に従う」ときは積率母関数!
- それ以外は畳み込み!で良い!
- 上の条件がなくても M_Z(t) が何かの確率分布の積率母関数になりそう…!!!という神のお告げが聞こえたら、確率母関数使ってもいいです。
問題
X_1, ..., X_nが互いに独立\\
i=1, ..., nに対し、X_i ~ Po(λ_i)の時\\
Σ_{i=1}^{n}X_iの従う分布を求めよ。
解答
{\begin{aligned}
M_Z(t)
&=E[e^{tz}]=E[e^{tΣ_{i=1}^nx_i}]\\
&=E[e^{tx_1}]...E[e^{tx_n}](X_1,...,X_nが互いに独立)
\end{aligned}
}
E[e^{tx_i}]=M_{X_i}(t)=exp\{(e^t-1)λ_i\}
{\begin{aligned}
M_Z(t)
&=exp\{(e^t-1)λ_1\}...exp\{(e^t-1)λ_n\}\\
&=exp\{(e^t-1)(λ_1+...+λ_n)\}\\
&=exp\{(e^t-1)Σ_{i=1}^nλ_i\}
\end{aligned}
}
したがって、
Σ_{i=1}^{n}X_i~Po(Σ_{i=1}^nλ_i)
参考文献
『現代数理統計学の基礎』(久保川達也 著)

Discussion