🍣

記号だけでシェルピンスキーのギャスケットを描く

2024/12/11に公開

Bash

shell

tech

はじめに

シェルスクリプトで雪の結晶を描くという記事を書いた。

この記事には頭がおかしいスクリプトしか出てこないのだが、その中でもとくにイカレてるのが、シェルピンスキーのギャスケットと呼ばれるフラクタル図形を描画する以下のシェルスクリプトである(元記事から1ヶ所修正した部分がある。詳しくは後述)。

! _(){
((____=__,${_______=_____[____]^=_____[____-__],++____<___&&_______}))
$______<<<${_____[@]}
((++________<___))&&_
}
_____=(${__=$?})
___=$[__<<$__$?-__]
: /*/$$;: ${_:__:__}
(${______=/???/??[!$__]/?$[~__*~__]}<<<${_^}$__\ $___\ $___;_)|convert - -rotate 45 -trim sierpinski.png

記号ばっかり。アルファベットが使われている最後のconvertコマンドでは画像の回転とフォーマット変換しかしておらず、画像の出力としては記号ばっかりの部分だけで完結している(PBMという一般的でない形式だが)。

冒頭の画像は、このスクリプトで生成されたものである。

本記事では、このイカレたスクリプトについて解説する。

読みやすくする

シェルスクリプトは記号だけでチューリング完全である。[ ... ]と &&、||で条件分岐できるし、関数の定義は記号だけで可能だから、その再帰でループも実現できる。よって、記号だけでスクリプトを書くのはそんなに難しいことではない。

記号だけでシェルスクリプトを書く場合、変数名として使える文字は_だけである。したがって、複数の変数が必要になるスクリプトでは$__、$___、$____のように_を複数並べてその長さで区別することになる。なお、長さ1の$_は組込み変数として別の用途で使われているので使えない(後述)。

関数名は変数名ほど縛りはきつくなく、_以外の文字も使うことができる。が、実はシェルの実装によって使える記号が異なっているようで、互換性を考えるなら_以外の記号は使わないのが無難である。もっとも、今回のスクリプトはbash以外での動作を考慮していないので互換性を考える必要はないのだが。

そんなわけで、記号だけのシェルスクリプトは変数名などで_が頻出する宿命にある。さすがに読みづらいので、冒頭のスクリプトの変数と関数をてきとーな名前に置き換えてみよう。このようになる。

! main(){
((i=one,${loop=cell[i]^=cell[i-one],++i<size&&loop}))
$m4<<<${cell[@]}
((++j<size))&&main
}
cell=(${one=$?})
size=$[one<<$one$?-one]
: /*/$$;: ${_:one:one}
(${m4=/???/??[!$one]/?$[~one*~one]}<<<${_^}$one\ $size\ $size;main)|convert - -rotate 45 -trim sierpinski.png

もちろん、元のスクリプトとまったく同じ結果が得られる。

以下ではこれを元に順番に解説していく。

1-5行目

! main(){
...
}

冒頭の!は終了コード($?)を反転させる。コマンドが0で終了したなら$?が1に、0以外で終了したなら0になる。

!に続くのはシェル関数の定義。関数定義は通常0で終了するから、ここでは$?に1がセットされる。関数の中身については後述。

6行目

cell=(${one=$?})

変数の初期設定をしている。

${var=value}は、変数$varが未定義ならば$varにvalueを代入し、その後$varの値に展開される。$oneという変数はここまで定義されておらず、$?には前の行で1がセットされているから、${one=$?}は$oneという変数に1を代入するとともに、その値である1に展開される。

つまり、この行は

one=1
cell=(1)

と等価である。cell=(1)は配列変数$cellの最初の要素に1をセットする。

ところで、${var=value}という変数展開はmanに記載されていない、と勘違いする人がたまにいるが、そんなことはない。manには${var:=value}という形式で記載されていて、そこから少し離れたところに「コロンを省略した場合は」とちゃんと言及されている。${var=value}は「$varが未定義なら」だが、コロンのある${var:=value}は「$varが未定義または空文字列なら」という意味になる。

7行目

size=$[one<<$one$?-one]

この行では生成される画像のサイズを決めている。ここをてきとーにいじることで異なる大きさの画像を出力することが可能。

$[ ... ]は$(( ... ))と同じで、算術式展開をおこなう(厳密には展開の優先度が異なるのだが、今回のスクリプトでは関係ないので詳細は割愛する)。算術式の中では変数名に$がなくても値を参照できる。$oneは前の行で1が代入され、また前の行はただの代入でかならず成功するから終了コード$?の値は0である。よって、この行は以下の計算をおこなう。

size=$[1<<10-1]

<<はビット左シフト。この算術式はzshでは(1<<10)-1と解釈されて1023という値になるが、bashでは1<<(10-1)と解釈されて512になる。直感的にはzshのほうが正しそうなんだけれど、Cやpythonやrubyではbashと同じように解釈されるのでzshがおかしいんだろう。

なお、man bashしても$[ ... ]による算術式展開は記載されていない。${var=value}と異なり、これはマジモンのundocumentedである。といっても、実はbashの古いバージョンには記載があった(展開の優先度が異なることは古いmanにも書かれていない)。おそらくPOSIXにないし$(( ... ))があれば困らないのでmanの記載からは消して非推奨になったのだけれど、古いスクリプトがこの機能を使っているので機能自体を削除することはできなかったのだと思われる。

8行目

: /*/$$;: ${_:one:one}

:は何もしない組み込みコマンド。/bin/trueと同じで、かならず成功して終了コードが0になる以外には何もしない。:自体は何もしないが、シェルが$_という変数に「直前のコマンドの最後の引数」をセットする。

たとえば、コマンドラインで

% mkdir newdirectory

を実行すると、$_にnewdirectoryという値がセットされる。よって、その後

% cd $_

を実行することで作成したディレクトリに移動できる。

/*/$$はワイルドカード展開。$$はシェルのプロセスIDだから、/*/$$は、Linuxではほとんどの場合/proc/<process_id> というディレクトリにマッチし、$_にこの文字列がセットされる。

後半の: ${_:one:one}は、またしても何もしない:である。

${var:offset:length}は$varから文字列の部分切り出しをおこなう。offsetとlengthは算術式として扱われるので、変数を参照する場合でも$は不要である。$oneの値は1だから、これは${_:1:1}となる。offsetは0-originなので、$_の2文字目から1文字だけ切り出すことになる。$_の中身は/proc/<process_id>だから、その2文字目から1文字分、つまりpという文字が新たに$_にセットされる。

シェルスクリプトは記号だけでチューリング完全ではあるが、数字やアルファベットも必要である。数字はさまざまな方法で記号から作ることができるが、アルファベットは一筋縄ではいかない。いまのところ筆者は環境に依存せず記号だけからアルファベットを生成する方法を発見できていない。

今回はワイルドカードにマッチさせるという、ファイルシステムに依存する方法でアルファベットを生成している。ほかには、わざとエラーを発生させてそのエラーメッセージから必要な文字を取得するという方法もあるが、これはシェルのバージョンが変わるとメッセージが変更される可能性があるし、また同じバージョンでもlocaleによって異なる文字列になってしまうことがある。

9行目

(${m4=/???/??[!$one]/?$[~one*~one]}<<<${_^}$one\ $size\ $size;main)|convert - -rotate 45 -trim sierpinski.png

画像を生成する。

まず、

${m4=/???/??[!$one]/?$[~one*~one]}<<<${_^}$one\ $size\ $size

の部分。

$oneが1だから、$[~one*~one]の算術式は~1*~1の計算をおこなう。~は2の補数を取る前置演算子で、~1は-2。よって、かけ算すると4になる。そして、前述の${var=value}の構文により、$m4という変数に/???/??[!1]/?4という値がセットされる。この値をワイルドカードでマッチさせると、適切にインストールされていれば/usr/bin/m4が見つかるだろう。

実は、元記事ではこのワイルドカード展開を/???/??[!1]/?4ではなく/???/???/?4 としていた。ところが、一部の環境ではこれが /usr/bin/m4 だけでなく /bin/X11/m4 にもマッチしてしまうようだ。そこで、本稿では一部を[!1](1以外の任意の1文字にマッチ)に修正している。こういうことがよく起きるので、環境に依存せずアルファベットを生成する手段が求められるのだ。

<<<はヒアストリング。$m4の標準入力に${_^}$one\ $size\ $sizeという文字列を与えている。

${var^}は$varの先頭文字をアルファベット大文字に変換する。ちなみに${var^^}だと先頭だけでなくすべての文字が大文字になり、${var,}や${var,,}は小文字に変換する。

$_には前の行でpという値がセットされているから、${_^}はこれを大文字にしたPになる。全体として、P1 512 512という文字列が$m4の標準入力に与えられることになる。/usr/bin/m4はマクロプロセッサだが、とくにマクロを定義していないので、入力がそのまま、つまりP1 512 512という512x512ピクセルのPBM(ascii)形式画像のヘッダが出力される。

残りの部分。

(...;main)|convert - -rotate 45 -trim sierpinski.png

mainは1-5行目で定義したシェル関数の呼び出しで、画像データ本体を出力する。P1 512 512というヘッダと合わせて、PBM形式の画像になり、これがconvertコマンドで処理されてPNG形式で出力される。

main関数

main(){
((i=one,${loop=cell[i]^=cell[i-one],++i<size&&loop}))
$m4<<<${cell[@]}
((++j<size))&&main
}

画像を構成するそれぞれのピクセルの値を計算する本体部分である。

画像の横方向と縦方向のそれぞれに繰り返しが必要になるが、横方向は算術式の再帰評価で、縦方向はシェル関数の再帰で実現している。

横方向の繰り返しが2行目の算術式。

((i=one,${loop=cell[i]^=a[i-one],++i<size&&loop}))

${loop=...}はすでに何度か説明した${var=value}の変数展開。$oneは1、$sizeは512だから、これは

loop='cell[i]^=cell[i-1],++i<512&&loop'
((i=1,cell[i]^=cell[i-1],++i<512&&loop))

と同じである。

算術式中の,はシェルや他のプログラム言語における;のようなものと思ってもらってよい。そして、算術式中の文字列は、算術式とみなされて再帰評価される。loopの中に含まれる++i<512&&loopにより、iの値をインクリメントしながら512に達するまでloopを再帰評価しつづける。cell[i]^=cell[i-1]については後述。

算術式の再帰評価については、以下の記事が非常に詳しいので参照されたい。

3行目。

$m4<<<${cell[@]}

$cellは前の行で計算した横方向のピクセルの値が格納されている配列変数。${cell[@]}で配列の全要素に展開される。これをヒアストリングで/usr/bin/m4の標準入力に与えることで、画像の横1列を出力する。

4行目。

((++j<size))&&main

縦方向の繰り返し。jの値が512に達するまでインクリメントしながら自分自身を再帰呼び出しする。

Rule 90

ここまででまだ説明せず残っているのは、算術式中の

cell[i]^=cell[i-1]

の部分だけである。そして、まだシェルピンスキーのギャスケットについて一切触れていない。つまりこの式があのフラクタル図形を生成する本体である。

ライフゲームは承知のことと思う。ライフゲームでは、碁盤状の平面のあるマス(cell)とその周囲8マスの生死によってそのマスの次の世代の生死が決定される。このような「あるマスとその周囲のマスの状態によって次世代の状態が決定されるモデル」を一般化したのがセル・オートマトンである。

ライフゲームはマスが平面に広がっているので2次元セルオートマトンに分類される。そして、平面ではなく直線上のマスで状態を遷移させるのが1次元セルオートマトンである。シェルピンスキーのギャスケットは、1次元セルオートマトンのRule 90で生成できることが知られている。

Rule 90は、注目しているマスとその両隣のマスの状態により、そのマスの次の状態を以下のように遷移させる。

現在の状態	次の状態
1 1 1	0
1 1 0	1
1 0 1	0
1 0 0	1
0 1 1	1
0 1 0	0
0 0 1	1
0 0 0	0

「次の状態」を上から順に並べると、01011010となる。これを2進数とみなして10進数にすると、90になる。Rule 90と呼ばれるのはこれが理由である。

さて、この表をじっくり眺めていると、現在の状態が 1 1 1のときと1 0 1のとき、どちらも次の状態が0であることに気がつく。また、1 1 0と1 0 0も次の状態は1で同じである。さらによく見ると、A 0 BとA 1 Bはどちらも同じ状態に遷移することがわかる。Rule 90では、そのマスの現在の状態にかかわらず、両隣のマスの状態によってのみ、次の状態が決定されるのである。

そこで、上の表から注目しているマスの状態を省略したものを作ってみよう。

両隣の状態	次の状態
1 1	0
1 0	1
0 1	1
0 0	0

この表に見覚えはないだろうか。そう、これは排他的論理和(XOR)の真理値表そのものである。つまり、XORの演算子を ^とすると、マスの次の状態は

cell_next[i] = cell_current[i-1] ^ cell_current[i+1]

であらわせるのである。

1次元のセルの状態遷移を上から下に2次元状に配置すると、下の図のようにシェルピンスキーのギャスケットが出現する。それぞれのマスは、その左上と右上(前の世代の両隣)のXORをとったものになっているのがわかるだろうか。

この図を45度回転してみる。

元の図では上から下に世代が経過していたが、回転したこの図では左上から右下の方向に世代が経過していく。そして、元の図では「左上と右上のマスのXOR」だったが、回転したことにより「左と上のマスのXOR」になった。

これを式であらわすと以下のようになる。

cell[i] = cell[i-1] ^ cell[i]

さらにこれは

cell[i] ^= cell[i-1]

とあらわせる。つまり、碁盤目の左上に1を置き、あとはこの式をひたすら計算することでシェルピンスキーのギャスケットを描画することができる。

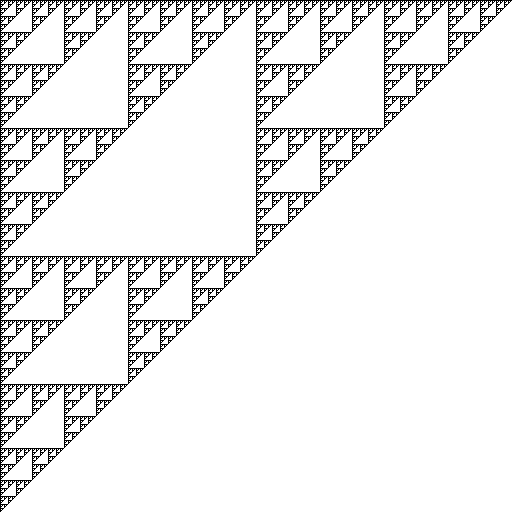
生成される画像は45度回転しているので、逆方向に45度回転してやると冒頭の画像が得られる。

おまけ

ということで、記号だけのシェルスクリプトで画像を生成してみた。

ところで記号だけでフラタクタル画像を生成するといえば、世の中にはすごい人がいるもので、8種類の記号だけしか使わないBrainfuckというクソ言語でマンデルブロ集合をアスキーアートで出力するプログラムを書いた人がいる。

自分にはそんな偉業はとうてい真似できないので、せめて自作のbrainfuckインタプリタでこのプログラムを実行してみた。

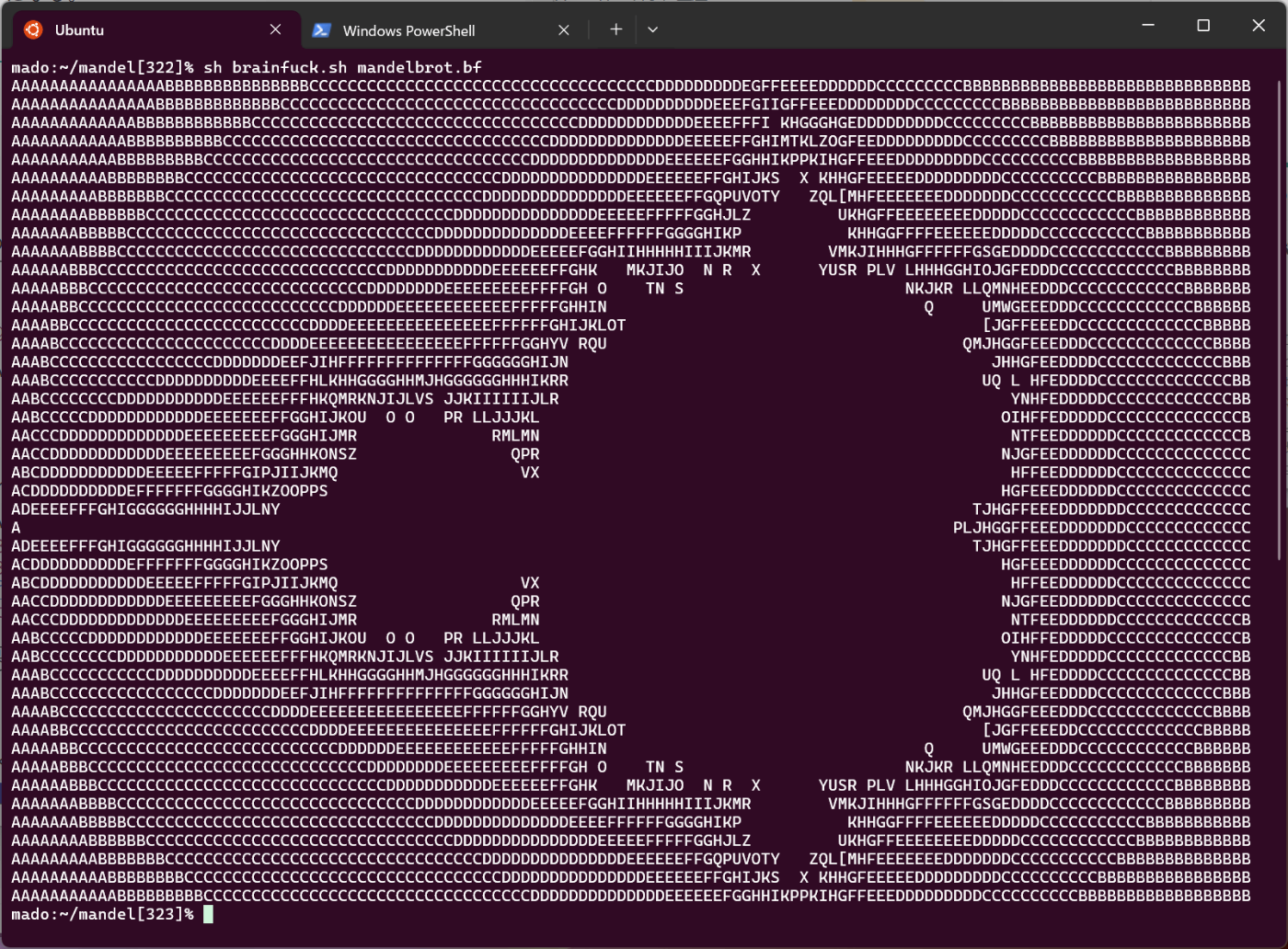
手元のマシンでだいたい3.5時間ぐらいかかった。

せっかくなのでこの結果をPNG画像に変換してみる。また3.5時間…。

% (echo P5 129 48 27; sh brainfuck.sh mandelbrot.bf | tr -d \\n | tr ' A-[' '\0-\27' ) | convert - mandelbrot.png

以下が上記結果を得るのに使ったbrainfuckのインタプリタ。POSIXの範囲内で書いている(bashの拡張機能を使っていない)ので、bashにかぎらずいろんな実装のシェルで動くと思われる。たぶん。

_(){ __=$@;}
_ /???
_ /??${__##*/??}/???/?${__##*/??}
____________=${__##*/}

________(){ $____________ " -<" _-{<<_
$@
_
}

______=$(________ "&$((${#?}$?+~${#?}-${#?}))\"-")
$______ $(________ "_____________=%%
___=#$((~${#?}*~${#?}))
____=\$$?$(((${#?}-~${#?})<<${#?}))/$((-${#?}$?/~${#?}))
_____=%&$((${#?}$?+~${#?}-${#?}))
___________=/$(((${#?}-~${#?})<<${#?}))--
__________=${#?}$((${#?}-~${#?}))*/$((-${#?}$?/~${#?}))'
________________=$((${#?}-~${#?}))&\"%
_______=$((~${#?}*~${#?}))&%
________=(
_______________=$((${#?}$?+~${#?})))*-&
_________=%$?
_________________=%$?/&
______________=&$((${#?}$?-${#?}))*$((-${#?}$?/~${#?}))")

_____________="$_____________ $___=${#?} $____=${#?} $((${#?}+${#?}))>/$_____/$___________"

___=$?
____=${#?}
_____=$((~____*~____)); _____=$((____<<_____<<_____))

__=$?
$______ _$?=$?

_(){
    $______ _$__=\$\(\(\(\$_$__+____\)%_____\)\)
}
__(){
    $______ _$__=\$\(\(\(\$_$__+_____-____\)%_____\)\)
}
___(){
    __=$((__+____))
    $______ : \${_$__=$___}
}
____(){
    [ $__ = $___ ] && $______________ $____
    __=$((__-____))
}
_____(){
    $__________ _ | $____________ _ \\$($______ $__________ %${_________#?} \$_$__)
}
______(){
    ___________=$($______ $_____________ | ${_________#?}${_________%?} -${_________%?} | { $________________ _ __ _; $__________ "$__";})
    [ _"$___________" = _ ] && $______________
    $______ _$__=$___________
}
_______(){
    $______ [ \$_$__ != $___ ]
}

$______ $($____________ -$(________ '%$') '<>[],.+-' < $($______ $__________ \$$____) | $_______ "
    ${_______%??}/\+/_;/$________
    ${_______%??}/-/__;/$________
    ${_______%??}/>/___;/$________
    ${_______%??}/</____;/$________
    ${_______%??}/\./_____;/$________
    ${_______%??}/,/______;/$________
    ${_______%??}/\[/$_______________ _______;$_________ /$________
    ${_______%??}/\]/$_________________;/$________
    ${_______%??}/;\$//")

はじめに

読みやすくする

1-5行目

6行目

7行目

8行目

9行目

main関数

Rule 90

おまけ

Discussion