🎰
個人がいつギャンブルを中止するのかについて ~経済学参照点依存損失回避 Jarque-Bera-Test ~

2025/06/09に公開
今回はこの論文についてです。経済学の文脈でギャンブラーの行動を分析した論文を調べていたらこれにあたりました。
Lien, J. W., & Zheng, J. (2015). Deciding When to Quit: Reference-Dependence over Slot Machine Outcomes. The American Economic Review, 105(5), 366–370. http://www.jstor.org/stable/43821910

ほぼ同じ内容のworking paperは以下から。

https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2636123
残念なことにデータとcodeが何一つ記載されていないので、シミュレーションデータと正規性検定のpythonコードを末尾に載せておきました。クソコですが興味があれば。Rも時間あるときに載せます！

 参照点依存と損失回避行動経済学においては、意志決定者は絶対的な結果よりも相対的な結果に強く価値を感じることが多く確認されています。

「いくら得た／失ったか」だけでなく、ある基準（参照点：reference-dependence）と比べてどうだったかによって満足度（効用）が変わります。

つまりギャンブルにおいては、ある日のギャンブル開始時点でのお財布のお金の量と比較して、金額が何%増えたか、あるいは何%減ったかで、満足度（効用）が変わる、という考え方が参照点依存です。

言い換えれば、その日のギャンブルが収支が何%プラスか/マイナスかということに人の満足度は左右されるという考え方です。
さらに、ミクロ経済学には損失回避(loss aversion)という概念があります。「金額水準Aからx円の利益の上昇」による満足度(効用)の増加量と比較して、「金額水準Aからx円の低下」による満足度(効用)の低下量の方が大きいと考えられています。


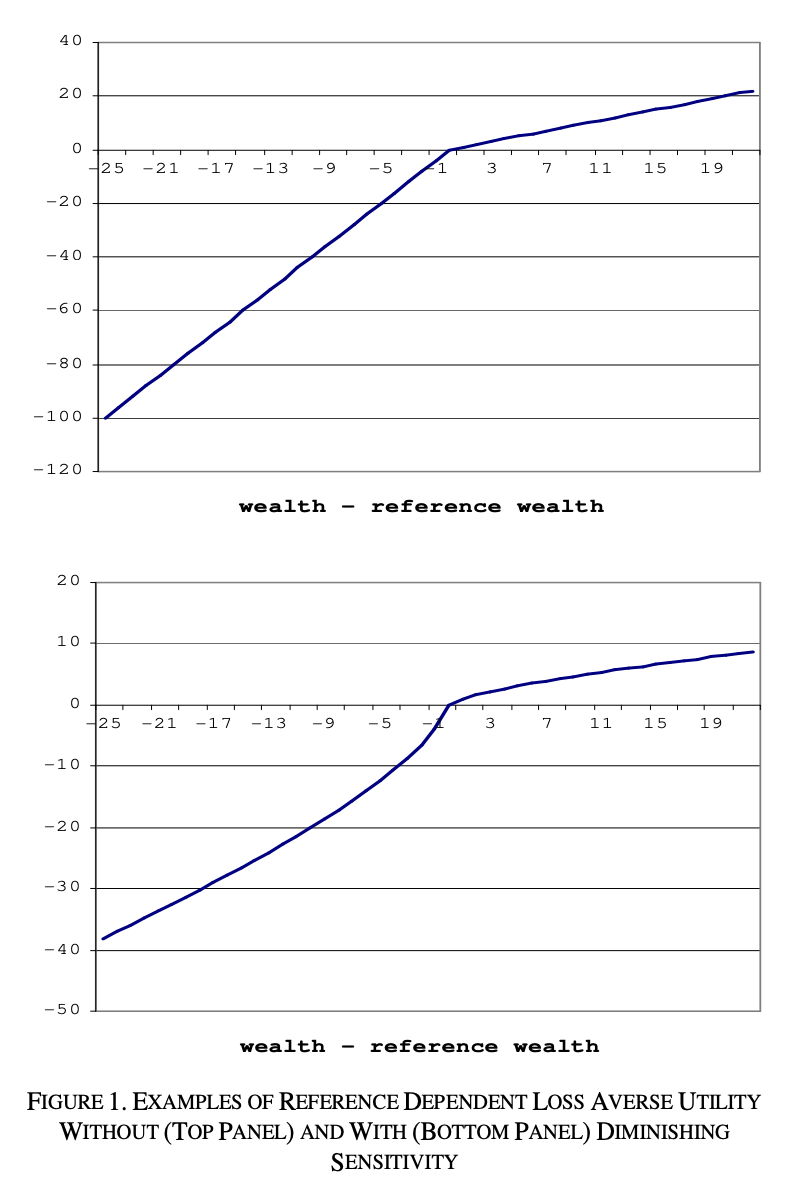
このグラフは、損失回避を表しており、縦軸が個人の満足度、横軸が財産を指しております。

（グラフの上下の違いは無視してもらって大丈夫です。）

棒グラフを観察すると、横軸が0からマイナス(左)に推移した途端、満足度の下がり方が大きくなることが見て取れます。
したがって、ある日のギャンブルの収支が±0の時点では、ギャンブラーはリスクを取り新たにベットを行い収支をプラスに持っていくよりも、その場でギャンブルをやめることを望ましく考える傾向にあるという考え方です。

 論文内容この論文はカジノのスロットでユーザーがその日の総収支がどの時点でギャンブルを辞めるのかという視点から参照依存点と損失回避について分析しています。
上記で述べた参照点依存と損失回避の考え方より、ギャンブラーが離脱する際の収支は0付近が多くなることが期待されます。「0付近」と書いたのは、ギャンブルがそもそも期待値マイナスのゲームであり、総収支はマイナスになることが期待されるからです。

 トピック➀
 目的ユーザーがスロットを中止するタイミングの総収支の値を知りたい。

 方法ユーザーのクロスセクショナルデータをつかって、ユーザーがギャンブル開始時点の所有金額に対して、その日のスロットを中止するときの金額はの分布を作成

 結果

ユーザーがスロットをやめるタイミングの収支は、プラスマイナス付近が多い。

上のヒストグラムでは、中止したタイミングのnet winnning(収支)が横軸、縦軸が頻度になっています。

この結果が示唆することは、globalな（どのギャンブラーにも共通の）参照依存点が存在するということです。

しかし、ギャンブルの性質上、（あたりまえですが）収支がマイナスで終わる人のほうが多いことも見て取れます。

次の分析では、いつ中止するかの判断が、個人の投資額(intensity)でどの程度変化するのかについて分析しています。

 トピック➁
 目的ユーザーを特徴付ける平均ベット額とベット回数でユーザーの参照点依存の変化を見る
なぜこの2つの変数に注目するのかというと、intensityは、平均ベット額とベットの回数を元に考えられます。

その日の合計投票額 = 平均ベット額×ベット回数で求められますね。

 方法bet回数と平均bet額のbinごとに、

実際の総収支の経験分布がシミュレーションによる正規分布から離れているのかについてJarque-Bera Testで検定する。

さらに、どの方向に経験分布が偏っているのかを調べるため、経験分布の過剰尖度と過剰尖度を導出し、正規分布にもとづくシミュレーションにより生成された分布との乖離の程度を調査する。
仮定：総収支(net winnings)は、中心極限定理より正規分布に従う。

Intensity \sim N(w \mu b, (w \sigma)^2 b)
w = 平均ベット額, b = 合計bet数, \mu = 単一のbetの期待値, \sigma^2 = 単一のbetの分散
総収支の分散は平均bet額wの二乗と、そのベット回数bに依存します。

なお論文中では先行研究より、\mu = -0.05, \sigma = 10.6で設定されています。

単一のベットの期待値\muがマイナスの値を取るのはギャンブルなので当たり前ですね。
なぜこのような仮定を置けるかというと、単一のベットに対するスロットマシーンの結果はランダムであるためです。つまりユーザーが十分に多い回数betし続けた場合、単一のbetの結果は期待値\muに収束します。
下のヒストグラムはそれぞれ、平均bet額の分布と合計bet回数の分布を表しています。


 結果ほとんどの平均bet額とbet回数の組み合わせのグループにおいて、正規性は棄却された。
ほとんどのグループで、正の歪度（positive skewness）を持つことが確認され、右側に歪んだ分布が存在することが確認された。
この結果は、ギャンブラーの離脱する際の総収支は正規分布に従わず、参照依存点や損失回避が作用し総収支がプラスのタイミングで離脱するギャンブラーが多いことを示す。


 実装例全てgoogle colabで動かしました。
Jarque-Bera Testの実装例コード
import numpy as np
from scipy.stats import jarque_bera
import matplotlib.pyplot as plt
import seaborn as sns


# 正規分布に基づくシミュレーションデータ（平均0, 標準偏差1）
normal_data = np.random.normal(0, 1, 1000)

# 左に歪んだシミュレーションデータ
skewed_data = np.concatenate([np.random.normal(0, 1, 900), np.random.normal(5, 1, 100)])

# Jarque-Bera検定の実行
jb_normal = jarque_bera(normal_data)
jb_skewed = jarque_bera(skewed_data)

jb_results = {
    "normal_data": {"JB statistic": jb_normal.statistic, "p-value": jb_normal.pvalue},
    "skewed_data": {"JB statistic": jb_skewed.statistic, "p-value": jb_skewed.pvalue},
}

for key, result in jb_results.items():
    jb = round(float(result['JB statistic']), 3)
    p = round(float(result['p-value']), 3)
    print(f"{key}: JB statistic = {jb}, p-value = {p}")
結果
正規分布のシミュレーションデータ

normal_data: JB statistic = 3.371, p-value = 0.185

→経験分布が正規分布に従うことを棄却できず。 p > 0.05
左に歪んだ分布のシミュレーションデータ

skewed_data: JB statistic = 583.167, p-value = 0.0

→経験分布が正規分布に従うことを棄却 p < 0.05
生成したデータの経験分布のヒストグラム
plt.style.use("ggplot")

# 可視化
fig, axs = plt.subplots(1, 2, figsize=(12, 5))

# 正規データのヒストグラム
sns.histplot(normal_data, kde=True, ax=axs[0], color="skyblue")
axs[0].set_title("Normal Data")
axs[0].set_xlabel("Value")
axs[0].set_ylabel("Frequency")

# 左に歪んだデータのヒストグラム
sns.histplot(skewed_data, kde=True, ax=axs[1], color="salmon")
axs[1].set_title("Skewed Data")
axs[1].set_xlabel("Value")
axs[1].set_ylabel("Frequency")

plt.tight_layout()
plt.show()

確かにJarque-Bera Testの結果通り、左のグラフのシミュレーションデータは正規分布に近いが、右のグラフのシミュレーションデータは左に偏りがあり正規分布とは離れていそうです。

 感想論文中ではおそらく触れられていなかったのだが、個人の平均bet額とbet回数によって、中止するタイミングの総収支が変動するメカニズムについても気になった。
より厳密で理想的な分析をするなら、個人の総資産に対するbet額の割合の情報もわかれば、元来その人がギャンブルに投ずる額によってもリスク愛好的かリスク回避的かどうかを判断できそう。
これからも誰も興味ないこと書くのでよかったらいいねください^^