Atcoder - ABC359 A - D まで復習解説

ABC359 A - D を復習してまとめてみました。初学者の方の参考になれば幸いです。

A - Count Takahashi

https://atcoder.jp/contests/abc359/tasks/abc359_a

問題文
文字列が $N$ 個与えられます。$i$ 番目 ($1 \le i \le N$) に与えられる文字列 $S_{i}$
​は Takahashi か Aoki のどちらかと等しいです。 $S_{i}$ が Takahashi と等しい
i がいくつあるか求めてください。

どこにあるかは関係なくいくつあるか求めるだけなので Python だと Counter を用いると楽です。
Counter の返り値は Dict like なオブジェクトなので get メソッドで値を取り出せますが Takahashi が１個もない場合は None が返ってくるので get("Takahashi", 0) としてデフォルト値を $0$ にしといてあげましょう。
入力例 2 がちょうど $0$ なのでそこで気づきやすいので優しいですね。

from collections import Counter

N = int(input())
S = [input() for _ in range(N)]
counts = Counter(S)
ans = counts.get("Takahashi", 0)
print(ans)

B - Couples

https://atcoder.jp/contests/abc359/tasks/abc359_a

２通りの解き方を紹介しておきます。

1. A[i] と A[i + 2] が等しいか調べる

公式解法の考え方です。「色 $i$ の服を着た二人の人の間にちょうど一人いるということ」と「$A[i]$ 番目と $A[i + 2]$ が等しい」 ということは同じと言え、後者のほうが調べるのが楽です。

そこで後者を調べるために前から for を回して「$A[i]$ 番目と $A[i + 2]$ が等しい」となる $i$ の数を数え上げましょう。

N = int(input())
A = list(map(int, input().split()))

ans = 0
for i in range(2 * N - 2):
    if A[i] == A[i + 2]:
        ans += 1
    
print(ans)

2. $i$ 色の服を着ている二人 に注目する方法

コンテスト中は 「「色 $i$ の服を着た二人の人の間にちょうど一人いるということ」を調べるコードを書いて AC しました。
正直公式解法のほうが楽ですがこういう書き方が役に立つこともあるかなと思うので紹介しておきます。

$2 \le N \le 100$ という制約から

$G[i] := 色 i の服を着た人が前から j 番目にいる情報を含むリスト$

と定義し $G[i][0] + 2 = G[i][1]$ である $i$ をカウントしました。

N = int(input())
A = list(map(int, input().split()))
G = [[] for _ in range(N + 1)]

for i, a in enumerate(A):
    G[a].append(i)

ans = 0
for g in G[1:]:
    if g[0] + 2 == g[1]:
        ans += 1

print(ans)

C - Tile Distance 2

https://atcoder.jp/contests/abc359/tasks/abc359_c

以前 Tile Distance という問題を解けなかったので少し苦手意識を持ってしまいましたが、怖がらずゆっくり読み解くことで AC することができました。

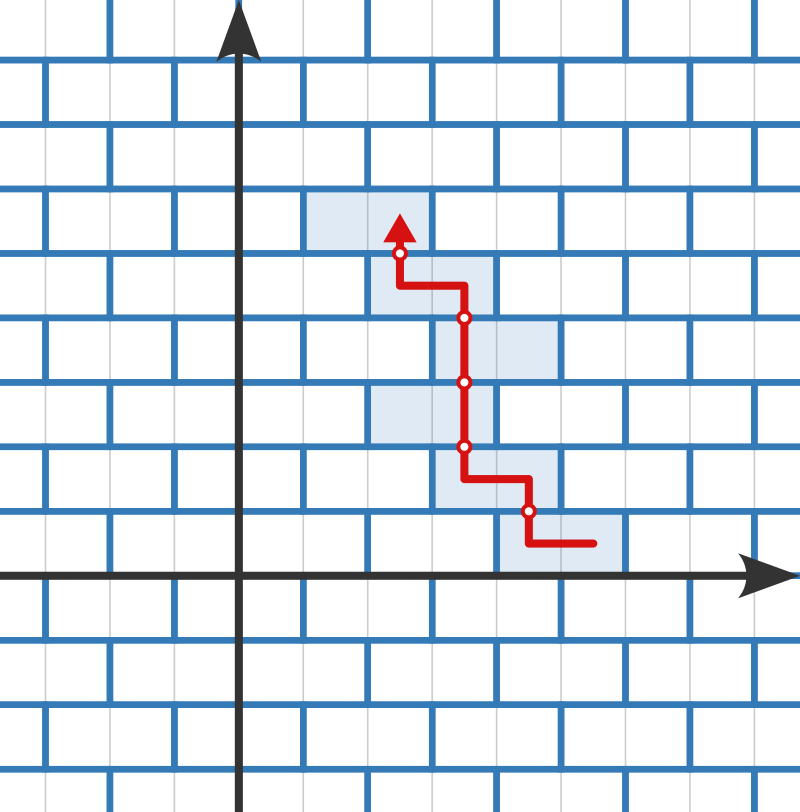
まず、出力例１の図をじっくり見てみました。

出典 ABC 359 C

思いついたことをまとめると以下のようになりました。

• $x$ 方向への移動と $y$ 方向への移動は非対称である
  • $x$ 方向は２マス進んでコスト１かかる
  • $y$ 方向は１マス進むごとにコスト１かかる
  • つまりそれぞれ独立に考えるということができない
• $y$ 方向へ移動した後に $x$ 方向へ１回ノーコストで移動できる
  • 画像だと１つ目と４つ目の赤丸の後にノーコストで左に移動している
  • １つ目と２つ目の赤丸の後に左に移動してても問題ない、できる限りさっさと左に移動したほうがよさそう

以上のことから

1. 先に $y$ 方向へ移動する
2. ついでに $x$ 方向へ１回ノーコストで移動する
3. 1, 2 をゴールと $y$ が一致するまで繰り返す
4. 最後に足りない分だけ $x$ 方向へコストをかけて移動する

という方針を立て実装しました。

スタートとゴールの位置関係は

1. スタートから見てゴールは右上にある
2. スタートから見てゴールは右下にある
3. スタートから見てゴールは左上にある
4. スタートから見てゴールは左下にある

の４パターンがありすべてを考えると複雑になってしまうので、スタートとゴールを入れ替えてもかかるコストは変わらなさそうということから

1. スタートから見てゴールは右上にある
2. スタートから見てゴールは右下にある
3. スタートから見てゴールは左上にある → スタートとゴールを入れ替えると 2 になる
4. スタートから見てゴールは左下にある → スタートとゴールを入れ替えると 1 になる

とすることから２パターンへ減らし、さらにスタートから見たゴールの $y$ 座標を上下反転しても同様にコストが変わらないことから

1. スタートから見てゴールは右上にある
2. スタートから見てゴールは右下にある → ゴールの $y$ 座標を上下反転して 1 になる

とし、１パターンのみの実装になります。
実装のパターンを減らしバグや考えることを減らすことはよく出てくるテクニックですね。
(とはいっても私はコンテスト中は２パターンまでにしか減らせませんでしたが)

１パターンのみ考えた実装例は以下のようになります。

sx, sy = map(int, input().split())
gx, gy = map(int, input().split())

if sx > gx:
    # 常にスタートが左側になるようにする
    sx, sy, gx, gy = gx, gy, sx, sy

if sy > gy:
    # 常にスタートが下側になるようにする
    gy = (gy - sy) * (-1) + sy

# 今いる 2x1 のタイルの左側にいるならノーコストで右側に移動する
if sy % 2 == sx % 2:
    # 左側にいる
    sx += 1

cost = 0

# 先に上に移動する。移動するたびノーコストで1マス右側に移動できる
dy = gy - sy
cost += dy
sx = min(sx + dy, gx)

# 右に移動する。コスト1で2マス進める
dx = gx - sx
cost += (dx + 1) // 2

print(cost)

D - Avoid K Palindrome

https://atcoder.jp/contests/abc359/tasks/abc359_d

コンテスト中は DP は DP でも区間 DP かなと難しく考えすぎて解くことができませんでした。解説を見た後に Upsolve しました。

前から $i$ 文字まで考えてそれがすでに 良い文字列 である時、その後ろに A, B のいずれかの文字をくっつけても同様に 良い文字列 であるかに関与しているのは今くっつけようとしている A, B と $i$ 文字の末尾 $K - 1$ 文字だけでそれより前の文字は考えなくていいです。

したがって私は区間 DP だと勘違いしてしまいましたが

$DP[i][S] := i 番目の文字列まで考え末尾が S である良い文字列の個数$

と定義し、前から順に DP をしていけばいいです。
(定義的にも間違ってないと思いますが、便宜上 $i < K$ の文字列はすべて良い文字列とみなしました)

最大である $K = 10$ の時でも $S$ の部分は A, B, AA, AB, ..., BBBBBBBBA, BBBBBBBBB となり多くて $2^{9} = 512$ 個しかないので、計算量は $O(N × 512)$ となり十分高速です。

S が文字列となるので DP は２次元リストで宣言されることが多いですが今回は defaultdict を用いたほうが実装が楽でした。

from collections import defaultdict


def is_palindrome(s: str) -> bool:
    return s == s[::-1]


N, K = map(int, input().split())
S = input()
MOD = 998244353

dp = defaultdict(int)
dp[""] = 1  # 空文字列をスタートとする

for i in range(N):
    if S[i] == "?":
        s = ["A", "B"]  # ? は A, B 両方のパターンを考える
    else:
        s = [S[i]]
    dp2 = defaultdict(int)
    for key, value in dp.items():
        for si in s:
            key2 = key + si
            if len(key2) == K and is_palindrome(key2):
                # 良い文字列ではないのでスキップ
                continue
            # K 文字の key2 を K - 1 文字だけにする
            key2 = key2[-(K - 1) :]
            dp2[key2] += value
            dp2[key2] %= MOD
    dp = dp2

ans = 0
for value in dp.values():
    ans += value
    ans %= MOD
print(ans)