Atcoder - ABC343 A - F まで復習解説

ABC343 A - F を復習してまとめてみました。初学者の方の参考になれば幸いです。

A - Wrong Answer

https://atcoder.jp/contests/abc343/tasks/abc343_a

問題文
$0$ 以上 $9$ 以下の整数 $A$,$B$ が与えられます。
$0$ 以上 $9$ 以下の整数であって $A+B$ と等しくないものをいずれかひとつ出力してください。

for で $0$ から $10$ までループを回し、 $A + B$ でないものを見つけたら出力しました。

A, B = map(int, input().split())

for i in range(0, 10):
    if i != A + B:
        print(i)
        exit()

B - Adjacency Matrix

https://atcoder.jp/contests/abc343/tasks/abc343_b

グラフ構造を保存する２つのデータ構造として、隣接行列 (英語だと Adjacency Matrix (問題のタイトル))、２次元リストがあります。
隣接行列で与えられているグラフ構造を２次元リスト表記しなさいという問題です。
ただ、データとして保持する必要がないのでもっというと２次元やリストにする必要は必ずしもないです。(今回は簡便さからリストにはしています)

２回の for ループで $i$ 行目の $j$ 番目の要素が $1$ なら頂点 $i$ が頂点 $j$ と辺で結ばれていると言えるので $i$ ごとに $j$ 番目が $1$ なら $j$ をリストに append していきましょう。
最後に print すればOKです。Python ではリストは print(*ret) というようにすると期待されている出力ができるので楽です。

N = int(input())
A = [list(map(int, input().split())) for _ in range(N)]
for i, a in enumerate(A, 1):
    ret = []
    for j, aa in enumerate(a, 1):
        if aa == 1:
            ret.append(j)
    print(*ret)

C - 343

https://atcoder.jp/contests/abc343/tasks/abc343_c

• $343 = 7^{3}$ のようにある値の３乗である値
• 左から読んでも右から読んでも同じいわゆる回文となっている値

を回文立方数と定義し、 $N$ 以下で最も大きい回文立方数を探します。
(ちなみに $343$ が何の３乗か最初わからなくて手元でちょこちょこ計算して求めました)

$1 \le N \le 10^{18}$ と非常に大きくて全探索は無理のように見えますが、ややメタ的な発言になりますがこういうときは実は $10^{6}$ 程度まで考えればいいということが多いです。

今回の場合もそうで、 $x^{3} = K$ より $x$ と $K$ は一対一対応であり (つまり複数の $x$ の値が同じ $K$ になることはない)、 そうであれば

• ３乗しても $N$ 以下である
• ３乗した値は回文となっている

という $x$ を探すと問題を言い換えてみると、 $1 \le N \le 10^{18}$ より例えば $x = 10^{7}$ は３乗すると $10^{21}$ より必ず $N$ より大きくなるので、 $x$ は必ず $1 \le x \le 10^{6}$ という制約に収まります。

$1 \le x \le 10^{6}$ であれば全探索しても間に合いますので、全探索をしましょう。
$1 \le x \le 10^{6}$ である時点で１つ目の条件である「３乗しても $N$ 以下である」は満たしますので、もう一つの「３乗した値は回文となっている」かどうかを判定して最も大きい値を出力しましょう。

回分かどうかは文字列として扱い反転した値と等しいかどうかで判断すると楽だと思います。

N = int(input())
M = 10**6 + 10

def is_ok(x: int):
    # x の３乗が回文立方数であるかどうかを判定する
    K = x * x * x
    L = str(K)
    if L == L[::-1]:
        return True

ans = 0
for i in range(M):
    if i * i * i > N:
        break
    if is_ok(i):
        ans = max(ans, i)

print(ans ** 3)

D - Diversity of Scores

https://atcoder.jp/contests/abc343/tasks/abc343_d

状況が変化する事にある値がどう変化するかを聞いている問題です。実際にシミュレーションしてみましょう。

ただし

for _ in range(T):
    a, b = map(int, input().split())
    A[a] += b
    print(len(set(A)))

というように毎回 $A$ の要素を前から走査し種類の個数を確認していると全体で計算量が $O(T×N)$ で TLE となってしまいますので工夫が必要です。

「得点が何種類あるか」が変化するところを考えてみると

• 得点 $x$ が今まで存在していなくて、新たに存在するようになった
• 得点 $x$ が今まで存在していたが、存在しなくなった

のいずれのときのみ「得点が何種類あるか」が変化します。

そこで

• $scores[i] := 選手 i の得点$
• $counts[i] := 得点 i である選手の数$ を保存する defaultdict
• 「得点が何種類あるか」を保存する num_types

を用意しておくと上記の２つは

• 得点 $x$ が今まで存在していなくて、新たに存在するようになった： counts[x] が $0$ から $1$ になったら num_types を $1$ 増やす
• 得点 $x$ が今まで存在していたが、存在しなくなった： counts[x] が $1$ から $0$ になったら num_types を $1$ 減らす

と言い換えることができます。計算量は $O(T)$ です。あるイベントが生じる時は全体の中でわずかな時しかないのに気づくのがこのような問題では大事です。

N, T = map(int, input().split())

scores = [0] * N
counts = defaultdict(int)
counts[0] = N  # はじめは N 人 0 点である
num_types = 1  # はじめは 0 のみ

for _ in range(T):
    a, b = map(int, input().split())
    a -= 1

    current_score = scores[a]
    new_score = current_score + b

    counts[new_score] += 1
    if counts[new_score] == 1:
        # 新しいスコアの種類が増えた
        num_types += 1

    counts[current_score] -= 1
    if counts[current_score] == 0:
        # スコアの種類が一つ減った
        num_types -= 1

    # a のスコアを更新
    scores[a] = new_score

    print(num_types)

E - 7x7x7

https://atcoder.jp/contests/abc343/tasks/abc343_e

まず状況を絞り込むことを考えると $V1$, $V2$, $V3$ を満たすような立方体が存在し、それが離れて空間に置かれている時、それぞれを接するように移動させても問題がないはずです。(重なるようにしたら $V1$, $V2$, $V3$ が変化しますが重なっていない体積は変化していないので)

したがって

• 「重ならない場合は必ず接している」 $V1$, $V2$, $V3$ を探索する
• さらに $C1$ の端の座標の1つを $(a1, b2, c3) = (0, 0, 0)$ と置く

と問題を置き換えても求めたい答えを見つけることができるので以降そうします。

そうすると「重ならない場合は必ず接している」という条件より $(0, 0, 0)$ に接するように置くためには各座標 $a2$, $b2$, $c2$, $a3$, $b3$, $c3$ は $-7$ 以上 $7$ 以下の範囲に存在している必要が出てき、その範囲は 0 も含めて 15 なので $15 × 15 × 15 × 15 × 15 × 15 = 15^{6} = 11,390,625$ となり全探索しても間に合いそうな計算量になります。

よってすべての座標を全探索しちゃいましょう。

ただし、各探索で行う１つ１つの計算が非常に重いため、実は PyPy でも TLE になってしまいます。私はコンテスト中に AC することはできなかったのですが、もしコンテスト中に Python で実装していたら ChatGPT を使うなどして C++ に実装し直したかなと思います。

公式解説を読むと、実は探索する範囲を $-1$ 以上 $7$ 以下の範囲にさらにしぼっても探索が可能だそうなので、今回の以降の実装ではそちらに範囲をさらにしぼっておきます。これなら Python でも２秒以内に計算できます。
(ただし、コンテスト中にこの範囲にしぼってもいいということに気づけるのはかなり難しいかなと思います)

話を戻します。

まず、話を簡単にするために「大きさ７の２次元の四角形２つ $(a1, b1)$, $(a2, b2)$ の重なっている面積を求める」場合を考えると以下のように幅は $a1$, $a2$ の小さい方に７足したものから大きい方の値を引くと求めることができます。
(この考えは「最低でも接している」という条件がないと使えないため最初にそのような条件を入れています)

ただし、後で３つあるときを考えると以下のような図のような場合は負になってしまうことがあるため、そのような場合は 0 とみなすために最終的には

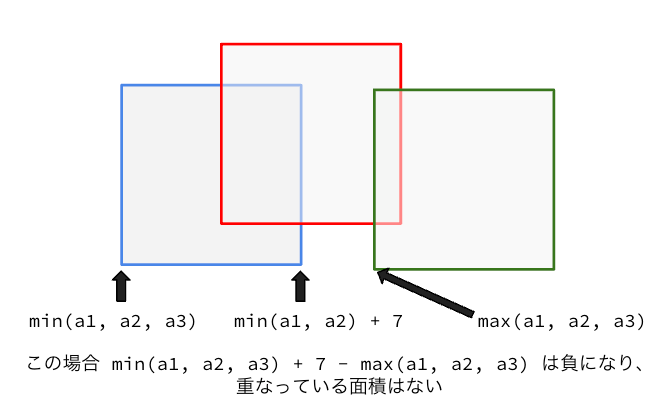
x = max(min(a1, a2) + 7 - max(a1, a2), 0)

という式で表すことができます。高さも $b1$, $b2$ に対して同じように計算すれば求められるので
「大きさ７の２次元の四角形２つ $(a1, b1)$, $(a2, b2)$ の重なっている面積を求める」関数は以下のようになります。

def calculate_square(position1, position2):
    a1, b1 = position1
    a2, b2 = position2
    x = max(min(a1, a2) + 7 - max(a1, a2), 0)
    y = max(min(b1, b2) + 7 - max(b1, b2), 0)
    return x * y

３次元に拡張したり、３点の重なる面積 (体積) 場合も考え方は同じなので、例えば「大きさ７の３次元の立方体３つ $(a1, b1, c3)$, $(a2, b2, c3)$, $(a3, b3, c3)$ の重なっている体積を求める」関数は以下のようになります。

def calculate_volume(position1, position2, position3):
    a1, b1, c1 = position1
    a2, b2, c2 = position2
    a3, b3, c3 = position3
    x = max(min(a1, a2, a3) + 7 - max(a1, a2, a3), 0)
    y = max(min(b1, b2, b3) + 7 - max(b1, b2, b3), 0)
    z = max(min(c1, c2, c3) + 7 - max(c1, c2, c3), 0)
    return x * y * z

なお実際の実装中では以下のように１つ、２つ、３つの立方体のいずれの重なった場合でも対応できるように for 文を使って実装しました。

def calculate_volume(positions) -> int:
    x = max(0, min(p[0] for p in positions) + 7 - max(p[0] for p in positions))
    y = max(0, min(p[1] for p in positions) + 7 - max(p[1] for p in positions))
    z = max(0, min(p[2] for p in positions) + 7 - max(p[2] for p in positions))
    return x * y * z

以上のようにして重なっている堆積を求める関数が実装できたのであらためて全探索の各探索で計算する必要があるものを考えると、３つの立方体の座標が決まっている状況で

• ３つの立方体が重なっている体積
• ２つの立方体が重なっている体積
• １つの立方体が重なっている体積 (１つの立方体のみ存在している体積)

をヌケモレなく計算する必要があります。これは包除原理を用いるとよいです。

https://ja.wikipedia.org/wiki/包除原理

３つの体積の重なりは以下のベン図で表すことができます。

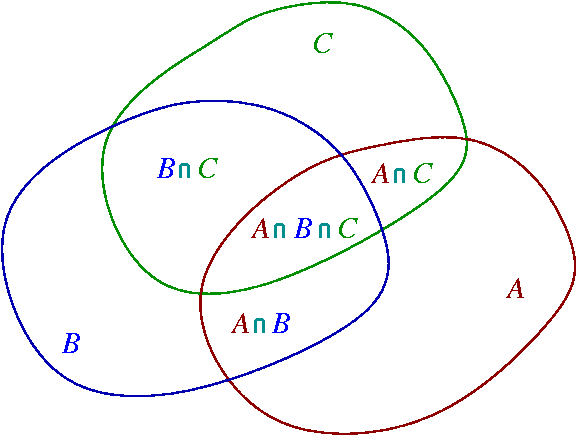
Wiki より

以上のことよりヌケモレなく計算すると

「３つの立方体が重なっている体積」 = calculate_volumne($C_{1}$, $C_{2}$, $C_{3}$)

「２つの立方体が重なっている体積」は caluculate_volume では「３つの立方体が重なっている体積」を余分に計算してしまうので多い分を引き算します。

「２つの立方体が重なっている体積」 = calculate_volumne($C_{1}$, $C_{2}$) + calculate_volumne($C_{2}$, $C_{3}$) + calculate_volumne($C_{3}$, $C_{1}$) - 3 ×「３つの立方体が重なっている体積」

「１つの立方体が重なっている体積」の場合は全て重なっていない場合は $3 × 7 × 7 × 7$ なのでそこからも同様に考えて余分な部分を引き算します。

「１つの立方体が重なっている体積」 = $3 × 7 × 7 × 7$ - 「２つの立方体が重なっている体積」 × 2 - 「３つの立方体が重なっている体積」 × 3

計算したそれぞれが $V3$, $V2$, $V1$ と等しければその座標を表示して計算をやめます。全探索しても見つからなければ $No$ を表示して終了します。

def calculate_volume(positions):
    x = max(0, min(p[0] for p in positions) + 7 - max(p[0] for p in positions))
    y = max(0, min(p[1] for p in positions) + 7 - max(p[1] for p in positions))
    z = max(0, min(p[2] for p in positions) + 7 - max(p[2] for p in positions))
    return x * y * z


V1, V2, V3 = map(int, input().split())

x1 = 0
y1 = 0
z1 = 0
position1 = [x1, y1, z1]
S = 7

for position2 in product(range(-1, S + 1), repeat=3):
    # position2 = (x2, y2, z2)
    for position3 in product(range(-1, S + 1), repeat=3):
        # position3 = (x3, y3, z3)

        # 3つ重なっているところが V3 と一致しているか
        volume_123 = calculate_volume((position1, position2, position3))

        overlapped_volume3 = volume_123

        if overlapped_volume3 != V3:
            continue

        # 2つ重なっているところが V2 と一致しているか
        volume_12 = calculate_volume((position1, position2))
        volume_23 = calculate_volume((position2, position3))
        volume_31 = calculate_volume((position3, position1))

        # 多く計算している部分を引きつつ重なっている立方体が2つだけの部位の体積を求める
        overlapped_volume2 = volume_12 + volume_23 + volume_31 - overlapped_volume3 * 3
        if overlapped_volume2 != V2:
            continue

        # 1つ重なっているところが V1 と一致しているか
        volume_1 = calculate_volume((position1,))
        volume_2 = calculate_volume((position2,))
        volume_3 = calculate_volume((position3,))

        # 多く計算している部分を引きつつ重なっている立方体が1つだけの部位の体積を求める
        overlapped_volume1 = 3 * 7 * 7 * 7 - overlapped_volume2 * 2 - overlapped_volume3 * 3
        if overlapped_volume1 != V1:
            continue

        ans = list(position1) + list(position2) + list(position3)
        print("Yes")
        print(*ans)
        exit()

print("No")

F - Second Largest Query

https://atcoder.jp/contests/abc343/tasks/abc343_f

上から２番目の値を走査し調べる必要がある問題です。一点更新、区間で走査するクエリが何度も行う必要があるので max などならすぐ SegTree かなと思ったのですが「２番目に大きい値ってどうやって保存するんだろ？」、「 max の値は SegTree で調べて、そこからうまく次に大きい値を取り出す？」などと考え込んでしまいました。

色々ググったりした結果、 SegTree で保持する値は必ずしも１つに限らなくてよいので、$(区間で最大の値、２番目に大きい値)$ を要素として保持する SegTree を実装すればよいと気づきました。 (SegTree は奥が深いですね。おもしろい)

$(区間で最大の値、２番目に大きい値)$　を取り出せるようになったら、次はその２番目に大きい値が同じ区間に何個含まれているかを調べる必要があります。

こちらも BIT などのデータ構造を使えばいいのかなとあれこれ悩みましたがコンテスト残り20分ぐらいになって $(区間で最大の値、２番目に大きい値)$ と2つの値を保持するのであればひらきなおって $(区間で最大の値、２番目に大きい値、最大の値の数、2番目に大きい値の数)$ と４つの値を保持すればいいんじゃないかと気づきました。

この時、単位元 $e$ は $e = (0, 0, 0, 0)$ となります。 $1 \le A_{i} \le 10^{9}$ という制約からタイプ $1$ のクエリの更新によって $A_{i}$ が $0$ になることはないのでちょうどいいです。

$op$ は２つのノードを $a$, $b$ とすると「 $a$ の最大の値」、「 $a$ の２番目の値」、「 $b$ の最大の値」、「 $b$ の２番目の値」の４つの数字から新しい $(区間で最大の値、２番目に大きい値、最大の値の数、2番目に大きい値の数)$ を求める必要があり若干計算量が大きめになってしまいます。

def op(node1, node2):
    # node1 と node2 の最大値と2番目に大きい値をマージ
    values = sorted(set([node1[0], node1[1], node2[0], node2[1]]), reverse=True)
    # 値が１つしかない場合
    if len(values) == 1:
        return (values[0], -INF, node1[2] + node2[2], 0)
    # 最大の2つの値を取得
    max_val = values[0]
    max_val_count = 0
    if node1[0] == max_val:
        max_val_count += node1[2]
    if node1[1] == max_val:
        max_val_count += node1[3]
    if node2[0] == max_val:
        max_val_count += node2[2]
    if node2[1] == max_val:
        max_val_count += node2[3]
    second_max_val = values[1]
    second_max_val_count = 0
    if node1[0] == second_max_val:
        second_max_val_count += node1[2]
    if node1[1] == second_max_val:
        second_max_val_count += node1[3]
    if node2[0] == second_max_val:
        second_max_val_count += node2[2]
    if node2[1] == second_max_val:
        second_max_val_count += node2[3]
    return (max_val, second_max_val, max_val_count, second_max_val_count)

しかし、上記のコンテスト中に実装した $op$ では計算量が大きいため TLE になってしまい AC することができませんでした。

そしてコンテスト後 ChatGPT を用いて C++ に実装したものや if else の条件分岐をしっかり書き無駄な計算をしないようにアップデートした $op$ の Python で AC することができました。
(あとちょっとで F 問題正解がかかってただけに悔しいですが、次回こそ頑張りたいです)

from atcoder.segtree import SegTree

N, Q = map(int, input().split())
A = list(map(int, input().split()))

# 前から最大値と二番目に大きい値とそれぞれの個数を持つ
e = (0, 0, 0, 0)

def op(a, b):
    a1, a2, a3, a4 = a
    b1, b2, b3, b4 = b
    if a1 == b1:
        if a2 == b2:
            return (a1, a2, a3 + b3, a4 + b4)
        elif a2 > b2:
            return (a1, a2, a3 + b3, a4)
        else:
            return (a1, b2, a3 + b3, b4)
    elif a1 > b1:
        if a2 == b1:
            return (a1, a2, a3, a4 + b3)
        elif a2 > b1:
            return (a1, a2, a3, a4)
        else:
            return (a1, b1, a3, b3)
    else:
        if b2 == a1:
            return (b1, b2, b3, a3 + b4)
        elif b2 > a1:
            return (b1, b2, b3, b4)
        else:
            return (b1, a1, b3, a3)


segtree = SegTree(op, e, [(a, 0, 1, 0) for a in A])

for _ in range(Q):
    query = list(map(int, input().split()))
    if query[0] == 1:
        _, p, x = query
        p -= 1
        segtree.set(p, (x, 0, 1, 0))
    else:
        _, l, r = query
        l -= 1
        *_, second_val_count = segtree.prod(l, r)
        print(second_val_count)