日本に四季は存在するのか?気温データで検証してみた!
はじめに
こちら記事の前章になります。
日本は四季がはっきりしていることが魅力といわれておりますが、最近は温暖化の影響で季節感が薄れている気がしませんか?(体感的には夏と冬めっちゃ長い)
そこで、本記事では気温データを使って統計的に日本に四季が存在するのか検証していきたいと思います。
結論:日本に四季は存在する
結論から言うと、日本に四季は存在しました。
日本に四季は存在したのか?
では検証していきましょう!
データは福島県福島市の気温を使用しました。理由は「四季の里」なる施設があったためです。きっと福島市は四季がはっきりしているのでしょう(名推理)。福島県民の方、本当かどうかよかったらコメントください。
検証方法
STEP1.一元配置分散分析(ANOVA)
各季節の真ん中月である1月、4月、7月、10月が他の月と異なる気温群であることを検証します。
「4つの気温が異なるか?」をチェックします。ANOVAでは、どの季節が異なるか?までは検証できません。
STEP2.テューキー検定(Tukey検定)
各月をそれぞれ比較し、異なる気温群であることを検証します。
例えば「春と夏は異なるか?」や「夏と秋は異なるか?」など具体的にどの季節がどの季節と異なるのかを求めます。
STEP3.箱ひげ図
箱ひげ図を用いて、各月の気温群を可視化します。グラフにすることで視覚的に考察することができます。
STEP1.ANOVA
ANOVAとは
ANOVAは3つ以上のグループの平均の差を分析する統計手法です。今回は因子の数が「気温」の一つのため、一元配置分散分析(One-Way ANOVA) を用います。
ANOVA仮説
-
帰無仮説
- 1月の気温平均=4月の気温平均=7月の気温平均=10月の気温平均
-
対立仮説
- 1月の気温平均、4月の気温平均、7月の気温平均、10月の気温平均の中に異なる値がある
p値<0.05でどこかの季節の気温平均に差があることが有意とわかります。
仮説が有意になれば「春と夏と秋と冬のどれかは違う季節ですね〜」ということがわかります。例えば「春と夏は違いますよ〜」というように、どのグループがどのグループと差異があるかはわかりません。
気温の元データを気象庁ホームページから取得
気象庁より、次のデータをダウンロードしました。
- 場所:福島県福島市
- 項目:月平均気温
- 期間:2019年〜2023年(5年分)
- オプション:
- 利用上注意が必要なデータは格納しない
- 観測環境などの変化にかかわらず、すべての期間の値を表示(格納)する。ただしデータの不均質を示す情報をつける。
コード
一元配置分散分析を実行するコードは以下になります。
import pandas as pd
import numpy as np
from scipy import stats
df = pd.read_csv('./data/hukushima.csv', encoding='shift-jis', header=[3])
# データ形式を整備
df = df.drop(0)
df = df.drop(['平均気温(℃).1'], axis=1)
df["月"] = df["月"].astype('int')
df["年"] = df["年"].astype('int')
# 1月,4月,7月,10月のデータを抽出
target_months = [1,4,7,10]
seasonal_data = df[df['月'].isin(target_months)]
# 月ごとの気温データを配列に格納
groups = []
for month, month_group in seasonal_data.groupby('月'):
temperatures = month_group['平均気温(℃)'].values
groups.append(temperatures)
# 一元配置分散分析の実行
f_value,p_value = stats.f_oneway(*groups)
print("\n=== 一元配置分散分析の結果 ===")
print(f"分析対象月: 1月, 4月, 7月, 10月")
print(f"F値: {f_value:.4f}")
print(f"p値: {p_value:.4f}")
print(f"有意水準0.05で有意差{'' if p_value < 0.05 else 'なし'}")
# 一元配置分散分析の実行
f_value,p_value = stats.f_oneway(*groups)
groupsには1月,4月,7月,10月の気温配列が入っています。右辺のf_valuegがf値、p_valueがp値になります。
f値とp値の意味
f値
f値はグループ間の分散とグループ内の分散を比較する統計量です。値が大きいほどグループ間に大きな差があることを示します。
グループ内分散はグループの中でどれだけ分散が大きいかを表します。今回だと、各月の中での平均のばらつきを示します。

グループ間分散はグループと全体の平均の差の大きさを表します。今回だと、各月の平均気温と全体の平均との差がどれだけあるかを示します。

p値
p値は、帰無仮説を考えた時、得られた結果が偶然である確率を示します。
ちなみにp値の「P」はProbability(確率)という意味です。
p値 < 0.05の場合、統計的に有意な差があると言われています。これは、平均値から±標準偏差2個分に含まれるデータは全体の約95%を占めるという標準偏差の95%ルールから来ています。
要するに5%以下だったら滅多に起きないよね〜、違うことが偶然じゃないよね〜という意味です。
結果
結果はp値が0.0000であり、p値 < 0.05になりました。(超有意な結果ですね笑)
よって、対立仮説「1月の気温平均、4月の気温平均、7月の気温平均、10月の気温平均の中に異なる値がある」は有意になります。

STEP2.Tukey検定
Tukey検定
Tukey検定は多重比較法の一つです。各グループをそれぞれ比較する検定方法です。ANOVAではグループのどれかが異なることを検定しましたが、Tukey検定はどのグループがどのグループと異なるかをすべて比較することができます。
コード
Tukey検定を実行するコードは次になります。
from statsmodels.stats.multicomp import pairwise_tukeyhsd
# データを多重比較用に整形
months = np.repeat(target_months, [len(group) for group in groups])
values = np.concatenate(groups)
# Tukey's HSDの実行
tukey = pairwise_tukeyhsd(values, months)
print("\n=== Tukey's HSD(多重比較)===")
print(tukey)
Tukey検定を実行する関数はpairwise_tukeyhsd()です。使い方はhelp関数より確認することができます。第一引数endogはendogenous variable(内生変数)の略でグループの対象を示す値です。今回だと月ごとの気温が二次元配列に格納されます。
help(pairwise_tukeyhsd)
===========================================================================
Help on function pairwise_tukeyhsd in module statsmodels.stats.multicomp:
pairwise_tukeyhsd(endog, groups, alpha=0.05)
Calculate all pairwise comparisons with TukeyHSD confidence intervals
Parameters
----------
endog : ndarray, float, 1d
response variable
groups : ndarray, 1d
array with groups, can be string or integers
alpha : float
significance level for the test
Returns
-------
results : TukeyHSDResults instance
A results class containing relevant data and some post-hoc
calculations, including adjusted p-value
Notes
-----
This is just a wrapper around tukeyhsd method of MultiComparison
See Also
--------
MultiComparison
tukeyhsd
statsmodels.sandbox.stats.multicomp.TukeyHSDResults
結果
pairwise_tukeyhsd関数の実行結果を見るとrejectがすべてtrueとなっています。これより、1月,4月,7月,10月の気温群に有意な差があることがわかりました。

よって、気温という項目からみると、日本に四季が存在することがわかりました。
STEP3.箱ひげ図よりデータを可視化
STEP2.より数値的に季節間に差異があることは確認できました。しかし、いまいちピンとこない方も多いかと思います。そこで、箱ひげ図を使って各季節の気温の分散を可視化したいと思います。
箱ひげ図の見方
箱ひげ図はデータの分布を可視化するグラフです。
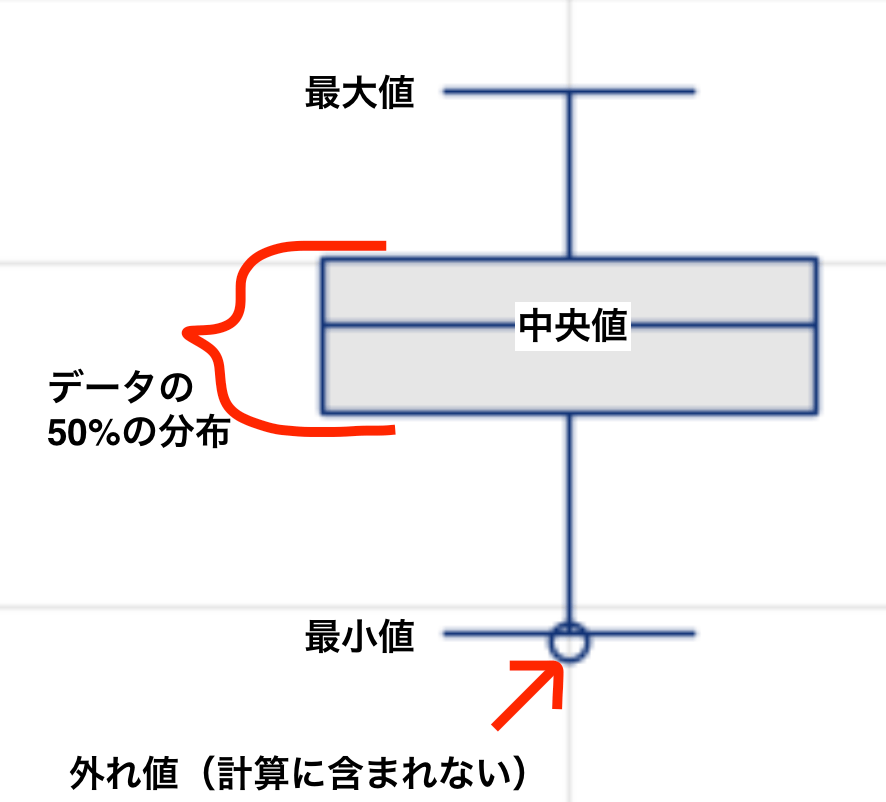
コード
# プロットのスタイル設定
plt.figure(figsize=(6, 6))
# 箱ヒゲ図の作成
sns.boxplot(data=seasonal_data, x='月', y='平均気温(℃)',width=0.4,color=".9", linecolor="#137" )
plt.title('月別の気温分布', pad=15, fontsize=14, fontweight='bold')
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
結果
各月の気温群の分布になります。可視化するとよくわかりますが、気温の分布が被っている季節はありません。

また、各月の気温の中央値は次の結果になりました。
| 月 | 気温 (℃) |
|---|---|
| 1(冬) | 1.9 |
| 4(春) | 12.2 |
| 7(夏) | 25.2 |
| 10(秋) | 15.7 |
- 最も気温差が大きい季節の変化:秋→冬(Δ13.8℃)
- 最も気温差が小さい季節の変化:夏→秋(Δ9.5℃)
おわりに
日本の四季は健在!やったね!
参考リンク
How to Perform ANOVA in Python



Discussion