10分で今からでもVAE入門
前提
以下の前提を満たしていれば10分でVAEに関して理解できると思います!
- AutoEncoderに関して理解していること
- 誤差逆伝播法に関して理解していること(そんなにわかってなくてもいいかも)
- 実装を動かすことは10分のカウントに入れないこと!
はじめに
ざっくり流れだけ話すと
Step1. アーキテクチャが似てるAEとVAEをまず比較します。なぜVAEだと生成がうまくいくのかを解説します。
Step2. VAEはどんな損失関数を下げるように学習するのかを解説します。数式は避けて、直感的に損失関数を下げることは何を意味するのか?を解説するように心がけました!
Step3. Pytorchでどう実装するのか?です。結果に関してはほんのちょっとだけですが、載せました。
Step1. オートエンコーダーとVAEの違い
オートエンコーダー(AE)と変分オートエンコーダー(VAE)はかなりアーキテクチャが似ています。
似ているのでAEでも十分なんじゃない?と思ってしまうほどです。
まずはなぜ変分オートエンコーダーがうまく生成できるようになったのか?をAEとVAEを比較してみていきたいと思います。
オートエンコーダー(AE)
オートエンコーダーは、入力データを圧縮(エンコード)し、その圧縮された表現から元のデータを再構成(デコード)することを目的としたニューラルネットワークです。AEは通常、2つの部分から成り立っています。
- エンコーダー:入力データを低次元の潜在変数に変換します。
- デコーダー:その潜在変数から元のデータを再構成します。
AEの損失関数は、再構成されたデータと元のデータの差(例えば、二乗誤差)を最小化することです。

なぜAEではダメか?
AEのデコーダーは、学習した潜在ベクトル周辺のデータが入力されることを想定して学習されます。
つまり、潜在空間内のデータがデコーダーに入力されると、デコーダーはその周辺のデータを再構成し、元の訓練データに近いものを生成します。
一方、潜在ベクトル周辺から外れたデータでは再構成されたデータの品質が低下する可能性があります。
AEでは、特定のデータポイントに対して特定の潜在変数を学習します。そのため、デコーダーは学習した潜在ベクトル周辺のデータが入力されることを前提に学習されているので、潜在空間の未学習領域からサンプリングされたデータを入力すると、生成するデータの品質が低下してしまいます。
イメージこんな感じ

変分オートエンコーダー(VAE)
VAEはAEで持っていた問題を克服しています。以下がアーキテクチャです

VAEではなぜうまくいくのか?
AEとほとんど変わらないレイヤー構造で、違うのは潜在変数がどう構成されるかだけです。
AEはデータポイントごとの学習だったので学習された潜在変数空間が連続でない可能性がありました。
しかし、VAEはデータの潜在変数を確率分布としてモデル化することで、潜在変数空間をなめらか(連続的)にしているのです。
潜在変数の分布は標準正規分布に近づくように学習していきます。

こうすることで、潜在空間全体がうまく活用され、どこからサンプリングしても意味のあるデータが生成されやすくなります。
Step2. VAEの学習
VAEとAEの違いがわかったところで、次に学習するためにどんな損失関数を下げるかをみていきましょう。
VAEとAEの違いがわかると損失関数も理解しやすくなります。
AEの損失関数は単に、入力を出力を回答、入力を正解として出力で入力を再構成できるように再構成誤差を減らすようにしていました。
VAEはそれに加えて、潜在空間を標準正規分布にするという制約を入れるだけです!
VAEの損失関数の意味
いろんな解説を見るとELBOがどうとかと出てきますが、結局やりたいことは
- AEと同じで出力を回答、入力を正解として出力で入力を再構成できるように再構成誤差を減らす
- 潜在変数の分布が、標準正規分布になるように、エンコーダーの出力から構築する分布と標準正規分布が近づくようにKLダイバージェンスを減らす

つまり、損失関数は以下のようになります!
この損失関数を下げていけば、学習できます。
ここで押さえておいて欲しいのは、KLダイバージェンス と 再構成誤差では値がトレードオフになってい流ということです。
例えば、KLダイバージェンスを下げていこうとすると、潜在変数が標準正規分布に近づいていき分布として一般化されていきます。そうなると、特化した学習ではないので、再構成誤差は上がる可能性があります。
逆に再構成誤差を下げていこうとするとその逆で、再構成に特化しすぎて潜在変数の分布がそれように特化してしまいます。
つまり何が言いたいかというと、VAEはAEを汎化させたものであるということです。
実際に学習させるにはもう一工夫
サンプリングすると微分できないからうまく学習できない。
期待値と分散から正規分布を作ったとして、潜在変数をそこからサンプリングして取得してデコーダに流すとします。
そうすると学習の際に問題が発生します。
サンプリングがあると微分できないので、誤差逆伝播できないのです!
ここで誤差逆伝播法を使う前提で話していますが、使わない場合も同様に微分は行うはずなので結局は同じです。まあ誤差逆伝播法を使わないことはないと思いますが...

Reparametrization Trick(再パラメータ化トリック)で微分可能にして学習できるように!
この問題を解決するために具体的には、潜在変数z を次のように表現します。
これは、期待値
これはReparametrization Trick(再パラメータ化トリック)という呼ばれています。

これを使うことでStep1で表示したVAEのアーキテクチャになります。
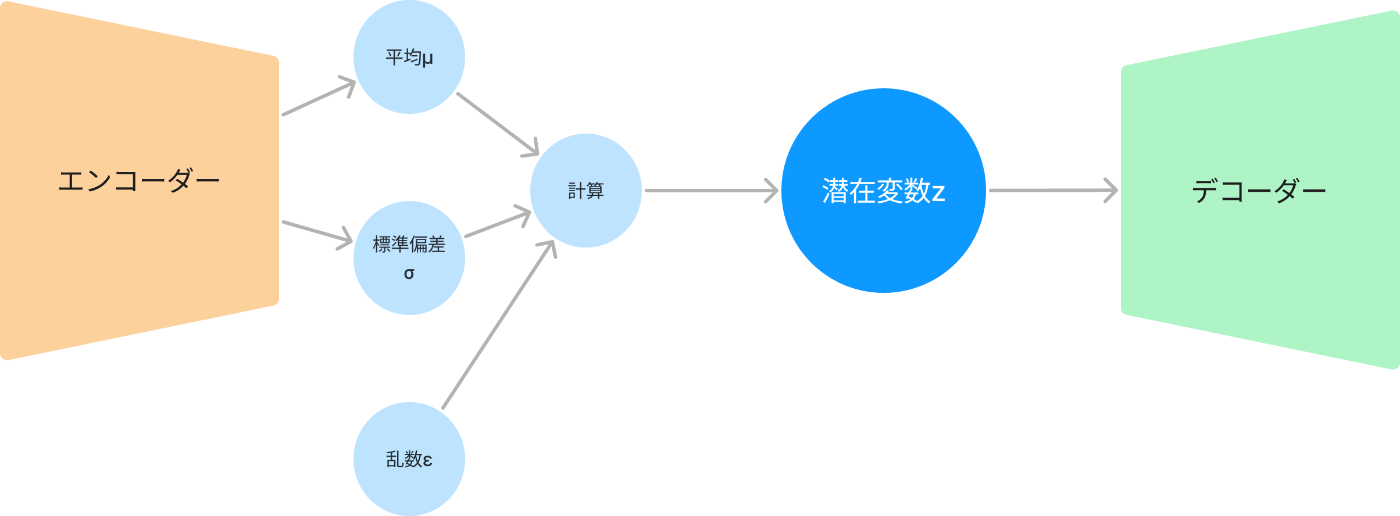
これでVAEが学習できるようになりました!
Step3. 実装
では実装に入りましょう!
まずはpytorchをインストール
!pip install torch
そして、以下を実行すると学習が始まります。
import torch
from torch import nn, optim
from torch.nn import functional as F
from torch.utils.data import DataLoader
from torchvision import datasets, transforms
from torchvision.utils import save_image
import os
class VAE(nn.Module):
def __init__(self):
super(VAE, self).__init__()
self.fc1 = nn.Linear(784, 400)
self.fc21 = nn.Linear(400, 20) # mu
self.fc22 = nn.Linear(400, 20) # logvar
self.fc3 = nn.Linear(20, 400)
self.fc4 = nn.Linear(400, 784)
def encode(self, x):
h1 = F.relu(self.fc1(x))
return self.fc21(h1), self.fc22(h1)
def reparameterize(self, mu, logvar):
std = torch.exp(0.5 * logvar)
eps = torch.randn_like(std)
return mu + eps * std
def decode(self, z):
h3 = F.relu(self.fc3(z))
return torch.sigmoid(self.fc4(h3))
def forward(self, x):
mu, logvar = self.encode(x.view(-1, 784))
z = self.reparameterize(mu, logvar)
return self.decode(z), mu, logvar
# デバイスの設定
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
print(device)
# データローダーの準備
train_loader = DataLoader(
datasets.MNIST('../data', train=True, download=True,
transform=transforms.ToTensor()),
batch_size=128, shuffle=True)
# モデルとオプティマイザーの設定
model = VAE().to(device)
optimizer = optim.Adam(model.parameters(), lr=1e-3)
def train(epoch):
model.train()
train_loss = 0
for batch_idx, (data, _) in enumerate(train_loader):
data = data.to(device)
optimizer.zero_grad()
recon_batch, mu, logvar = model(data)
loss = loss_function(recon_batch, data, mu, logvar)
loss.backward()
train_loss += loss.item()
optimizer.step()
if batch_idx % 10 == 0:
print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
epoch, batch_idx * len(data), len(train_loader.dataset),
100. * batch_idx / len(train_loader),
loss.item() / len(data)))
print('====> Epoch: {} Average loss: {:.4f}'.format(
epoch, train_loss / len(train_loader.dataset)))
# 訓練の実行
for epoch in range(1, 20):
train(epoch)
if not os.path.exists('../results'):
os.makedirs('../results')
with torch.no_grad():
z = torch.randn(64, 20).to(device)
sample = model.decode(z).cpu()
save_image(sample.view(64, 1, 28, 28), '../results/sample_' + str(epoch) + '.png')
結果
結果は以下です。

最後に
最近はローカルLLMがすごい流行っているのですが、2B程度を適当に学習を回すとかはできますが、いかんせんおおきなLLMの学習などはできる環境にありません。
そんな私でも生成系のニューラルネットワークを回したかったのです。
そんな時にお手軽にできるのはGANやVAEでした。
学生時代の研究でGANをぶん回していて辛かったので今回はVAEを回してみました。
またいつかVAEでのユースケースの紹介とかできたらたのしそうだなあ。
Xやってるのでぜひフォローお願いします。
@hudebakonosoto
Discussion