【初めて学ぶQURI Parts】VQEしてみた

今回はVQEを量子計算ライブラリを使ってやってみたい。そんな気持ちが溢れたので、国産の量子計算ライブラリであるQURI Partsを使ってVQEを実行してみようと思います。
VQEの理解も、QURI Partsの理解もまあまあ浅いので間違っている可能性があることご了承ください。

ではざっくりやっていきます！

イメージつけるために数式などを出していますが、あんまり自信ないのでご容赦ください。

QURI Partsについて

皆さん、量子計算系のライブラリといえば、何を思い浮かべますか？
qiskit？　Q#？　はたまたQulacsですか？

私はQURI Partsです。
QURI Partsは株式会社QunaSysが作っている国産の量子計算ライブラリです。
どこがいい点かはホームページに書いています
https://qunasys.com/news/posts/quri-parts/

• プラットフォーム非依存
• モジュール性と拡張性
• パフォーマンスが最高

なるほどなあ。私が特にいいと思うところは、プラットフォームやシミュレータを自由に選択できるところですね。
個人で使うにはシミュレータで全然いいですが、昨今いろんな量子コンピュータがでてきているのでいろいろプラットフォームを選べるのはいいところだと思います。

なぜVQEを使うのか？

まずですが、VQEの話からしていきたいと思います。
VQEはVariational Quantum Eigensolverの略です。これを日本語にすると変分量子固有値ソルバーです。
このことから分かるように、固有値計算をするためのアルゴリズムです。

ここは正しくないことがわかりました。

実用上は近似波動関数とエネルギー期待値を得る手法
変分的最適解を得るにはおそらく指数的なコストが必要

FTQCアルゴリズムを用いた分子の高精度量子化学計算に向けて 杉﨑研司 P.12
https://qsw.phys.s.u-tokyo.ac.jp/assets/files/20211207_sugisaki.pdf

ただ以下の記述は本当にざっくり理解するだけであれば以下の理解でもいいとはおもっています。

固有値計算といえば計算するのが大変なイメージがあります。

古典計算での固有値計算⇨ 次元が増えれば増えるほど、計算量が指数関数上に発散してしまい、計算が大変！
量子計算での固有値計算⇨ QPEを使えば効率的に計算できる！でも量子コンピュータがまだQPEをできるまで育ってないから無理！

VQEはこのちょうど中間を行こうぜ！ってアルゴリズムで、古典計算と量子計算のハイブリッドなアルゴリズムです。

VQEの計算をするイメージをつける

では実際にVQEがどんなものなのかをイメージできるように解説していきます！
実際に量子化学計算でVQEをみていきます。
一回でも量子化学計算を学んだことがある前提で書いていきますので、わからない方は辛抱して読んでください！

ざっくり変分原理(VQEの根底にある原理)

波動関数からエネルギー期待値を求めるときに以下の数式で書かれているのを目にしますね。

$$\begin{align} H | \psi \rangle = E | \psi \rangle \end{align}$$

期待値を出す時は以下のようにすればエネルギー期待値Eを取り出せます。

$$\begin{align} E = \langle \psi | H | \psi \rangle \end{align}$$

波動関数にハミルトニアンという演算子を作用させると、その固有値Eがエネルギーなどの物理量を測定できるよ！ってやつです。

次に変分原理をみていきましょう。まず数式です。

$$\begin{align} \langle \psi | H | \psi \rangle \ge E_0 \end{align}$$

$$E_0は基底エネルギー(一番安定した時のエネルギー値)$$

これは何かというと
適当に選んできた波動関数からエネルギーの期待を算出しても、一番安定した波動関数のエネルギー期待値の方が低いにきまってるやん！の原理です。

イメージ図を描きます。

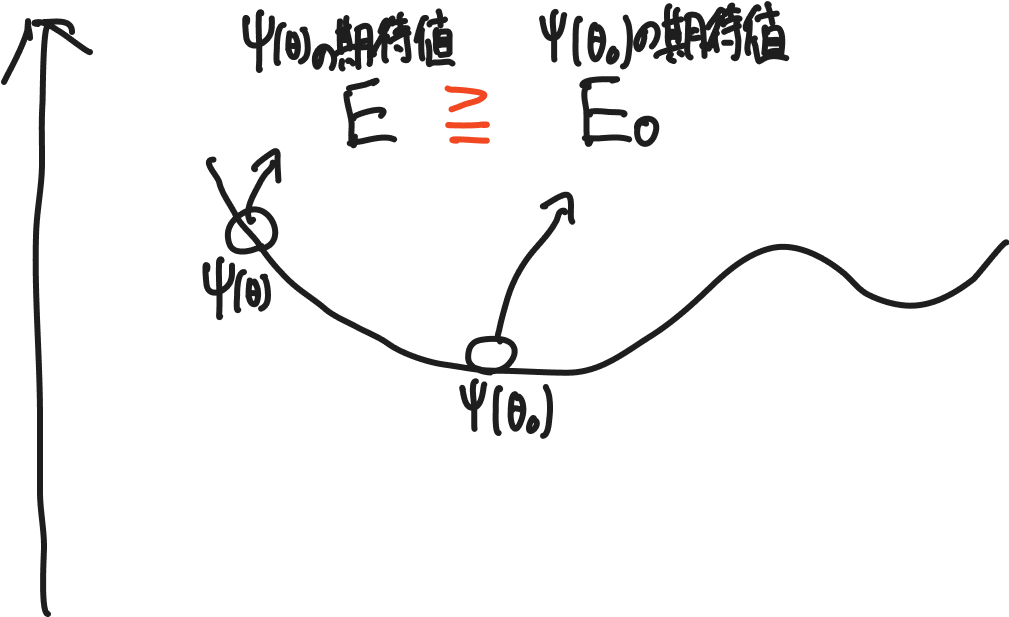
式だけ見るとよくわからないですが、割と直感に即した原理に思えます。

ざっくり変分法(VQEがやってること)

変分法は上述の性質を利用します。
まずは波動関数の持っているパラメータθを適当に決め、それを元に期待値を計算します。

$$\begin{align} \langle H(\theta) \rangle = \langle \psi (\theta) | H | \psi (\theta) \rangle \end{align}$$

これを元にパラメータθを更新します。更新の仕方はいろいろあり、勾配降下法が一番簡単に実装できる気がする(私が理解しているだけ)ので、それに沿って簡略化して説明していきます。

$$\begin{align} \frac{\partial \langle H \rangle}{\partial \theta} = \frac {\langle \psi (\theta) | H | \psi (\theta) \rangle - \langle \psi (\theta') | H | \psi (\theta') \rangle}{\theta - \theta'} \end{align}$$

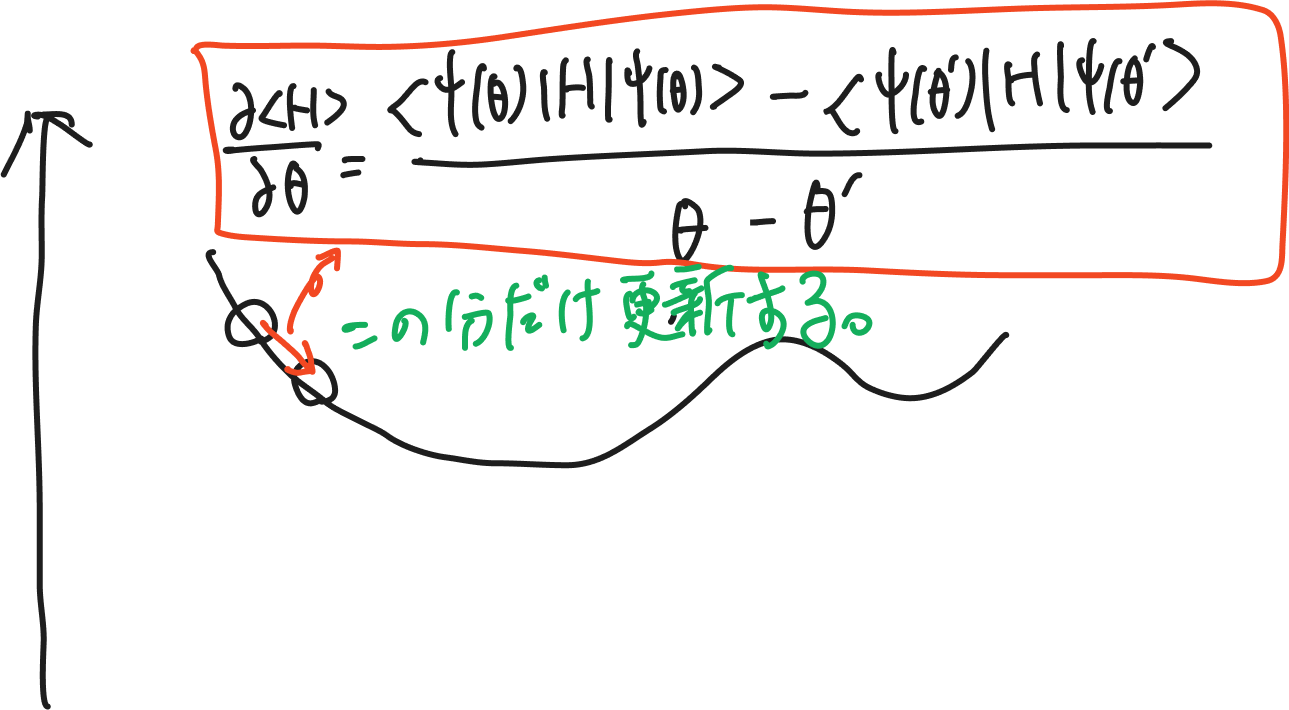
この微分して出てきた分だけパラメータθを更新することで波動関数が安定する方向に移動していきます。

$$\begin{align} \theta_{k+1} = \theta_k - \delta \frac{\partial \langle H \rangle}{\partial \theta} \end{align}$$

これを繰り返していくと、次第に波動関数が基底状態に落ち着くはず！ということです。
ただどこかでローカルミニマにハマってしまう可能性はあるので必ずしも基底状態に落ち着くとは限らないことを頭に入れておこう。

VQEは上記で述べたことを一部量子コンピュータをつかって実行しているアルゴリズムです。
では、どんなところで量子コンピュータを使っているかをみてみよう。

VQE全体像

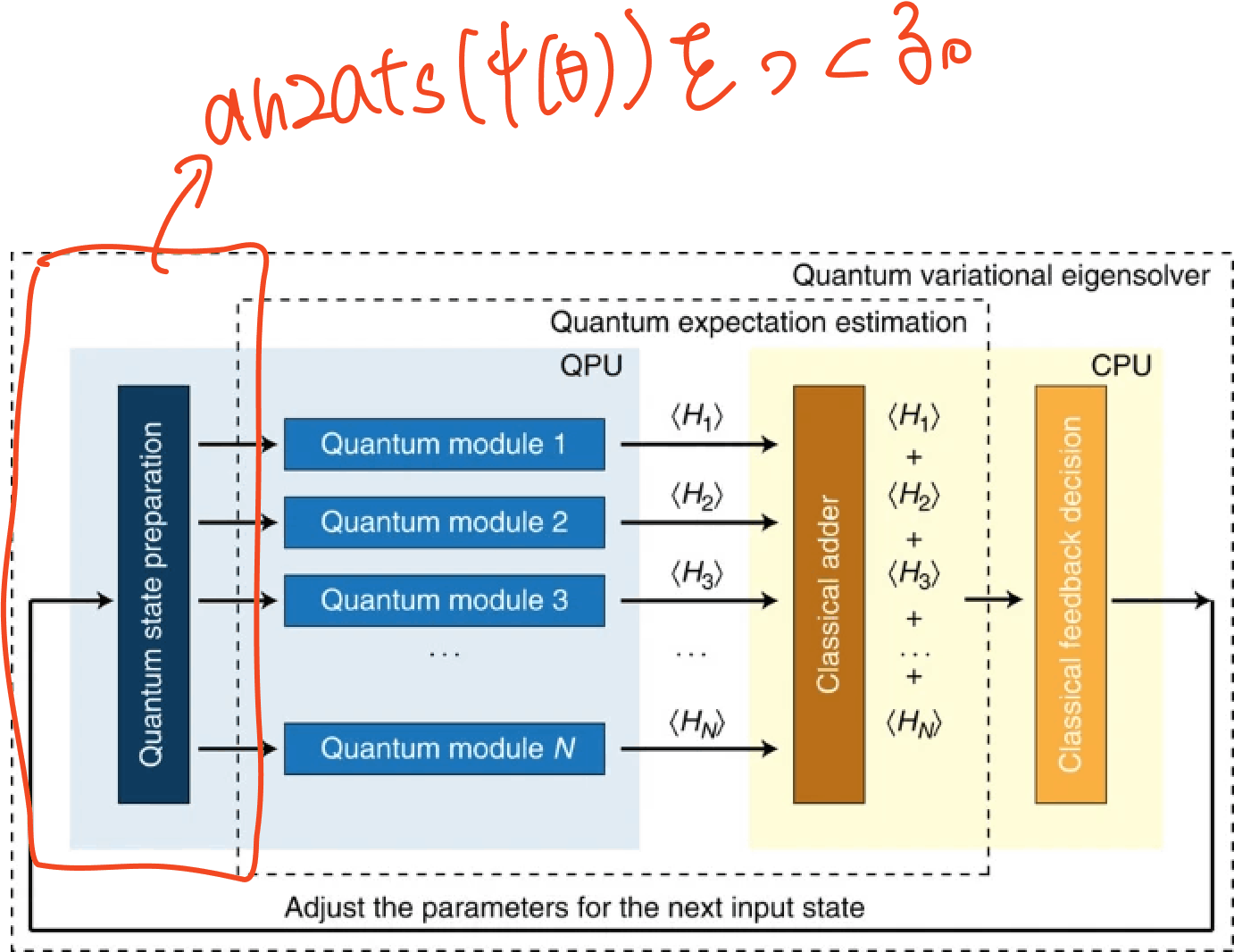
では次にVQEの全体像を見て、量子コンピュータと古典コンピュータがどんなふうに使われているかをみていきましょう。以下が全体像の図です。

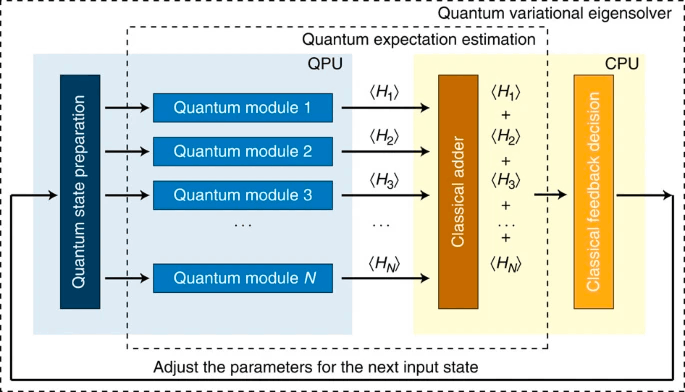
[1] A. Peruzzo et al. , “A variational eigenvalue solver on a photonic quantum processor“ Nat. Commun. 5:4213 doi: 10.1038/ncomms5213 (2014)

なるほどね。わからん。これ見ても正直わからん。なので詳しく見きましょう。

1. 期待値を計算するための演算子(ハミルトニアン)の構築
   

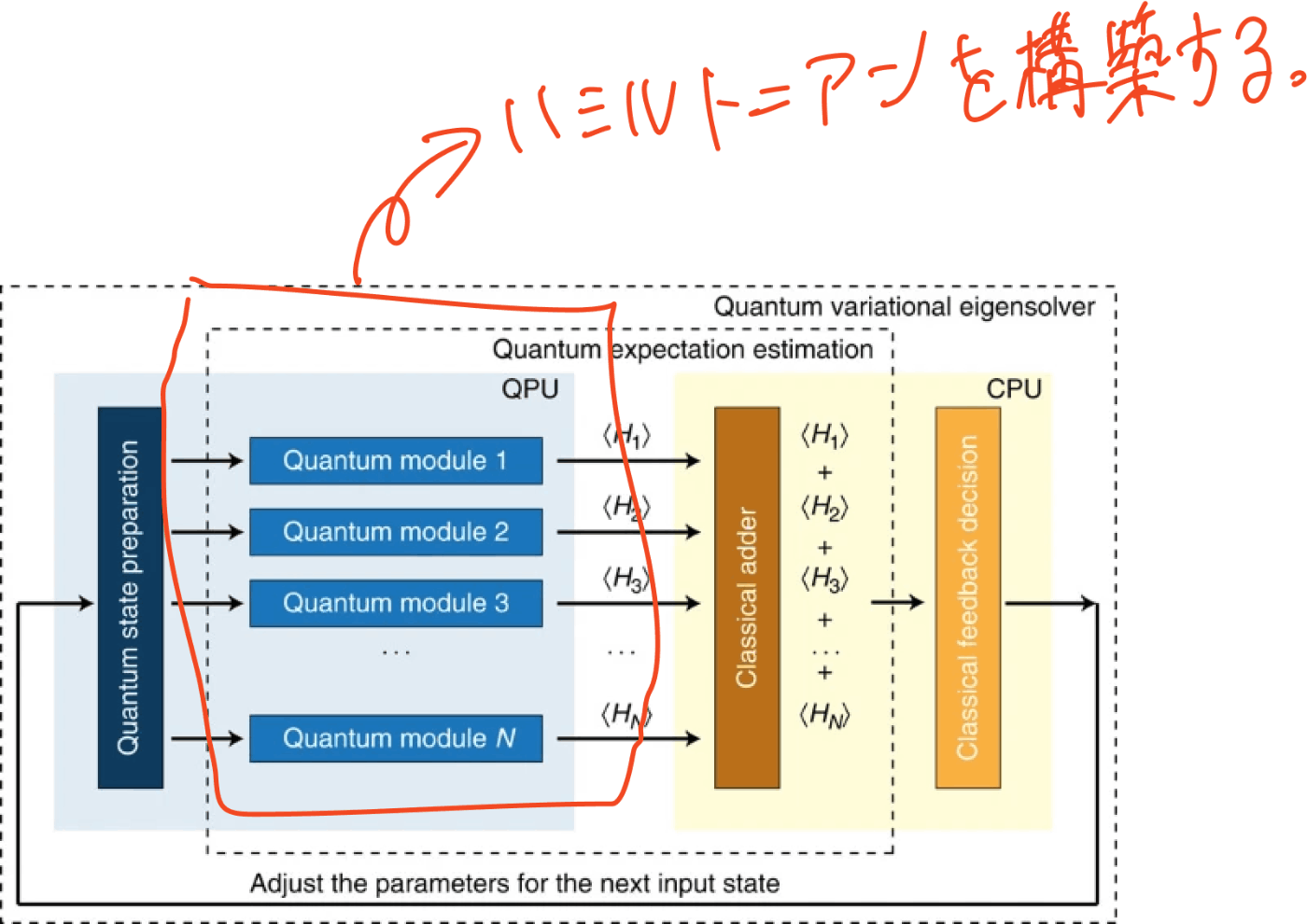
2. 量子コンピュータ内で使用する試行波動関数を作成する(Anzatsを作る)。
   

3. 量子コンピュータ側でハミルトニアンを作用＋期待値を観測して、古典コンピュータに送信する。
   

4. 勾配降下法などでパラメータを更新する。
   

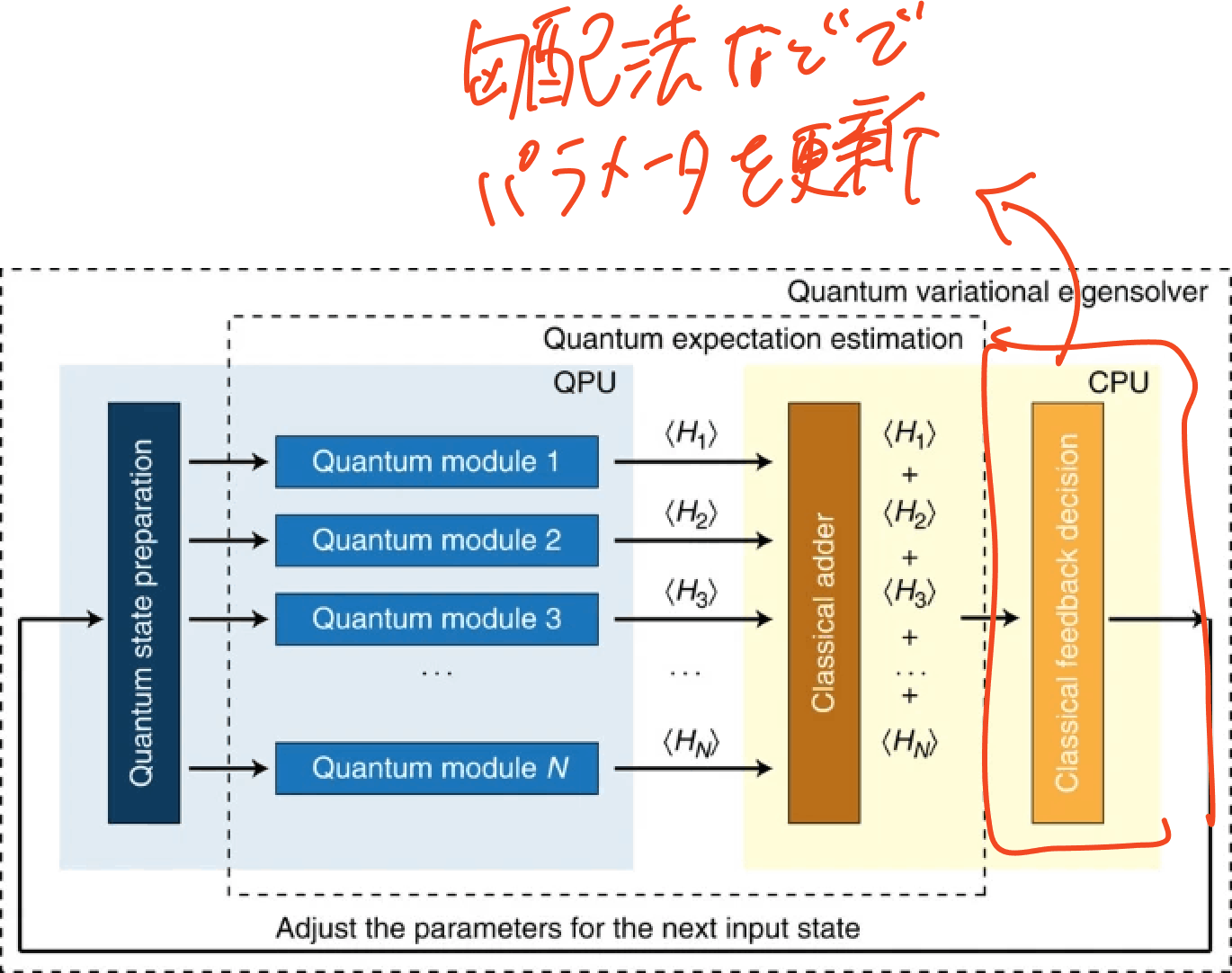
量子コンピュータ側では期待値を計算する時の処理、古典コンピュータ側ではパラメータの更新をしているということがわかりました。

VQEをつかうだけならそこまで考えることは多くないと思います。
量子化学計算と一緒にVQEを学ぶとメインどころがハミルトニアンを構築するところに見えてしまいますが、VQE自体は上述したことがメインになっています。
各ステップの詳しい内容はQURI Partsのチュートリアルとみていくとわかりやすいと思います。実際にやってみましょう。

QURI PartsでVQEを実装しよう

tutorial通りにやっていこう。
https://quri-parts.qunasys.com/tutorials/variational

まずはinstall

!pip install "quri-parts[qulacs]"

上でも書きましたが、用意するのは以下の項目！

1. 期待値を計算するための演算子(ハミルトニアン)の構築
2. 量子コンピュータ内で使用する試行波動関数を作成する(Anzatsを作る)。
3. 量子コンピュータ側でハミルトニアンを作用＋期待値を観測して、古典コンピュータに送信する。
4. 勾配降下法などでパラメータを更新する。

1. 期待値を計算するための演算子(ハミルトニアン)の構築

１のハミルトニアンは今回はQURI Partsのチュートリアルから拝借します。

from quri_parts.core.operator import Operator, pauli_label, PAULI_IDENTITY

# QURI Partsのチュートリアル参照。水素分子のハミルトニアンを量子コンピュータが受け取れる形にしたやつ！
# くわしくいうと、ハミルトニアンをパウリ演算子の形に変換したもので、これは量子コンピュータが解釈しやすい形になっている。
operator_from_hamiltonian = Operator({
    PAULI_IDENTITY: 0.03775110394645542,
    pauli_label("Z0"): 0.18601648886230593,
    pauli_label("Z1"): 0.18601648886230593,
    pauli_label("Z2"): -0.2694169314163197,
    pauli_label("Z3"): -0.2694169314163197,
    pauli_label("Z0 Z1"): 0.172976101307451,
    pauli_label("Z0 Z2"): 0.12584136558006326,
    pauli_label("Z0 Z3"): 0.16992097848261506,
    pauli_label("Z1 Z2"): 0.16992097848261506,
    pauli_label("Z1 Z3"): 0.12584136558006326,
    pauli_label("Z2 Z3"): 0.17866777775953396,
    pauli_label("X0 X1 Y2 Y3"): -0.044079612902551774,
    pauli_label("X0 Y1 Y2 X3"): 0.044079612902551774,
    pauli_label("Y0 X1 X2 Y3"): 0.044079612902551774,
    pauli_label("Y0 Y1 X2 X3"): -0.044079612902551774,
})

$$\begin{align} 0.03775110394645542*I + 0.18601648886230593*Z0 + 0.18601648886230593*Z1 + -0.2694169314163197*Z2 + -0.2694169314163197*Z3 + 0.172976101307451*Z0 Z1 + 0.12584136558006326*Z0 Z2 + 0.16992097848261506*Z0 Z3 + 0.16992097848261506*Z1 Z2 + 0.12584136558006326*Z1 Z3 + 0.17866777775953396*Z2 Z3 + -0.044079612902551774*X0 X1 Y2 Y3 + 0.044079612902551774*X0 Y1 Y2 X3 + 0.044079612902551774*Y0 X1 X2 Y3 + -0.044079612902551774*Y0 Y1 X2 X3 \end{align}$$

2. 量子コンピュータ内で使用する試行波動関数を作成する(Anzatsを作る)。

次にAnzatsを用意します！
VQEの全体像の図だとQuantum state preparationとしか書いていないのでわかりにくいのですが、詳細は以下のようになっています。

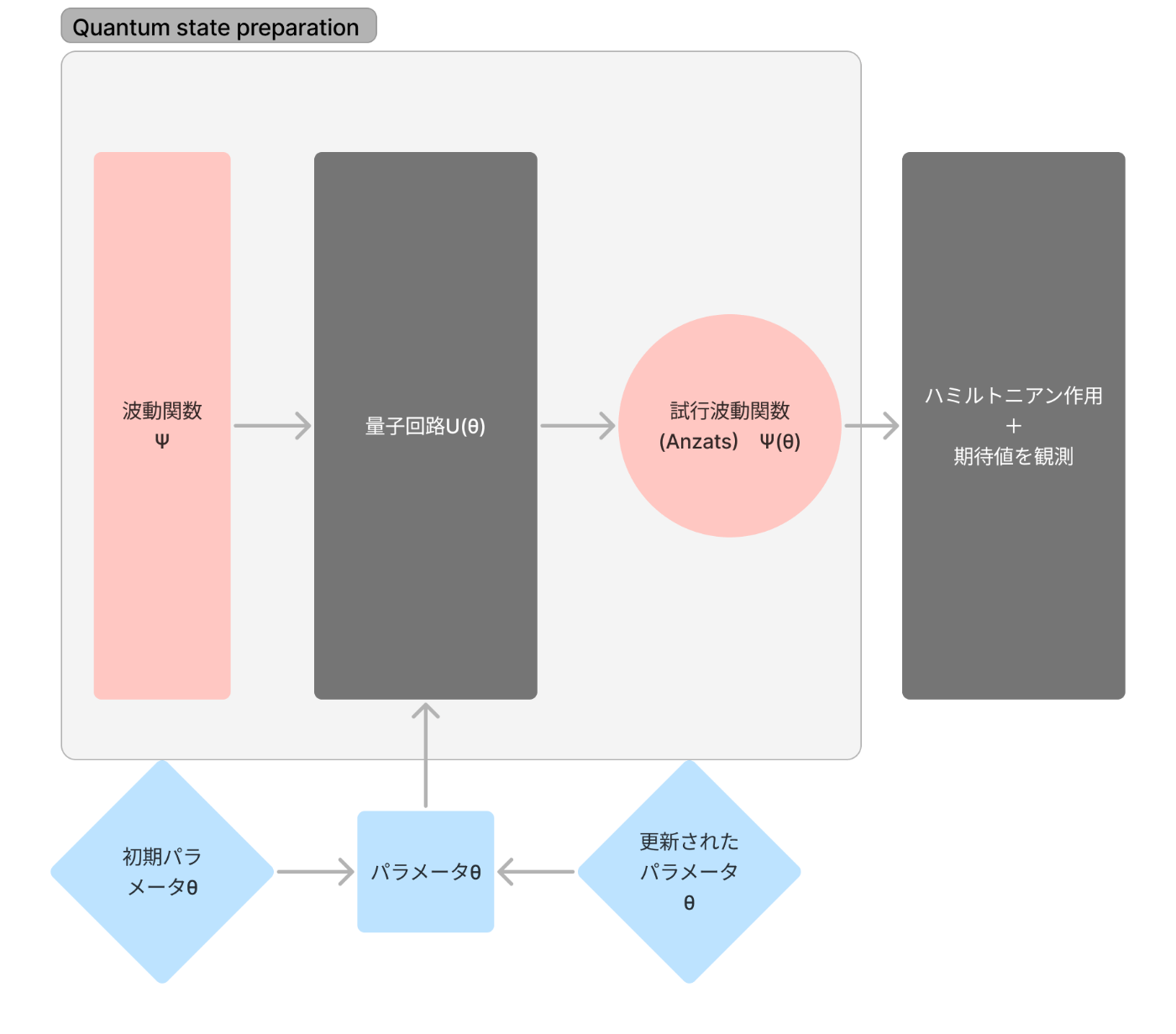
Anzatsは試行波動関数です。試行波動関数を生成する量子回路自体がAnzatsと呼ばれることがありますが、作成された波動関数自体がAnzatsと呼ばれるみたいです。しかし慣習的に量子回路自体がAnzatsとよばれているみたいです。
量子化学に関してはAnzatsは電子相関を取り込むことができるとかどうとか...
Anzatsにはいろいろと種類がありますが、今回はHardwareEfficientAnzatsを使用します。

from quri_parts.algo.ansatz import HardwareEfficient
from quri_parts.circuit.utils.circuit_drawer import draw_circuit
from quri_parts.core.state import ParametricCircuitQuantumState

# これでAnzatsが用意できる。
hwe_ansatz = HardwareEfficient(qubit_count=4, reps=3)

# Anzatsはパラメトリックな量子回路なので、ParametricCircuitQuantumStateを使用してパラメータを与えれるようにします
# https://quri-parts.qunasys.com/tutorials/parametric#Parametric-state-and-operator-expectation-estimation
hwe_parametric_state = ParametricCircuitQuantumState(n_qubits=4, circuit=hwe_ansatz)

3. 量子コンピュータ側でハミルトニアンを作用＋期待値を観測して、古典コンピュータに送信する。

1で用意したハミルトニアンを試行波動関数に作用させます。そして出てきたものを観測します！おわり！！
コードは次の項目に含めます！

4. 勾配降下法などでパラメータを更新する。

最後に変分法を用いた最適化手法が使ってパラメータを更新していきます！
変分法の解説で以下のように書いたやつです！

$$\begin{align} \frac{\partial \langle H \rangle}{\partial \theta} = \frac {\langle \psi (\theta) | H | \psi (\theta) \rangle - \langle \psi (\theta') | H | \psi (\theta') \rangle}{\theta - \theta'} \end{align}$$

ただし上記で書いたやつは一次元まで落ちているかつ、数値微分の計算になっているので数式っぽいのも書いておきます！実際計算で使っているのは数値微分の計算をもっと次元を増やして行列にしたやつ。(たぶん、知らんけど)

$$\begin{align} \nabla_\theta H(\theta) = \left( \frac{\partial \langle H \rangle_\theta}{\partial \theta_0}, \ldots, \frac{\partial \langle H \rangle_\theta}{\partial \theta_{m-1}} \right) \end{align}$$

では最適化を考えますが、ここで意識しておかないといけないのがコスト関数です。コスト関数は何を最小化するかの指標となるものです。今回はエネルギー自体がコスト関数の指標となります。
エネルギーを最小化するように勾配を降りていきます。
QURI Partsではこのコスト関数と勾配関数(どうやって勾配を計算するか、今回は微分して勾配を算出する)を決めないといけません。なので、以下のように定義しましょう。(チュートリアル準拠)

コスト関数

from quri_parts.qulacs.estimator import create_qulacs_vector_parametric_estimator
# Estimatorについては以下を参照してください。簡単にいうと演算子の期待値を推定するためのやつです
# https://quri-parts.qunasys.com/tutorials/estimator_basics#Estimator
estimator = create_qulacs_vector_parametric_estimator()

# 今回最適化するためのコスト関数。水素のハミルトニアンから得られる期待値がコスト関数。(基底エネルギーがコスト関数になっているみたいと思ってる。)
def cost_fn(param_values):
   # ハミルトニアンは最初に定義したやつを使う
   # 演算子と状態を渡すと演算子の期待値を推定できる
    estimate = estimator(operator_from_hamiltonian, hwe_parametric_state, param_values)
    return estimate.value.real

勾配関数

import numpy as np
from quri_parts.core.estimator.gradient import create_numerical_gradient_estimator
from quri_parts.qulacs.estimator import (
    create_qulacs_vector_concurrent_parametric_estimator,
)

qulacs_concurrent_parametric_estimator = (
    create_qulacs_vector_concurrent_parametric_estimator()
)

# 数値勾配を定義
# deltaはどのぐらいの刻みで動かすかを定義している。小さすぎても大きすぎてもダメ。いいところにするべし
gradient_estimator = create_numerical_gradient_estimator(
    qulacs_concurrent_parametric_estimator,
    delta=1e-4,
)

# 数値勾配を実行するための勾配関数
def grad_fn(param_values):
    estimate = gradient_estimator(
        operator_from_hamiltonian, hwe_parametric_state, param_values
    )
    return np.asarray([g.real for g in estimate.values])

ここまででVQEを実行するための準備が完了しました！最後に以下を実行して、VQEを実行してみましょう
下記のコードでは以下のようにパラメトリックな量子回路を更新していくことになります。

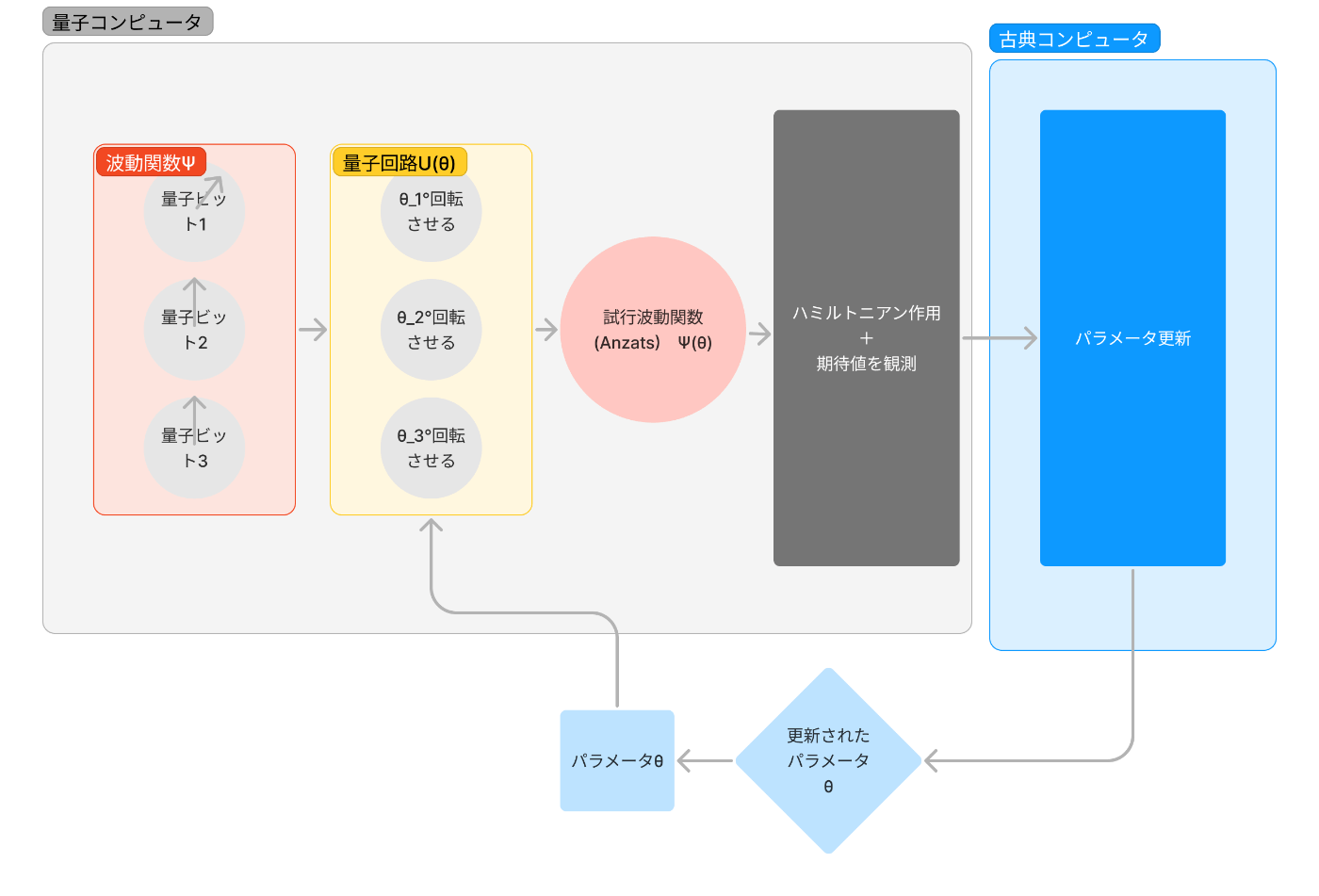
import random
from quri_parts.algo.optimizer import OptimizerStatus
from quri_parts.algo.optimizer import Adam

# vqe実行
# チュートリアルにoperatorが引数に入っているけどいらない？
def vqe(operator, init_params, cost_fn, grad_fn, optimizer):

    opt_state = optimizer.get_init_state(init_params)
    energy_hist = []

    while True:
        opt_state = optimizer.step(opt_state, cost_fn, grad_fn)
        energy_hist.append(opt_state.cost)

        if opt_state.status == OptimizerStatus.FAILED:
            print("Optimizer failed")
            break

        if opt_state.status == OptimizerStatus.CONVERGED:
            print("Optimizer converged")
            break

    return opt_state, energy_hist




# 最初の試行波動関数を作るためのランダムな初期パラメータ
init_params = [random.random() for _ in range(hwe_ansatz.parameter_count)]

# オプティマイザーを定義
optimizer = Adam()

# VQEを実行
result, energy_hist = vqe(operator_from_hamiltonian, init_params, cost_fn, grad_fn, optimizer)

print("Optimized value:", result.cost)
print("Optimized parameter:", result.params)
print("Iterations:", result.niter)
print("Cost function calls:", result.funcalls)
print("Gradient function calls:", result.gradcalls)

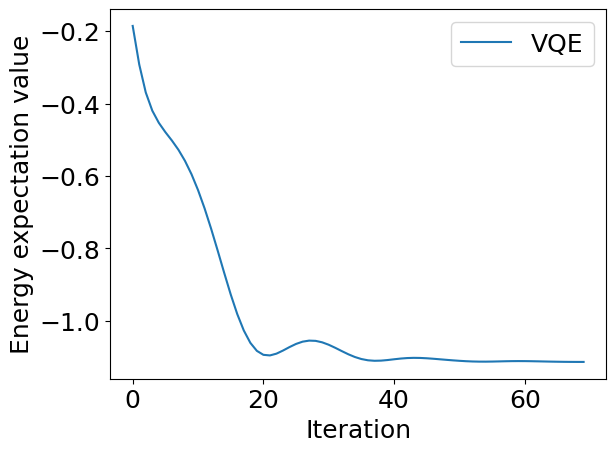
ただしく収束しているかを確認しておわりです。

import matplotlib.pyplot as plt

plt.plot(energy_hist, label="VQE")

plt.xlabel("Iteration")
plt.ylabel("Energy expectation value")
plt.legend()
plt.show()

収束してる！それっぽい！ヨシ！！！

QURI PartsでのVQE実装まとめ

import matplotlib.pyplot as plt

import random
import numpy as np
from quri_parts.algo.optimizer import OptimizerStatus
from quri_parts.algo.optimizer import Adam


from quri_parts.algo.ansatz import HardwareEfficient
from quri_parts.circuit.utils.circuit_drawer import draw_circuit
from quri_parts.core.state import ParametricCircuitQuantumState
from quri_parts.qulacs.estimator import create_qulacs_vector_parametric_estimator
from quri_parts.core.estimator.gradient import create_numerical_gradient_estimator
from quri_parts.qulacs.estimator import (
    create_qulacs_vector_concurrent_parametric_estimator,
)
from quri_parts.core.operator import Operator, pauli_label, PAULI_IDENTITY

# QURI Partsのチュートリアル参照。水素分子のハミルトニアンを量子コンピュータが受け取れる形にしたやつ！
# くわしくいうと、ハミルトニアンをパウリ演算子の形に変換したものでこれだと量子コンピュータで受け取れる形
operator_from_hamiltonian = Operator({
    PAULI_IDENTITY: 0.03775110394645542,
    pauli_label("Z0"): 0.18601648886230593,
    pauli_label("Z1"): 0.18601648886230593,
    pauli_label("Z2"): -0.2694169314163197,
    pauli_label("Z3"): -0.2694169314163197,
    pauli_label("Z0 Z1"): 0.172976101307451,
    pauli_label("Z0 Z2"): 0.12584136558006326,
    pauli_label("Z0 Z3"): 0.16992097848261506,
    pauli_label("Z1 Z2"): 0.16992097848261506,
    pauli_label("Z1 Z3"): 0.12584136558006326,
    pauli_label("Z2 Z3"): 0.17866777775953396,
    pauli_label("X0 X1 Y2 Y3"): -0.044079612902551774,
    pauli_label("X0 Y1 Y2 X3"): 0.044079612902551774,
    pauli_label("Y0 X1 X2 Y3"): 0.044079612902551774,
    pauli_label("Y0 Y1 X2 X3"): -0.044079612902551774,
})

print(operator_from_hamiltonian)



# これでAnzatsが用意できる。
hwe_ansatz = HardwareEfficient(qubit_count=4, reps=3)

# Anzatsはパラメトリックな量子回路なので、ParametricCircuitQuantumStateを使用してパラメータを与えれるようにします
# https://quri-parts.qunasys.com/tutorials/parametric#Parametric-state-and-operator-expectation-estimation
hwe_parametric_state = ParametricCircuitQuantumState(n_qubits=4, circuit=hwe_ansatz)


# Estimatorについては以下を参照してください。簡単にいうと演算子の期待値を推定するためのやつです
# https://quri-parts.qunasys.com/tutorials/estimator_basics#Estimator
estimator = create_qulacs_vector_parametric_estimator()

# 今回最適化するためのコスト関数。水素のハミルトニアンから得られる期待値がコスト関数。(基底エネルギーがコスト関数になっているみたいと思ってる。)
def cost_fn(param_values):
   # ハミルトニアンは最初に定義したやつを使う
   # 演算子と状態を渡すと演算子の期待値を推定できる
    estimate = estimator(operator_from_hamiltonian, hwe_parametric_state, param_values)
    return estimate.value.real


qulacs_concurrent_parametric_estimator = (
    create_qulacs_vector_concurrent_parametric_estimator()
)

# 数値勾配を定義
# deltaはどのぐらいの刻みで動かすかを定義している。小さすぎても大きすぎてもダメ。いいところにするべし
gradient_estimator = create_numerical_gradient_estimator(
    qulacs_concurrent_parametric_estimator,
    delta=1e-4,
)

# 数値勾配を実行するための勾配関数
def grad_fn(param_values):
    estimate = gradient_estimator(
        operator_from_hamiltonian, hwe_parametric_state, param_values
    )
    return np.asarray([g.real for g in estimate.values])


# vqe実行
# チュートリアルにoperatorが引数に入っているけどいらない？
def vqe(operator, init_params, cost_fn, grad_fn, optimizer):

    opt_state = optimizer.get_init_state(init_params)
    energy_hist = []

    while True:
        opt_state = optimizer.step(opt_state, cost_fn, grad_fn)
        energy_hist.append(opt_state.cost)

        if opt_state.status == OptimizerStatus.FAILED:
            print("Optimizer failed")
            break

        if opt_state.status == OptimizerStatus.CONVERGED:
            print("Optimizer converged")
            break

    return opt_state, energy_hist




# 最初の試行波動関数を作るためのランダムな初期パラメータ
init_params = [random.random() for _ in range(hwe_ansatz.parameter_count)]

# オプティマイザーを定義
optimizer = Adam()

# VQEを実行
result, energy_hist = vqe(operator_from_hamiltonian, init_params, cost_fn, grad_fn, optimizer)

print("Optimized value:", result.cost)
print("Optimized parameter:", result.params)
print("Iterations:", result.niter)
print("Cost function calls:", result.funcalls)
print("Gradient function calls:", result.gradcalls)


# 収束しているか確認
plt.plot(energy_hist, label="VQE")

plt.xlabel("Iteration")
plt.ylabel("Energy expectation value")
plt.legend()
plt.show()

終わりに

解説自体は長かったですが、VQE自体は結構シンプルでしたね。
QURI Partsをさわってみた所感としては、コードは長くなりがちになりそうだなと感じました。
qiskitだと結構あっさりかけるのですが、QURI Partsはいろいろ定義しないといけないです。
その代わりいいことが結構ありますね。

1. QURI Partsを触りながらの学習ができる
   かなり細かくモジュール化されているので、一個一個コードの意味を追いながら定義できる

2. モジュールの入れ替えが色々できそう
   VQEなどの各中間アウトプット自体はどのライブラリもたいして変わらないので、他のライブラリのいいところなどを切り取って使うとかできそうですね。

もっといろいろと触ってみたいですね。次はQURI Partsをつかって量子化学計算をVQEで計算しようと思います！

参考文献

• QURI Partsチュートリアル
  https://quri-parts.qunasys.com/tutorials/variational

• Qiskit Nature - 量子化学計算
  https://www.youtube.com/watch?v=v2fnmtZE45o

• 5-1. Variational Quantum Eigensolver（VQE）アルゴリズム　　| Quantum Native Dojo
  https://dojo.qulacs.org/ja/latest/notebooks/5.1_variational_quantum_eigensolver.html

• 量子コンピュータ勉強会レポート（その３） ～量子コンピュータ上での量子化学計算～ | HPCシステムズ Tech Blog https://www.hpc.co.jp/tech-blog/2021/01/14/quantum-computer_report_3/