⚙️
イメージで理解するPID(pythonアニメーション)

2024/11/04に公開
Python 3
 PIDって？フィードバック制御の一つで、比例要素、微分要素、積分要素を使用し、目標値に制御するものです。また、PIDのゲイン調整は経験則的に調整を行うことが多いので自由度の高いフィードバック制御として重宝されています。

 イメージ的に理解しよう今回は、pythonのmatplotlibを使って視覚的に理解することを目標とします。

モデルケースとしてPIDを使って車輪付きの台車を目標の位置（100m先など）に持っていくことを考えます。また、台車には摩擦が働くものとして考えます。

PIDではどの程度台車を押すかどうかを逐次的に計算することで目標位置に近づけていきます。

このとき押す力の強さをU(t)、目標地点との距離をe(t)、ゲインをP_{gain}、I_{gain}、D_{gain}とすると、

U(t)=P_{gain}\ e(t) + I_{gain}\ \int_{T}\ e(t)\ \delta \ t + D_{gain}\ \dfrac{\delta\ e(t)}{\delta\ t}
と表すことができます。

このとき、P、I、Dのそれぞれの要素ごとに考えていきます。

 P要素P要素のみを考えると

U(t)=P_{gain}\ e(t)
となります。とりあえず近づくことのみを考える要素です。目標値が遠ければ遠いほど強く台車を押そうというものです。このときP_{gain}の大きさを適当な大きさにすることでどのくらいの遠さでどのくらい強く台車を押すかを考えます。

pythonでシミュレーションしてみるとこんな感じ...

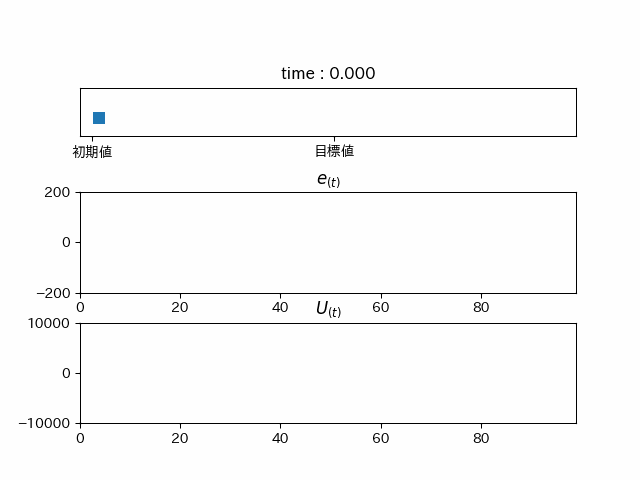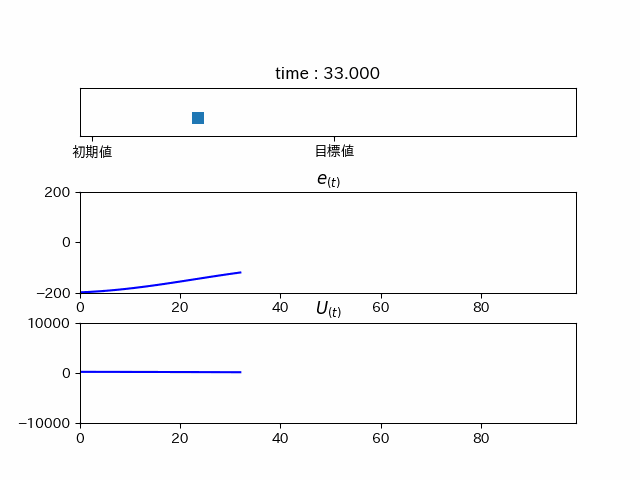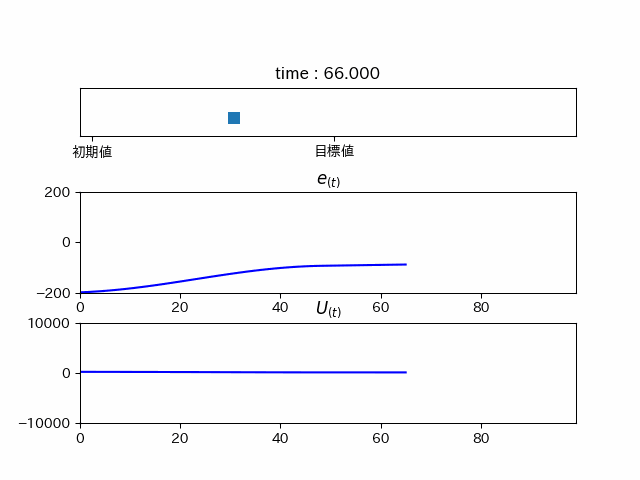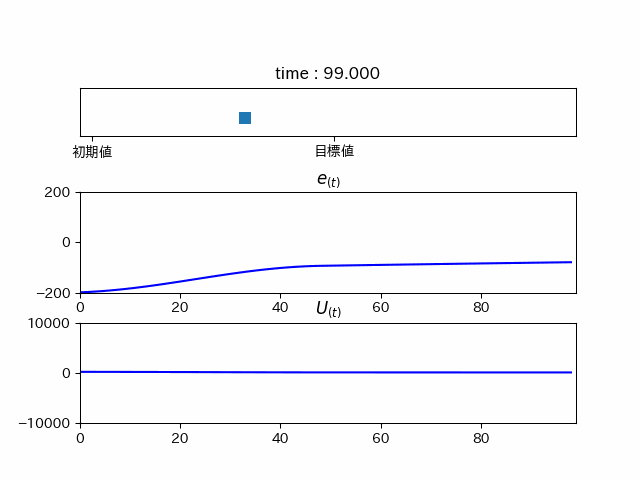
力が足りずこれ以上進みません... しかし、このままではこれはPゲインが小さいだけでは? となってしまうので、Pゲインを高くしてみると...



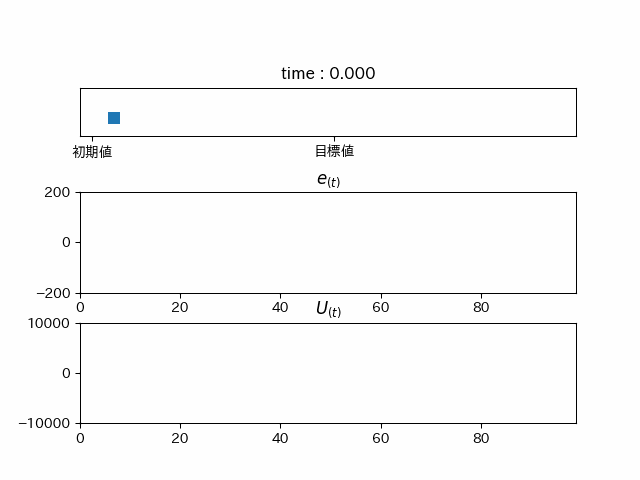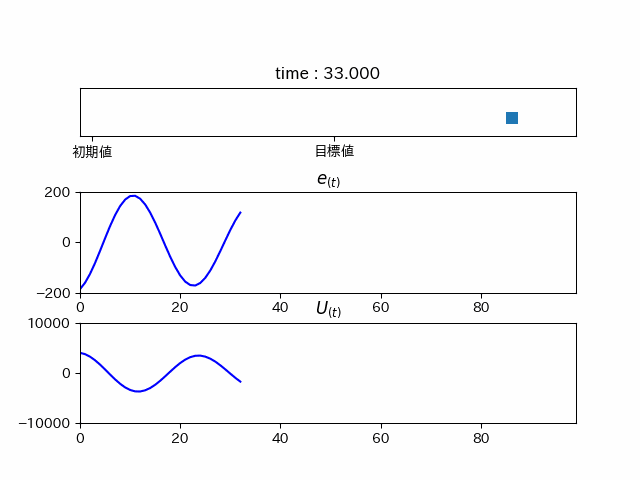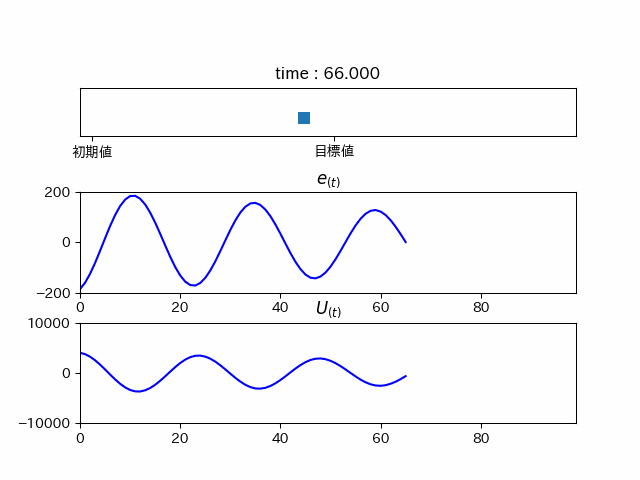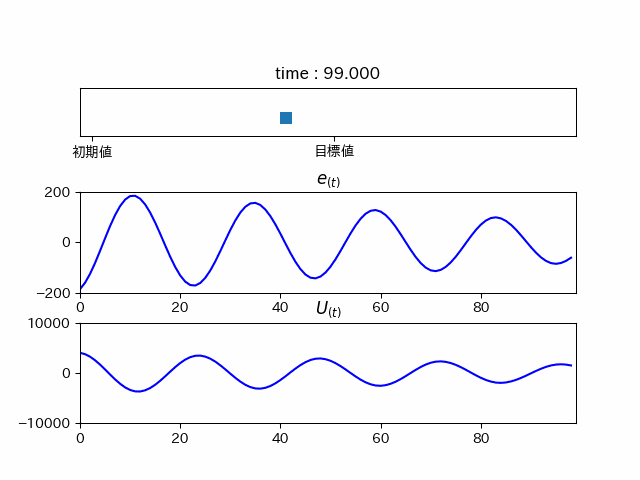
右に行ったり左に行ったりしています（振動している）。

また、このPゲインのみの制御では摩擦の大きさが少し変わるだけで大きく挙動が変わってしまいます。 そのため、I、D要素を考えていきます。

 I要素I要素はP要素の時に発生した問題これ以上進まない を解決していきます。

I要素では少しずつU(t)を強くすることで台車を進ませます。そのとき、e(t)を蓄積していくことで少しづつ強くなっていく要素を作り出し、それをU(t)に加えていきます。

U(t)=P_{gain}\ e(t) + I_{gain}\ \int_{T}\ e(t)\ \delta \ t
I要素のみを見ると

U(t)=I_{gain}\ \int_{T}\ e(t)\ \delta \ t
となります。本当に徐々にU(t)が強くなっているのか見てみましょう。



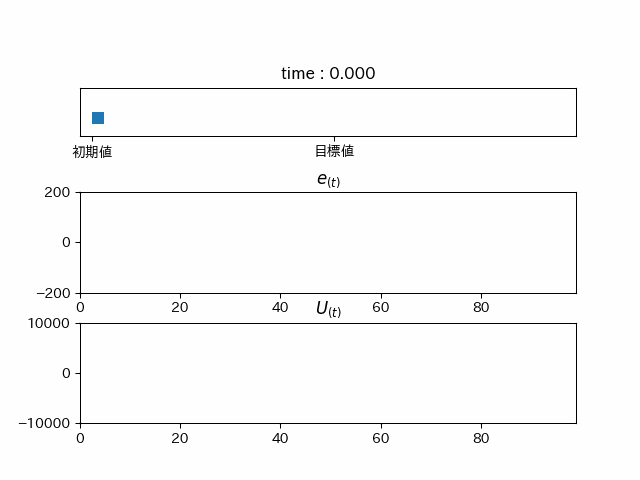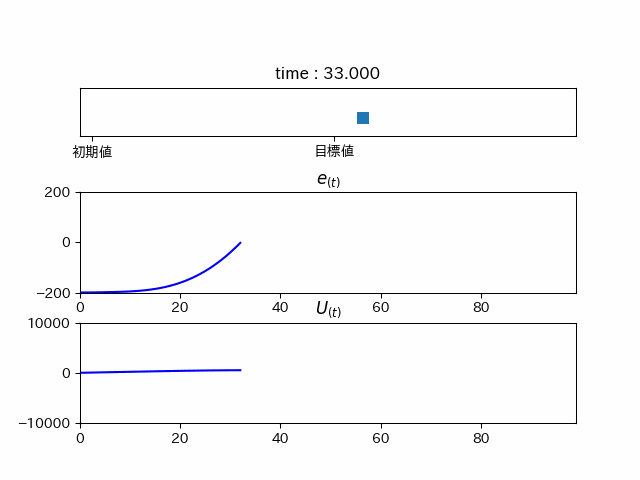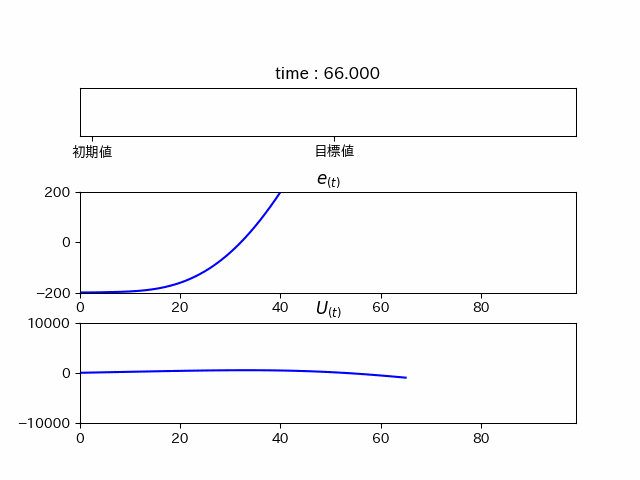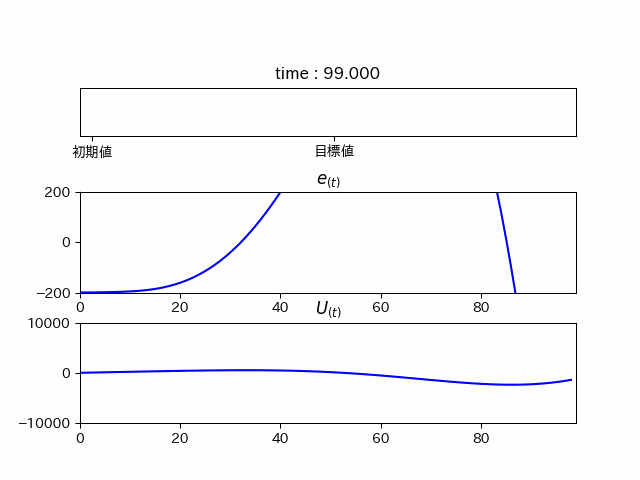
実際に強くなっていることが分かります。(吹き飛んでしまいますが...)
先ほどのP要素と合わせると...

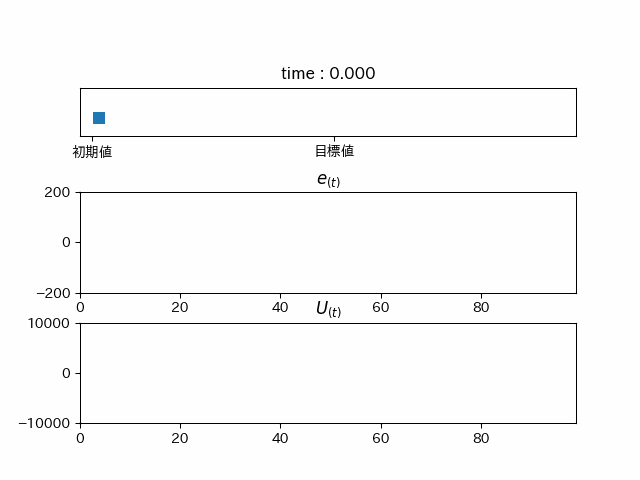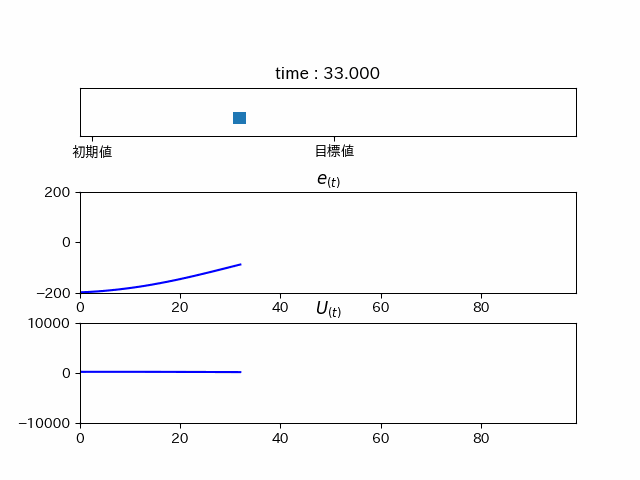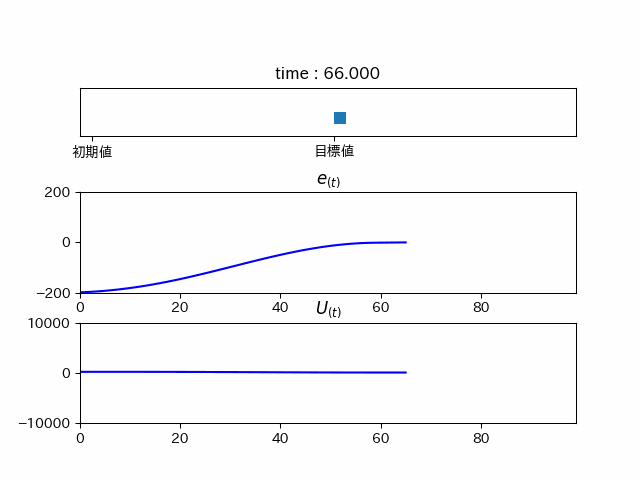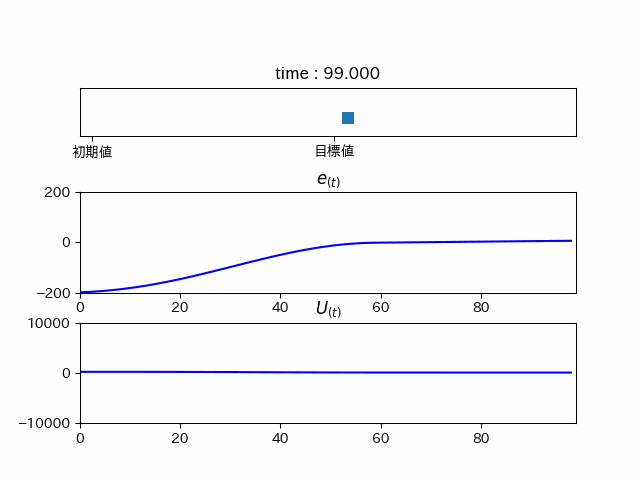
少し行き過ぎてしまっていますが、Pのみよりもうまく制御できています。

この制御方法をPI制御といいます。この制御では行き過ぎてしまう(オーバーシュート)ため制御としては微妙です。

 D要素PI制御の行き過ぎてしまうのは台車が加速しすぎてしまい、目標地点に到達しても止まれないということが発生します(オーバーシュート)。 そのため、加速しすぎを防ぐために目標値への近づき方を使って摩擦のようなブレーキをかけます。

U(t)=P_{gain}\ e(t) + I_{gain}\ \int_{T}\ e(t)\ \delta \ t + D_{gain}\ \dfrac{\delta\ e(t)}{\delta\ t}
今回の D要素は単体で見ることはできません（力を加える要素ではないので）。 そのため、P要素の時の振動していたものにD要素を加えてみます。

U(t)=P_{gain}\ e(t) + D_{gain}\ \dfrac{\delta\ e(t)}{\delta\ t}
理論どうりなら少しづつ振動が小さくなっていくはずです。

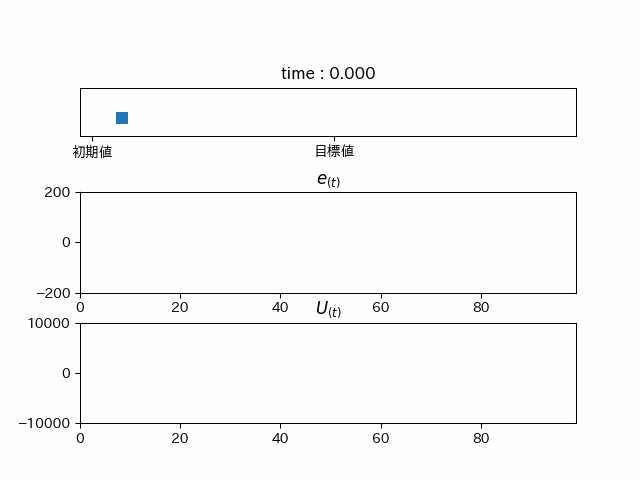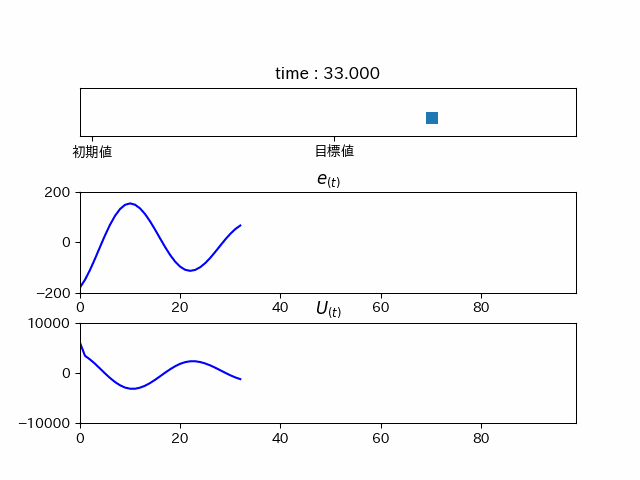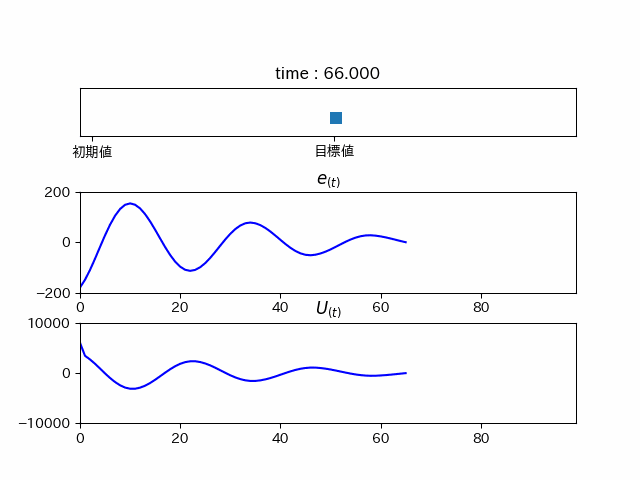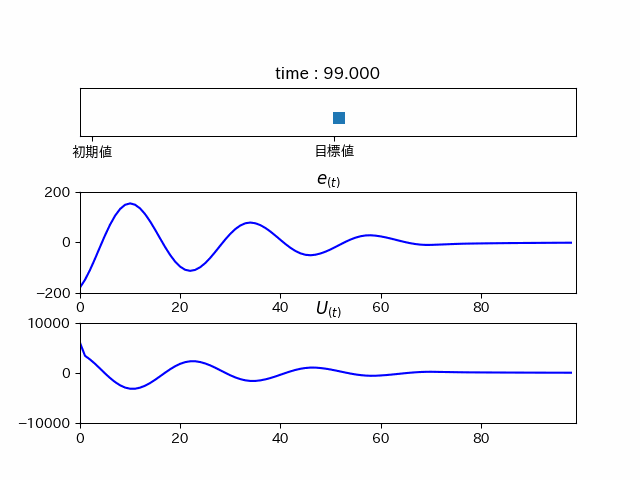
だんだん小さくなっていくことが分かります。確かに加速を抑制しています。 これをPD制御といいます。
これまでの三つの要素を合わせてPID制御を行うと...



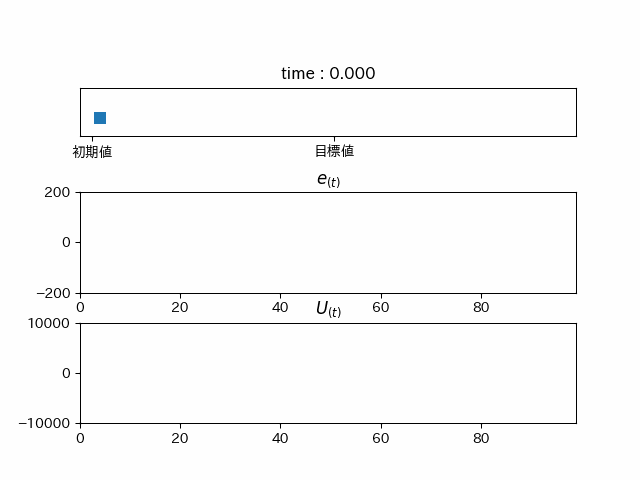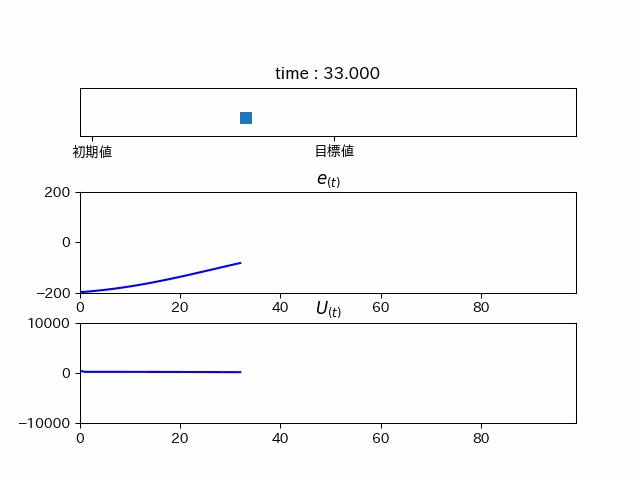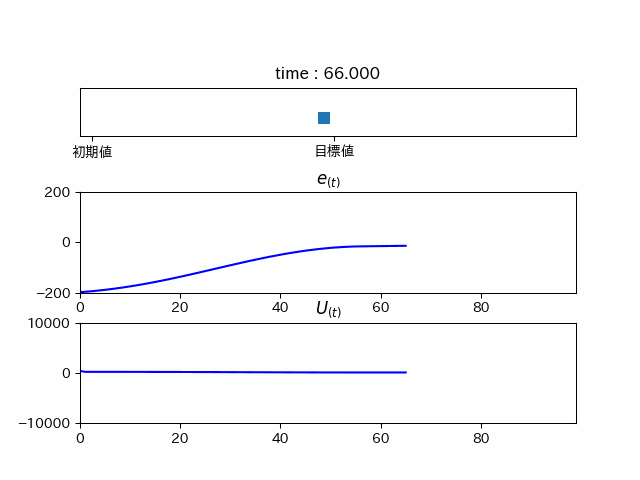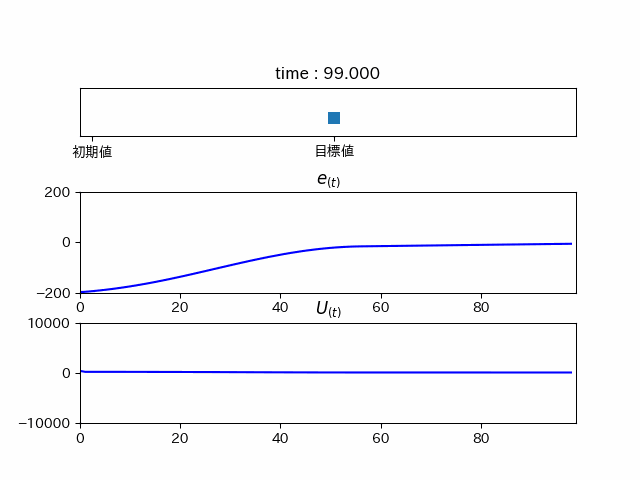
綺麗に目標地点に行っていることが分かります。しかし、これでは時間がかかりすぎてるので、ゲインを調整すると...


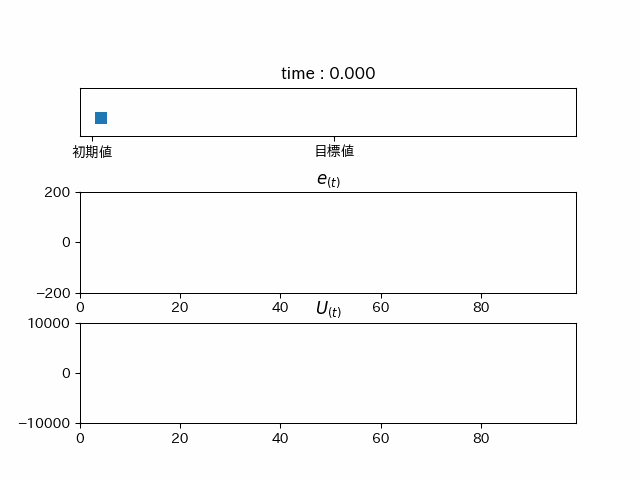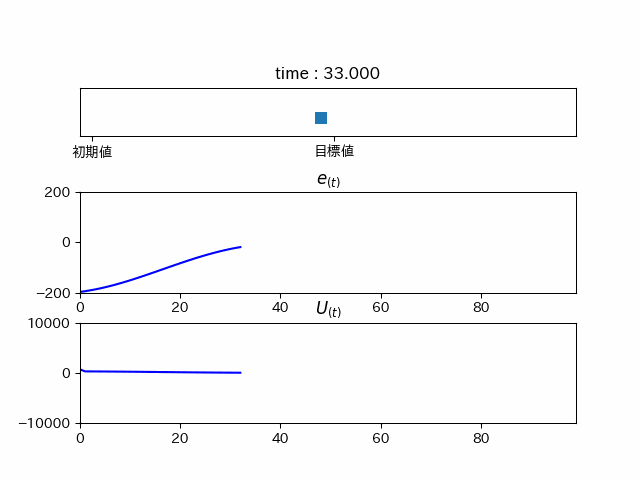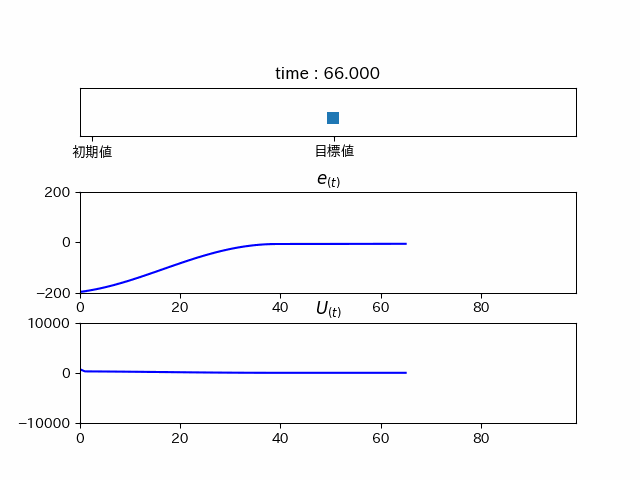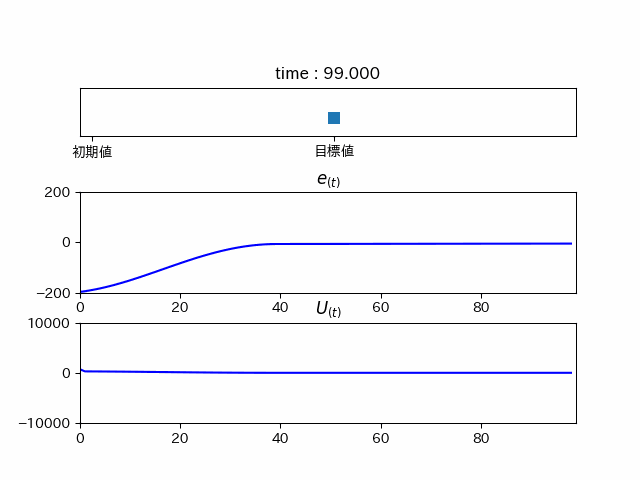
 最後にこのようにPIDを使うことで目標に瞬時に近づけることができます。

また、PIDは数値を更新する頻度を増やすとPIDの精度を高めることができます。

今回のPIDのアニメーションのpythonのコードはこのようになっています。
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
import matplotlib.patches as pat
from matplotlib.animation import FuncAnimation

class controlObject:
    def __init__(self,time):
        self.g = 9.8
        self.m = 300
        self.x = 0
        self.v = 0
        self.k = 0.05

        self.Time = time.copy()

        self.fig,[self.ax,self.ax1,self.ax2] = plt.subplots(3)

        self.logData = {"x":[],"v":[],"F":[]}
    def move(self,dt):
        self.x += self.v*dt
        self.Friction(dt)

        self.logData["x"].append(self.x)
        self.logData["v"].append(self.v)
    def Accel(self,F,dt):
        self.v += F/self.m*dt
        self.logData["F"].append(F)
    def Friction(self,dt):
        frictionForce = self.k*self.m*self.g
        v = self.v
        if(abs(self.v) >  np.sign(self.v)*frictionForce/self.m*dt):
            self.v -= np.sign(self.v)*frictionForce/self.m*dt
        else:
            self.v = 0.0
    def animFunc(self,i):
        self.ax.cla()
        self.ax.set(xlim = (-10,400),ylim = (-10,30),aspect=1,title = "time : %5.3lf" % self.Time[i])
        self.ax.yaxis.set_visible(False)
        self.ax.set_xticks([0,200])
        self.ax.set_xticklabels(["初期値","目標値"])
        objRect = pat.Rectangle((self.logData["x"][i],0),10,10)
        Rect = self.ax.add_patch(objRect)
        self.ax1.cla()
        self.ax1.set_title(r"$e_{(t)}$")
        self.ax1.set(xlim = (0,self.Time[-1]),ylim = (-200,200),aspect = 0.05)
        self.ax1.plot(self.Time[:i],np.array(self.logData["x"][:i])-200,c='b')
        self.ax2.cla()
        self.ax2.set_title(r"$U_{(t)}$")
        self.ax2.set(xlim = (0,self.Time[-1]),ylim = (-10000,10000),aspect = 0.001)
        self.ax2.plot(self.Time[:i],self.logData["F"][:i],c='b')



def main():
    deltaT = 1

    Time = np.arange(0,100,deltaT)
    obj = controlObject(Time)
    
    Target = 200

    Integral = 0
    Pro = 0

    Gains = {"P":1.5,"I":0.00001,"D":2.0}

    for i in Time:
        Diff = ((Target - obj.x) - Pro)/deltaT
        Integral += (Pro + (Target - obj.x))*deltaT/2.0
        Pro = Target - obj.x
        output = Gains["P"]*(Target - obj.x) + Gains["I"]*Integral + Gains["D"]*Diff
        obj.Accel(output,deltaT)
        obj.move(deltaT)
        

    anim = FuncAnimation(obj.fig,obj.animFunc, np.arange(Time.shape[0]),interval= 1,repeat = False)
    plt.show()


if __name__ == "__main__":
    main()
PIDって？

イメージ的に理解しよう

P要素

I要素

D要素

最後に

Discussion
