三角波生成回路の作成

はじめに

電子工作初学者の備忘録です。本記事ではLTspiceによるシミュレーションと実際の回路制作を通じて三角波生成回路への理解を深めていきます。

三角波生成回路は積分回路とヒステリシスコンパレータの組み合わせで実現できます。記事の前半で積分回路、ヒステリシスコンパレータの説明を、後半で三角波生成回路の説明と実装を行います。

積分回路

単純な積分回路

図１：積分回路
図１は一番シンプルな積分回路の例です。構造としては反転増幅回路の帰還抵抗をコンデンサに置き換えた回路となっています。入力電圧$v_{in}$と出力電圧$v_{out}$の関係は式(1)のようになります。

$$v_{out} = - \frac{1}{R_{1}C_{1}} \int{v_{in}} dt \tag{1}$$

シャント抵抗付き積分回路

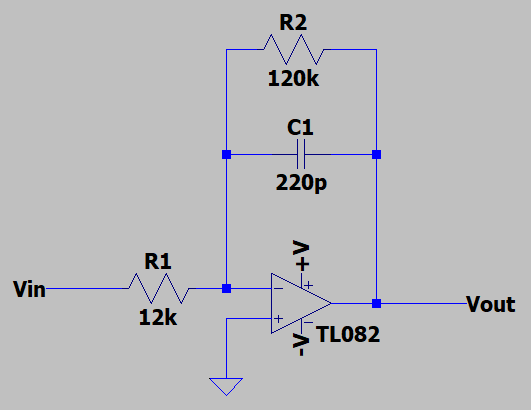
図２：シャント抵抗付き積分回路
図２はコンデンサ$C_1$にシャント抵抗$R_2$を並列接続した一般的によく用いられる積分回路です。実際の回路では、様々な原因（オペアンプの入力オフセット電圧など）によって入力信号（交流信号）に意図しない直流信号が混ざります。直流信号が積分動作すると、出力電圧がオペアンプの出力飽和電圧まで増加してしまいます。そこで、コンデンサ$C_1$にシャント抵抗$R_2$を並列接続することによって、入力信号の交流成分は積分回路の動作、直流成分は反転増幅回路の動作をするように分類します。

交流成分と直流成分の境界は式(２)のカットオフ周波数が目安になります。

$$f_{c} = \frac{1}{2\pi R_{2}C_{1}} \tag{2}$$

入力信号の周波数を$f_{0}$とすると
$f_0 \gg f_c$: 交流信号（積分回路として動作）
$f_0 \ll f_c$: 直流信号（反転増幅回路として動作）

続いて、シャント抵抗が出力電圧に与える影響について考えます。図２の回路の伝達関数は式(３) のように表されます。

$$-\frac{1}{R_1} \times \frac{1}{\frac{1}{R_2} + sC_1} \tag{3}$$

式(３) より、シャント抵抗の影響のある$1/R_2$の項は$sC_1$よりも十分小さければ無視できる、そうでなければ無視できないということがわかります。あくまで目安ですが、$R_2$は$R_1$の10倍程度にすれば、出力電圧への影響は無視できることが多いです。

素子の値の決め方

$R_1$、$R_2$、$C_1$の値の決め方を、振幅1.5V、100kHzの方形波交流信号を積分回路で三角波に変換する回路を例に紹介します。

はじめに、出力電圧のゲイン$V_{out}/V_{in}$を決めます。入力信号と同じレベルにするためには$V_{out}/V_{in}=2$なります。（三角波の$V_{out}$はピークtoピークであるため）

続いて、$V_{out}/V_{in}$と積分時間から$R_1$と$C_1$の値を決めます。
積分時間は周期の1/2であるため、

$$\frac{T}{2} = \frac{1}{2} \cdot \frac{1}{f} = \frac{1}{2} \cdot \frac{1}{100 \times 10^3}=5\mu s$$

よって、

$$C_{1}R_{1} = \frac{V_{in}}{V_{out}} \cdot \frac{T}{2} = 2.5 \times 10^{-6}$$

$C_1$の容量を220pFに決めると、$R1$は11.4kΩ、大体12kΩとなります。

$R_2$は$R_1$の10倍程度を目安にして100kΩとします。

シミュレーション

図３：積分回路シミュレーション結果

図３は以下の条件で積分回路のシミュレーションした結果です。

• オペアンプ
  • TL082
  • 電源電圧：+3/-3
  • 出力飽和電圧：+1.5/-1.5
• 入力信号（方形波）：
  • 周期：10us、
  • 振幅：+1.5V、-1.5V
• 素子
  • $R_1$：12kΩ
  • $R_2$：120kΩ
  • $C_1$：220pF

ヒステリシスコンパレータ

ヒステリシスコンパレータ

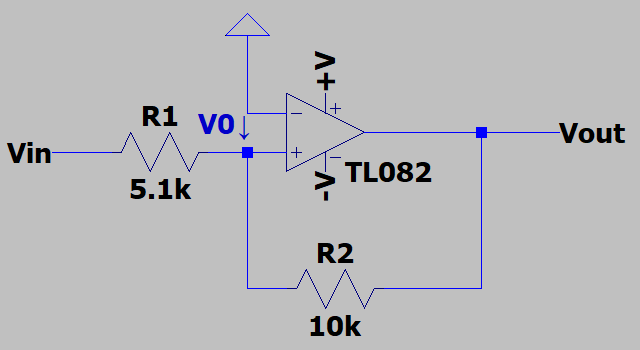
図４：ヒステリシスコンパレータ回路
図４はヒステリシスコンパレータ回路の例です。構造としては反転増幅回路のオペアンプの極性が反転した回路となっています。ヒステリシスコンパレータにおいて、バーチャルショートは成立しません。そのため、オペアンプの負極から正極にかかる電圧を$v_{0}$としたとき、式（４）が成り立ちます。

$$v_{0} = \frac{R_1}{R_1 + R_2} (v_{out} - v_{in}) + v_{in} \tag{4}$$

$v_{in}$が変化して、$v_{0}$の極性が反転すると、$v_{out}$は反転します。このとき、$v_{in}$による$v_{out}$の反転閾値は$v_{out}$自身の値に依存します。例えば、オペアンプの出力飽和電圧を$V_{opmax}$/$V_{opmin}$とするとき、$v_{out}$が$V_{opmax}$ならば、反転閾値$V_{h}$は

$$V_{h} = - \frac{R_1}{R_2} V_{opmax} \tag{5}$$

$v_{out}$が$V_{opmin}$ならば、反転閾値$V_{h}$は

$$V_{h} = - \frac{R_1}{R_2} V_{opmin} \tag{6}$$

上式は$v_{0}$の極性が反転するタイミング、すなわち$v_{0}=0$のとき、それぞれの条件で式（４）の方程式を解いた結果です。閾値電圧$V_{h}$は入力電圧の履歴（ヒステリシス）により、異なることがわかります。

シミュレーション

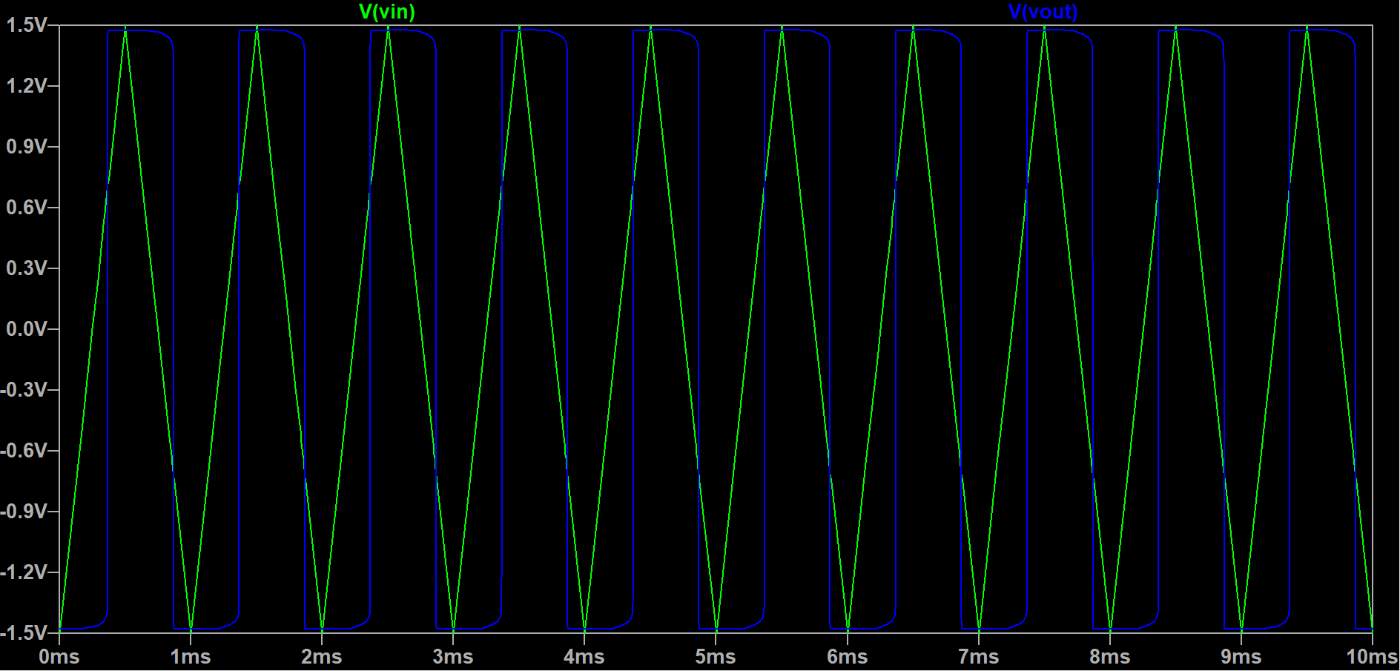
図５：ヒステリシスコンパレータシミュレーション結果１

図５は以下の条件でヒステリシスコンパレータのシミュレーションを行った結果です。

• オペアンプ
  • TL082
  • 電源電圧：+3/-3
  • 出力飽和電圧：+1.5/-1.5
• 入力信号（方形波）：
  • 周期：1ms、
  • 振幅：+1.5V、-1.5V
• 素子
  • $R_1$：5.1kΩ
  • $R_2$：10kΩ

上記の抵抗値より、$v_{out}$が$V_{opmax}$から$V_{opmin}$に反転する際の反転閾値$V_{h1}$は

$$V_{h1} = - \frac{5.1k}{10k} \times 1.5V = 0.765V$$

$v_{out}$が$V_{opmin}$から$V_{opmax}$に反転する際の反転閾値$V_{h2}$は

$$V_{h2} = - \frac{5.1k}{10k} \times -1.5V = -0.765V$$

となります。図５を見てみると、確かに三角波が0.765Vもしくは-0.765Vをまたぐタイミングで$v_{out}$が変化しています。

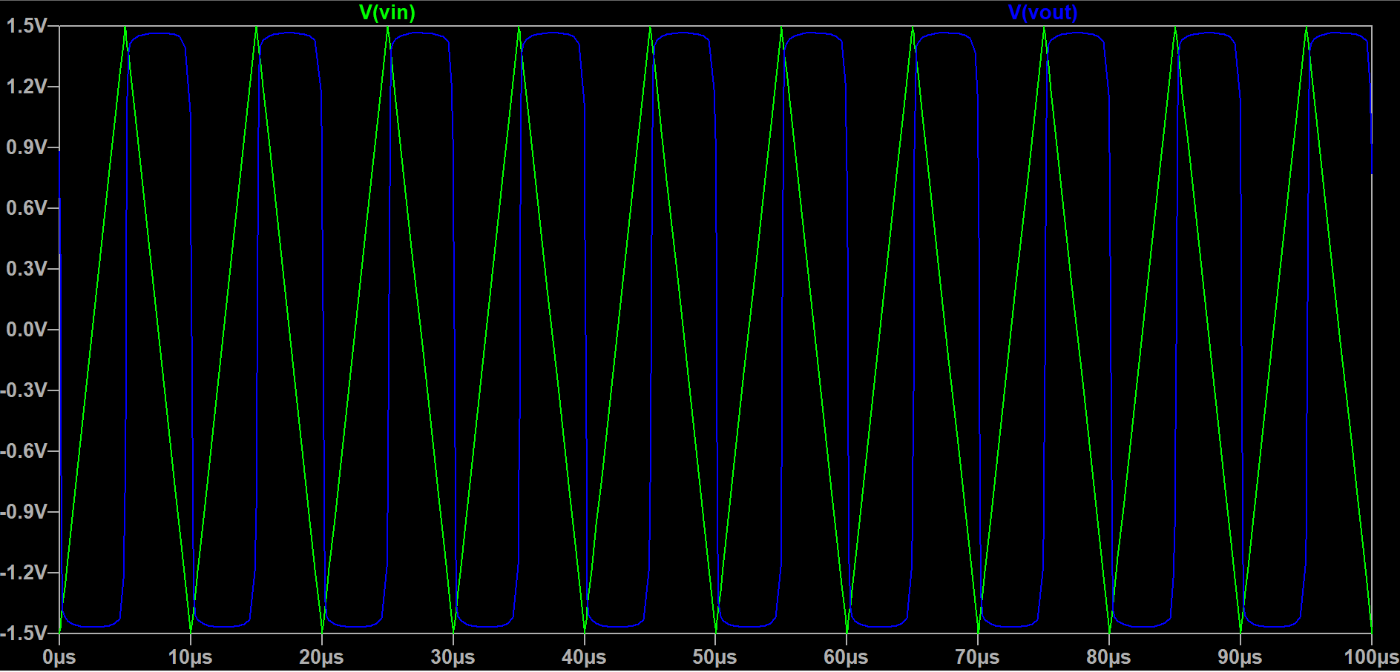
図６：ヒステリシスコンパレータシミュレーション結果２
図６は以下の条件でヒステリシスコンパレータのシミュレーションを行った結果です。

• オペアンプ
  • TL082
  • 電源電圧：+3/-3
  • 出力飽和電圧：+1.5/-1.5
• 入力信号（方形波）：
  • 周期：10us、
  • 振幅：+1.5V、-1.5V
• 素子
  • $R_1$：5.1kΩ
  • $R_2$：10kΩ

図６は図５の入力信号の周期を短くした（1ms->10us）場合の結果です。図６は三角波が閾値（+0.765/-0.765V）をまたぐタイミングと$v_{out}$が変化するタイミングが一致していません。

これはオペアンプの過負荷回復時間による出力電圧の遅延が原因であると考えられます（違うかもしれません）。そのため三角波に対して$v_{out}$が変化するタイミングは期待より遅延しています。一般的に過負荷回復時間が問題になるのはオペアンプの出力が最終的な振幅に達する前に入力信号が変化してしまう場合です。図６は三角波が次の閾値到達する前に$v_{out}$が最終的な振幅である$V_{opmax}$もしくは$V_{opmin}$に到達しているので生成される波形の形状的には問題ありません。

しかし、三角波生成回路に使用する場合は問題になります。三角波生成回路はヒステリシスコンパレータと積分回路がループした回路です。ヒステリシスコンパレータにおける遅延は積分回路における三角波の生成に影響を及ぼし、その三角波は自分自身の入力となります。結果として生成される三角波の周波数は意図したものより低くなります。高周波数を扱う場合は、オペアンプの代わりにコンパレータを使用するのが無難かもしれません。

三角波生成回路

三角波生成回路

図７三角波生成回路
図７は積分回路とヒステリシスコンパレータを組み合わせて生成した三角波生成回路です。左側がヒステリシスコンパレータ、右側が積分回路で、ヒステリシスコンパレータが出力した方形波が積分回路の入力信号に、積分回路の出力した三角波がヒステリシスコンパレータの入力信号となっています。

三角波の周期$T$は以下のように求められます。
時刻$t=0$における積分回路の出力が$v_{out}=V_h$であるとします。半周期後$t=T/2$の出力電圧は$v_{out}=-V_h$です。ヒステリシスコンパレータの出力飽和電圧を+V/-V、積分回路への入力電圧を$v_{in}$とするとき、以下の式が成り立ちます。

$$v_{out} = -\frac{1}{R_3 C_1}\int^{T/2}_{0}v_{in}dt + V_h = -\frac{VT/2}{R_3 C_1} + V_h = - V_h\\ T = \frac{4R_3 C_1 V_h}{V} \tag{7}$$

式（５）と式（７）より、周期$T$が求められます。

$$T = \frac{4 R_1 R_3 C_1}{R_2} \tag{8}$$

式（８）を用いて図７の回路が生成する三角波の周波数を求めてみます。
各素子の値は$R_1$：5.1kΩ、$R_2$：10kΩ、$R_3$：100kΩ、$C_1$：220pFより、

$$T = \frac{4 \times 5.1k \times 100k \times 220p}{10k} = 44.88us$$

周期44.88us、つまり約22kHzの三角波が生成されることがわかります。

シミュレーション

図８：三角波生成回路シミュレーション結果１

図８は以下の条件で三角波生成回路のシミュレーションを行った結果です。

• オペアンプ
  • TL082
  • 電源電圧：+3/-3
  • 出力飽和電圧：+1.5/-1.5
• 素子
  • $R_1$：5.1kΩ
  • $R_2$：10kΩ
  • $R_3$：100kΩ
  • $C_1$：220pF

三角波の振幅と周波数はおおよそ理論値と一致しています。しかし、振幅は理論値である1.53V（+0.765/-0.765V）よりも若干大きく、周波数も理論値の22kHzよりも若干小さい20kHzとなりました。これはヒステリシスコンパレータのシミュレーションで考察した過負荷回復時間が原因であると考えられます（違うかもしれません）。

実装

図９：三角波生成回路の実験の様子
図９は左から、電源回路、三角波生成回路、オシロスコープです。電源回路ではDC6Vをバッテリ・スプリッタ回路で3Vずつに分圧しています。電源の実測値は$+V$：3.08、$-V$：-3.08Vとなりました。三角波生成回路は図７の回路を実装したものです。各素子の実測値は$R_1$：5.10kΩ、$R_2$：9.79kΩ、$R_3$：99.50kΩ、$R_4$：1.00MΩでした。静電容量を計測する機器がなかったため$C_1$の容量は測れませんでした。

図１０：オシロスコープの表示
図１０はオシロスコープの表示をズームしたものです。周波数は19.574Hz、波形の最大値は1.09V、最小値は-1.21V、波形全体は-0.06Vオフセットしています。振幅は理論値より大きく、周波数は理論値より小さくなりました。また、三角波はきれいな左右対称の三角形ではなく、上凸の頂点が本来よりも右に寄っています。

振幅と周波数の実測値が理論値とずれている現象は素子の実測値が理論値と異なることやオペアンプの過負荷回復時間が原因であると考えられます（違うかもしれません）。三角波が左右非対称になった原因は調査中です。わかり次第追記しようと思います。

まとめ

LTspiceによるシミュレーションと実際の回路制作を通じて三角波生成回路への理解を深めることができました。実際にやってみないとわからないことってたくさんあるんですね。

参考

• パワーエレクトロニクスノート―工作と理論
• 『積分回路』を分かりやすく解説！【オペアンプ】
• 積分回路
• 改良された積分回路
• 積分回路 - オペアンプ
• シャント抵抗器（電流検出抵抗器）とは？
• 入力オフセット電圧
• コンパレータのヒステリシス設定について
• LTSpice使い方講座「電源Voltage/Current」の設定方法
• オペアンプをコンパレータとして使用する際のヒント