🔼

【Python】パスカルの三角形

2023/06/18に公開

Python

初心者

アルゴリズム

tech

はじめに

ブループロトコルサービス開始日はログインできませんでした。キョです。

今回は「フィボナッチ数列」の続きに、
「パスカルの三角形」の実装を行いたいと思います。

パスカルの三角形とは？

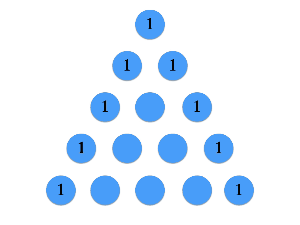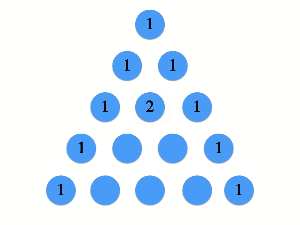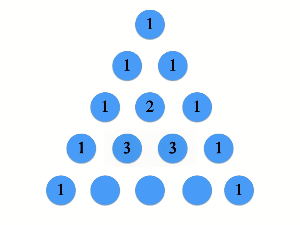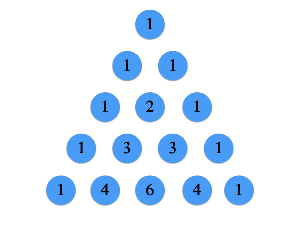
以下の画像のような三角形がパスカルの三角形になります。

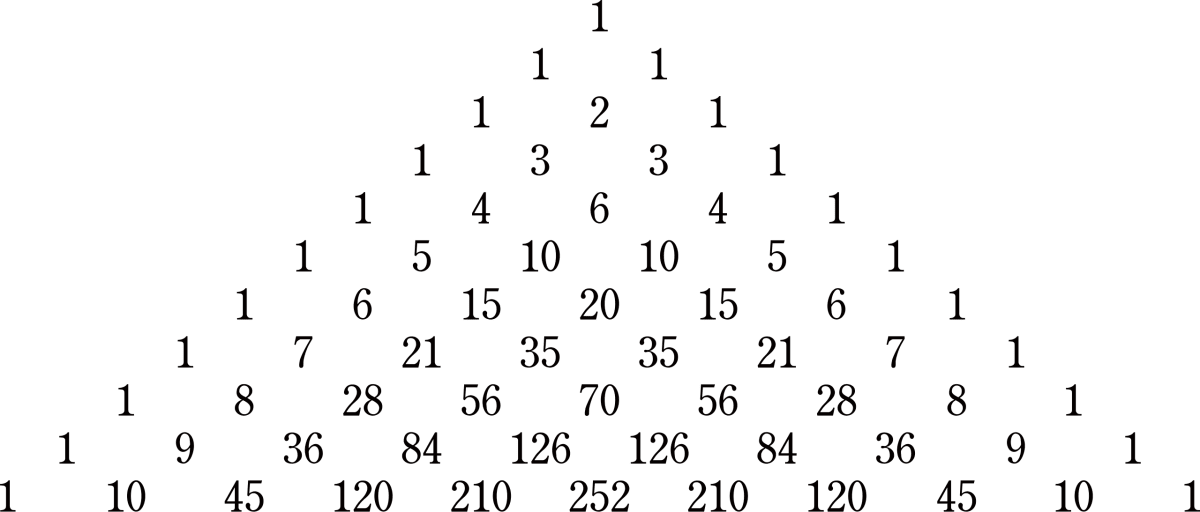
ルールはシンプルで、三角形の数値は

各行の一番左の数値は1
各行の一番右の数値は1
各行の他の数値 = 自分の左上の数値 + 自分の右上の数値

です。

以下のサイトから引用したgif図を見ればイメージやすいと思います。
パスカルの三角形Gif

Wikiの説明は以下になります。

パスカルの三角形は二項展開における係数を三角形状に並べたものです。

実装

上の画像のような三角形を出力するまでの実装ではなく、
二次元の配列を出力値とした実装を行いたいと思います。

例えば、高さが３のパスカル三角形の場合の出力値は下記になります。

[[1], [1, 1], [1, 2, 1]]

1.再帰による実装

今回もまず、再帰で実装していきます。

再帰で実装する時の考え方は、フィボナッチ数列と同じ感じになります。
各行の各値を計算する対象として、下のルールに沿って、実装します。
※二項係数を計算していくイメージですね。

各行の一番左の数値は1
各行の一番右の数値は1
各行の他の数値 = 自分の左上の数値 + 自分の右上の数値

コードは以下になります。

from typing import List
from sys import argv

# 二項係数を求める関数
def c(n,k: int) -> int:
    if k == 0 or k == n:
        return 1
    else:
        return c(n-1, k-1) + c(n-1, k)

# パスカルの三角形を求める関数
def pascal_triangle(n: int) -> List[List[int]]:
    triangle = []
    for depth in range(n):
        row = []
        for i in range(depth + 1):
            row.append(c(depth, i))
        triangle.append(row)
    return triangle

if __name__ == '__main__':
    if len(argv) > 1:
        print(pascal_triangle(int(argv[1])))
    else:
        print('no argument')

試しに高さ5のパスカルの三角形を計算してみましょう。

$ python PascalTriangle.py 5
[[1], [1, 1], [1, 2, 1], [1, 3, 3, 1], [1, 4, 6, 4, 1]]

問題なさそうですね。

2.for文による実装

再帰の実装を見ると気づくかと思いますが、
実はc関数の実装は二次元配列の操作で、for文だけでも実装できますね。
さっそく実装してみましょう。

from typing import List
from sys import argv

# パスカルの三角形を求める関数
def pascal_triangle(n: int) -> List[List[int]]:
    triangle = []
    for depth in range(n):
        row = []
        for i in range(depth + 1):
            # c関数の処理をここで行う
            if i == 0 or i == depth:
                row.append(1)
            else:
                row.append(triangle[depth-1][i-1] + triangle[depth-1][i])
        triangle.append(row)
    return triangle

if __name__ == '__main__':
    if len(argv) > 1:
        print(pascal_triangle(int(argv[1])))
    else:
        print('no argument')

これだけで実装完了ですね。
高さ5のパスカルの三角形を計算してみます。

$ python PascalTriangle.py 5
[[1], [1, 1], [1, 2, 1], [1, 3, 3, 1], [1, 4, 6, 4, 1]]

事前にすべての値が全部1になる二次元配列を用意すれば、
判断部分をなくしてもいいなので、これも実装してみます。

from typing import List
from sys import argv

# パスカルの三角形を求める関数
def pascal_triangle(n: int) -> List[List[int]]:
    triangle = [[1] * (i + 1) for i in range(n)]
    # 1行目と2行目は計算不要なので飛ばす
    for depth in range(2, n):
        # 1列目と最終列は計算不要なので飛ばす
        for i in range(1, depth):
            triangle[depth][i] = triangle[depth-1][i-1] + triangle[depth-1][i]
    return triangle

if __name__ == '__main__':
    if len(argv) > 1:
        print(pascal_triangle(int(argv[1])))
    else:
        print('no argument')

高さ5のパスカルの三角形を計算してみます。

$ python PascalTriangle.py 5
[[1], [1, 1], [1, 2, 1], [1, 3, 3, 1], [1, 4, 6, 4, 1]]

3.個人的に一番好きな実装方法

パスカルの三角形の特徴を見ると、わかったのは、

ある行の値を全部計算するためには、計算したい行の上の行の値が必要

です。
なので、個人的に一番わかりやすいと思う実装方法は以下になります。

from typing import List
from sys import argv

# 1行分のパスカルの三角形を求める関数
def create_next_row(row: List[int]) -> List[int]:
    # 1行目は1を返す
    if len(row) == 0:
        return [1]
    # 2行目は1,1を返す
    elif len(row) == 1:
        return [1, 1]
    # 3行目以降は、1, n-1行目の値の和, 1を返す
    else:
        return [1] + [row[i] + row[i+1] for i in range(len(row)-1)] + [1]

# パスカルの三角形を求める関数
def pascal_triangle(n: int) -> List[List[int]]:
    triangle = []
    for i in range(n):
        triangle.append(create_next_row(triangle[-1] if triangle else []))
    return triangle

if __name__ == '__main__':
    if len(argv) > 1:
        print(pascal_triangle(int(argv[1])))
    else:
        print('no argument')

高さ5のパスカルの三角形を計算してみます。

$ python PascalTriangle.py 5
[[1], [1, 1], [1, 2, 1], [1, 3, 3, 1], [1, 4, 6, 4, 1]]

最後に

三つの方法で実装してみました。
やっぱり個人的にはわかりやすいほうが一番いいかと思いますね。
みなさんもぜひ自分で実際に実装してみてください。

それでは、良い開発ライフをお送りください。