🤖

最適制御のモデル、評価関数をsympyで実装、実行する

2024/04/20に公開

Python

sympy

モデル予測制御

tech

モデル予測制御に関する勉強ノートを兼ねています。

モデル予測制御

制御入力u(t)が加わりある微分方程式(状態方程式)に従って運動する対象x(t)に
$\dot{x}=f(x,u,t)$
においてコスト関数(評価関数)
$J=\phi(x(t_T))+\int_{t_0}^{t_T}L(x(t),u(t),t)dt$
を最小化するように制御変数uを決定するのが最適制御問題でありその中でも現時点から一定期間後のxの値とその間のコスト関数の最小化を各時間ステップで行う問題をモデル予測制御といいます。コスト関数を評価する期間をホライズンと呼びます。

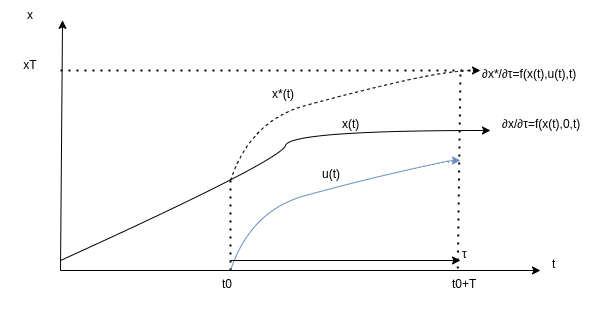
期間t0~t0+Tの間制御入力uを加えられた軌道x*(t)と時刻t0+Tでの目標値xT

状態方程式f(x(t),u(t),t)、評価関数J(x(t),u(t),t)が与えられたときに状態方程式を満たさなければいけないという高速条件から随伴変数λを加えたハミルトニアンH(x,u,λ,t)=J(x(t),u(t),t)
が定義されJの変分δJの各変数に関する係数が0になることからオイラー・ラグランジュ方程式
$\dot{x}=f(x,u,t)$
$x(t_0)=x_0$
$\dot{\lambda}=-\frac{\partial H}{\partial x}^T$
$\lambda(t_T)=-\frac{\partial \phi}{\partial x}^T(x(t_T))$
$\frac{\partial H}{\partial u}=0$
が成り立つことになります。特にモデルが線形、目的関数が2次形式の場合(LQ制御)にはその係数はリカッチ方程式を満たすことが知られています。一般には非線形なのでオイラー・ラグランジュ方程式を満たすようなx(t),u(t),λ(t)を計算しなければいけません。まずu(t)を未知とするのが自然でこの場合にはx,λに関する微分方程式を初期値、目的地(終端値)から解いてそこから各時刻の $\frac{\partial H}{\partial u}$ を求めて0とのズレの分だけ勾配法やニュートン法でuを修正するという方法になります。これとは別にλを未知とする方法があります。この場合は終端条件の誤差 $\lambda(t_T)-(\frac{\partial \phi}{\partial x})^T(x(t_T))$ から勾配を求めてλの初期値λ0を変えていく方法でありシューティング法と呼ばれます。

CGMRES法について

モデル予測制御ではホライズンの間だけ微分方程式を解く必要がありその期間は時々刻々と変化します。
その期間の間のズレ $\frac{\partial H}{\partial u}$ を並べた量
$F(U(t),x(t),t):=[\frac{\partial H}{\partial u}(x(t_0),u(t_0),\lambda(t_0),t_0),\frac{\partial H}{\partial u}(x(t_1),u(t_1),\lambda(t_1),t_1),...,\frac{\partial H}{\partial u}(x(t_T),u(t_T),\lambda(t_T),t_T)]$
を考え、これが時間とともに0に収束するような条件
$\frac{d}{dt}F=\zeta F$
$\frac{\partial F}{\partial U}=-\zeta F-\frac{\partial F}{\partial x}\cdot{x}(t)-\frac{\partial F}{\partial t}$
を課せば制御は安定することになります。Fに関する各偏導関数を数値的に求めればこれは
ベクトル $U(t):=[u(t_0),u(t_1),...,u(t_T)]$ の時間微分 $\cdot{U}$ に対する線形の連立方程式を解く問題に帰着されます。「非線形最適制御入門」
ではこれをArnordi法で解いておりCGMRES法と呼ばれています。

実装

CGMRES法のpython実装に関しては以下のブログを参考にさせていただきました。
非線形モデル予測制御におけるCGMRES法をpythonで実装する
 C/GMRESシミュレーションを3つの言語で作ったので比較してみた
 C/GMRES法の例題実装

上記の実装ではControllerのクラス内で特定のモデルの状態方程式f(x(t),u(t),t)、ハミルトニアンH(x,u,λ,t)の偏導関数 $\frac{\partial f}{\partial x},\frac{\partial f}{\partial u},\frac{\partial H}{\partial x},\frac{\partial H}{\partial u},\frac{\partial H}{\partial x_T}$ をpython,numpyの関数として直接定義しています。sympyを使えばf,Hの関数形を与えるだけで偏導関数を手で実装することなく自動で計算し、numpyに変換してくれるようになります。これによって非線形モデル予測制御におけるCGMRES法をpythonで実装するで挙げられたモデル予測制御の難点"随伴方程式や最適性行列Fを手計算で算出する必要があり，ハンドメイド的な解法が必要"を解決することができます。Controllerクラスの関数はxの予測計算Foward,λの計算Backward,Fの計算、CGMRES法本体と簡潔になります。
実は上記の大塚先生がMathematicaの書式で書いた数式からC言語のコードを自動生成するAutoGenUというプログラムを作成されています。

sympyではまず変数を

で定義し、その変数や定数を使った行列、ベクトル値関数を

などで定義します。

でグループ化した変数(ここではu)に対しHの偏導関数 $\frac{\partial H}{\partial u}$ は

と書かれます。偏導関数のnumpy化は

sp.lambdify((xs,u), Hu,"numpy")

という関数で成されます。

lambdastr((xs,u),Hu)

とすると変換された関数の定義を見ることができます。

実は3次元のgradient,divergenceはsympyのCoordSys3Dモジュールを用いればわかりやすく書くことができます。

しかしnumpyへの変換が若干面倒なことと

一般に工業プラントやエンジンなどの実例では制御対象、制御変数は3次元以上であるのでここでは用いませんでした。

計算結果

当然ですがもともとのコードと結果は一致します。ただし実際の計算時間は初期化時のnumpy関数への変換を除いてももとのコードに比べて増大してしまいました。これはもともとForward処理で計算した $\partial f/\partial u$ を $\partial H/\partial u$ の計算で再利用していたものを逐一計算するようにしてしまったためです。2輪車モデルの場合の計算の結果のグラフ、計算時間はnotebook
に記しました。Jupyter notebookではsympyの行列を含む数式をレンダリング表示することができます。「非線形最適制御入門」のモデルはこちらです。モデルfとハミルトニアンHを変えることでコントローラーは完全流用できることがわかります。

こちらの実装ではモデル側が導関数を実装しそれを制御アルゴリズムがようなインターフェースにすることで様々な力学モデルと制御アルゴリズムの組み合わせを実現しています。

sympyでバンドルアジャストメントを書く！

本

可観測性、リッカチ方程式の導出、ｚ変換などの基本やインパルス応答、ステップ応答をつかって対象をモデリングする方法、参照機能の目標への近づけ方、制約の入れ方などの制御理論のお約束や周波数空間で見る古典制御と現代制御の対応などがわかりやすく書かれています。モデル予測制御の話は「非線形最適制御入門」と重なりますがより実践的です。

「非線形最適制御入門」でのオイラーラグランジュ方程式の導出に相当するところはなく、安定性、ロバスト制御などの話題も含み高度に感じられます。制御理論は一定期間の時系列を用いた最適化問題であるのでそのアルゴリズムの解説も必要なのですが十分ではなく他の本を参照する必要が有ります。難解なのですが訳者の足立先生が書かれた上の本を読むと入りやすいです。

モデル予測制御

CGMRES法について

実装

計算結果

本

Discussion