パラメーター空間の数え方と汎化(と特異学習理論)

最初に

joisinoさんのブログ
https://joisino.hatenablog.com/entry/theory
に基づきヘフディングの不等式とPac-Bayesの不等式復習の後にニューラルネットへのPac-Bayesの適用時に仮説空間(パラメーター)をどのように数えるべきかについて考察する。
Deep Learning is Not So Mysterious or DifferentのKolmogolov複雑性、Solomonoff事前分布を使った理想的な定式化と問題意識、そしてそれが特異学習理論とどう関係するのかについても記していきたい。

目標

帰納バイアスの少ないDNNの汎化性能が比較的高い直感的理由をPac-Bayesに基づいて示したい。

Pac-Bayesの復習

https://ludu-vorton.hatenablog.com/entry/2019/06/06/073000
https://seetheworld1992.hatenablog.com/entry/2017/06/04/150253
集中不等式の一種であるヘフディングの不等式
$Pr[\frac{1}{n}\sum_{i=0}^n (X_i-E[X_i])\le t)] \ge e^{-\frac{2n^2}{(a-b)^2}}$
$Pr[\frac{1}{n}\sum_{i=0}^n (X_i-E[X_i])\ge -t)]\ge e^{-\frac{2n^2}{(a-b)^2}}$

からのPac-Bayes不等式
$Pr [ R(h) \le \hat{R}(h) + \Delta \sqrt{ \frac{\log 1/P(h)+\log 1/\delta }{2n} }] \ge 1-\delta$
の導出はDeep Learning is Not So Mysterious or DifferentのAppendix Cが詳しい。以下に書く。

導出

天下り的だが任意のtに対するヘフディングの不等式
$Pr[R(h) \le \hat{R}(h)+t]=Pr[nR(h)\le n\hat{R}(h)+nt]$
$Pr[R(h) \le \hat{R}(h)+t] \ge \exp(-2nt^2/\Delta^2)$

で関数t(h)を$\delta$に対して
$exp(-2nt(h)^2/\Delta^2=Pr(h)\delta$
となるように取る。式変形すると
$t(h)=\Delta\sqrt{ \frac{\log 1/P(h)+\log 1/\delta}{2n} }$
となる(第2項)。一方学習データ[x]から作られた仮説$h^*([x])\in \mathcal{H}$
$\hat{R}(h^*)=\sum{i=1}^n R(h^*([x]),x_i)$
に対しても
$R(h^*)\le R(h^*)+t(h^*)$

と書くことができる。$\bigcup_{h\in \mathcal{H}} [R(h) \ge \hat{R}(h)+t(h)]$にヘフディングの不等式を適用し
$Pr[R(h^*) \ge \hat{R}(h^*)+t(h^*)] \ge Pr[\bigcup_{h\in \mathcal{H}} [R(h) \ge \hat{R}(h)+t(h)]]$
$\ge \sum_{h\in \mathcal{H}} Pr[ R(h) \ge \hat{R}(h)+t(h)]$
$\ge \sum_{h\in \mathcal{H}} Pr(h)\delta=\delta$

$t(h^*)$に先程の
$t(h)=\Delta\sqrt{ \frac{\log 1/P(h)+\log 1/\delta}{2n} }$を代入すればPac-Bayes
不等式
$Pr [ R(h) \le \hat{R}(h) + \Delta \sqrt{ \frac{\log 1/P(h)+\log 1/\delta }{2n} }] \ge 1-\delta$
が得られる

(cf 集中不等式ごとに非平衡統計力学が定義できるのかもしれない(先行研究あり))

幾何学的意味付け

Pac-Bayes不等式の中身
$R(h) \le \hat{R}(h) + \Delta \sqrt{ \frac{\log 1/P(h)+\log 1/\delta }{2n} }$
はloss関数の谷(底)の部分の深さが$\hat{R}$,幅が第2項$\Delta$で書かれその和が汎化能力（の上限）を与えているとみることができる。分布は入力データがある分布関数にに従っていてランダムにSGDに影響するため幅を持っている。
図示すると”狭くて深い谷”は汎化能力が低く、”浅くても広い盆地”のほうが汎化性能が高くなることが有りえ、データ数Nによってそれが異なる(同様の描像が特異学習理論に置いてもできるが、そこでは谷の平らさではなく特異性が指標となる)。　

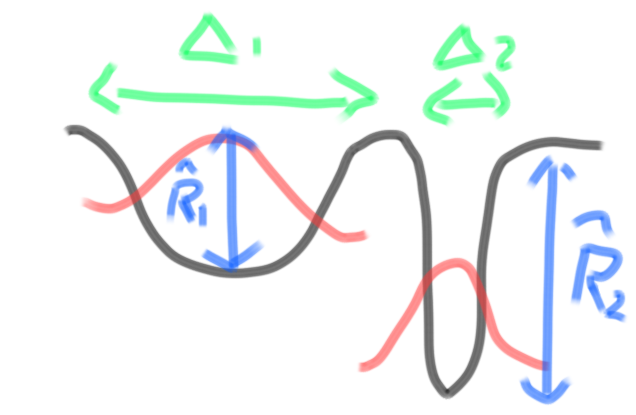
図矢印の長さの逆数が$\hat{R},\Delta$の値

数え上げによるパラメータ空間内の点(仮説)の評価

https://joisino.hatenablog.com/entry/theory

Pac-Bayesの式に従えば　最も簡単(第0次的)には盆地全体が1つの仮説とみなせることになる。
さらに全ての鞍点は大域最適解につながっていると仮定できれば話は単純だが、そうでなければ初期値がランダムであるという事前分布のもとで各局所最適解(固定点アトラクタ)のベイシンが仮説空間の体積となり、汎化性能と言える。
二次の係数を見ればFisher情報量、情報幾何的な見方になる。情報量基準(特にBIC)との関係も参考になるが、完全に対応しているわけではなく、幾つかの変種が存在する。
(論文紹介スライドの17ページでも紹介している。)

圧縮と汎化

Transformer as RNN

トランスフォーマーは重み$w_n$を状態としたRNNです
この「圧縮」と「汎化」と「効率」の関係はモデルの振る舞いを考えるうえでとても重要です。トランスフォーマーを RNN として見ることで、圧縮度合いを状態の次元数という形で陽に表すことができるようになり、この三者関係を意識的に取り扱えるようになるという点でも、この見方を身に付けることは有用です。

と言える。如何にして圧縮は帰納的バイアスなしに行われているのだろうか？
また圧縮とは実際には高次元空間に分布するデータを適切パラメータ表現できるに低次元(多様体)に分布しているがそれはどのように成されているのか。そのヒントは以下にある。

多様体仮説とNTKと幾何学

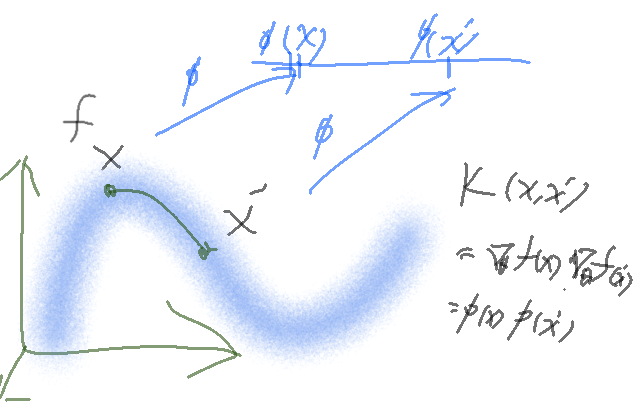
Neural Tangent Kernel(NTK)は関数fに対して
$K(x,x'):= <\nabla_\theta f(x) ,\nabla_\theta f(x') >$
と定義される。これによって高次元空間に埋め込まれたデータの低次元接空間だけを考えれば良くなる。

情報幾何における内積(Fisher information matrix)
$g_{ij}(\xi):=E_\xi [\frac{\partial}{\partial_{xi_i}}\log p(x,\xi) \frac{\partial}{\partial_{xi_j}}\log p(x,\xi)]$
$E_\xi[f(x)]=\int f(x)p(x|\xi)dx$ とxが積分されパラメーター$\xi$が残るので座標が異なる。
https://medium.com/lsc-psd/neural-tangent-kernel-ntk-の概要-faf0ad249923

この圧縮機構にはコンピューターサイエンス、業界でより一般的に使われるzipやエントロピー符号化のようなデータ圧縮も含むのだろうか。Kolmogolov複雑性は後者の概念を含んでいる。ちょっと苦手そうではあるもののLLM,Transformerが自然言語やプログラミングでの質問をある程度適切に処理できる現状を鑑みるに一般のデータ圧縮も含まれるようだ混合ガウス分布の塊の個数を学習させるのが実験として簡単だし容易い。

joisinoさんのブログのヒント

データの性質によってカーネルや圧縮度合いを選択することができます。例えば、テキストは離散的であり、各トークンの粒度が大きく、少しでもトークンを忘れてしまうと将来の応答で問題が生じる可能性があります。よって、テキストではあまり圧縮は行わず、従来のトランスフォーマーのような無限次元やそれに近い状態空間を用いて、入力をほとんどそのままの形で記憶すると良いと考えられます。一方、動画や音声は連続的であり、一部のフレームをが抜け落ちても問題なく、かなりの程度圧縮ができるので、そのような場合にはより RNN 的な、圧縮率の高い、次元の低い状態空間を用いて、圧縮しながら処理すると良いと考えられます。同じドメインの中でも、分布やタスクの性質によって、どの程度まで圧縮できそうかを考えてこのスペクトルの中の位置を決めることができます。

「Deep Learning is Not So Mysterious or Different」
https://docs.google.com/presentation/d/1TLnCElJZAcqm3ZK8ANj3iHNT8-OXl1MHJysPhEto1MI/edit?slide=id.g36b072f2857_0_18#slide=id.g36b072f2857_0_18

ではPac-Bayesの式の事前分布に連続値を用いたパラメータ空間はRademacher Complexityを用いた数え方では捉えきれずPac-Bayesの誤差上界は圧縮されたパラメーター空間で表現されるとしている。

Kernel法についての解説

特異学習理論とは結局関係するのか

以上のようにベイズ的な意味での解の安定性、性質の良さを実際に学習されたネットワークのHessianのランク、行列式、固有値(0固有値)を見るのが早い。有効次元という概念はHessianの非零固有値の比率$N_{eff}:=\sum_i \frac{\lambda_i}{\lambda_i+\alpha}$(αは定数)と言えるが特異学習理論ではそれでは不十分としている。
(Hessianの0固有値の数は高次元特異点の安定性に関係するかもしれないという期待、関連研究[要出典]ChatGPT5の意見。)

https://arxiv.org/abs/2308.12108
では実対数閾値(RCLT, 学習係数、λと書く)の局所解(λ*)について数値的に求め、厳密解が求められる線形深層ネットワーク(行列分解モデル) のλとλ^の比較を示している。
$\hat{\lambda}(w^*):=$$n\beta^*[ E_{w|w^*,\beta^*,\gamma}L_n(w)−L_n(w^*)]$
$\lambdaˆ_{SGLD}(w^*):=n\beta^*[\frac{1}{T}\sum^T_{t=1} L_n(wt)−L_n(w*)]$

PAC-Bayesとの類似性も論じられている。
$\lambda_{PAC−bayes}(w^∗)=E_{q(w|w∗)}ℓ_n(w) − ℓ_n(w^∗)$

技術的にはSGLD(確率降下ランジュバン)とMALA(Metropolis-adjusted Langevin dynamic)を用いている。そのあとNUTS MCMCや変分ベイズを用いたライブラリpyroで実装している。
https://zenn.dev/xiangze/articles/2249f2221b0a5d

RLCT等代数的不変量間の関係に関するChatGPTの説明
https://zenn.dev/xiangze/scraps/c2d1601cc9edfe
https://chatgpt.com/share/68b42eb1-aacc-8008-b7c3-a7b7ab43e2d1

現時点で言えること

正則なモデルでは最適な(暗黙の)学習係数(BICのペナルティー項)は=パラメーター数、非正則なモデルでは直感的には(パラメーター数-Hessianの0固有値の数)になるが、特異モデルに関してはそうはならず一般には(パラメーター数-Hessianの0固有値の数)よりも小さな値になり、その度合いは実対数閾値("特異性の指標")によって異なる。
特異性の高いモデルのほうが学習係数(暗黙の帰納バイアス)が低いように思えるがCNN,Resnet,Transformer間での違いを算出、性質を説明できるだろうか。

その他の話題(未完)

Deep Learning is Not So Mysterious or Differentで触れられていた概念

データ、ネットワークの(連続)対称性が局所最適解(だったもの)、特異点をつなぎ、学習が進むに連れての遷移を用意にするという描像

Residual pathway priors、その実装との関係

https://arxiv.org/abs/2112.01388

mode connectivity

https://arxiv.org/abs/1802.10026

データ、ネットワークの対称性

https://zenn.dev/xiangze/scraps/1c81f631c46478

数値実験

大規模非線形DNNでの実対数閾値、その他代数的指標の数値的見積、分布を見る、厳密解へのヒント

大規模線形ネットワークの局所最適解の数値的評価
https://arxiv.org/abs/1810.07716
https://arxiv.org/abs/2308.12108