多重共線性をチェックする方法
はじめに
多重共線性は相関行列を見てもチェックすることはできない。そして Ridge や Lasso などの正則化付き線形モデルも多重共線性をどうにかしてくれるわけではない(これらの方法でどうにかなると思っている人はもうちょっと深く考え直したほうがよい)。
私も普段明示的にはチェックしていない。それはよろしくないと思ったので多重共線性チェッカーを作った。
仕組み的には VIF(variance inflation factor)による多重共線性チェックと同じことで、VIF を計算するだけなら statsmodel ライブラリの variance_inflation_factor でもできる。
今回作成したコードでは、どの変数とどの変数が多重共線性を持っているかの情報まで可視化できる。Google Colabで作成したサンプルは以下。
参考文献
多重共線性の定義
データの入力
で表すものとする。
で表記するものとする。多重共線性とは、あるベクトル
が成り立つことをいう。実際のデータでは入力に含まれるノイズの影響で上の式は完全には成立しないので、
を成り立たせたとき、誤差のデータセット全体に渡る平均
を最小化させることを考える。このとき、
多重共線性のチェック方法
多重共線性の定義
を適当に式変形すると
となる。ややこしい見た目をしているが、要するに変数
import numpy as np
from sklearn.linear_model import Ridge
from sklearn.metrics import r2_score
def collinearity_check(Xc, model=None, alpha=1.0, emph=False):
"""
Parameters
----------
Xc : np.ndarray(m, n)
Input data (each data stored in a row).
model
Regression model (default Ridge).
alpha : float
Hyper parameter of Ridge (default 1.0),
ignored if model is not None.
emph : bool
Emphasize the result by R2 score or not.
Returns
-------
rc : np.ndarray(n, n)
Regression coefficient, emphasized by R2 score if emph is True.
scores : np.ndarray(n)
R2 scores.
"""
if model is None:
model = Ridge(alpha=alpha)
m, n = Xc.shape
if n < 2:
raise ValueError()
# 戻り値
rc = np.empty((n, n)) # 回帰係数
scores = np.empty(n) # R2スコア
X = np.copy(Xc)
for i in range(n):
y = np.copy(X[:,i]) # 自分を他の変数で回帰させる
X[:,i] = 1 # 自分は多重共線性の定数項に対応させる
model.fit(X, y)
y_calc = model.predict(X)
score = r2_score(y, y_calc)
if score < 0:
# R2 スコアが 0 以下なら線形性なしとみなす
scores[i] = 0
rc[i] = 0
else:
scores[i] = score
if emph:
# 係数が大きくても R2 スコアが 0 に近ければ 0 になるように加工
rc[i] = model.coef_ * score
else:
rc[i] = model.coef_
X[:,i] = y
return rc, scores
デフォルトで Ridge にしたのは線形回帰が解けない場合でも解けるからである。Lasso でやったら本当に関係のありそうなやつだけ残してくれるのでは、と期待したが、Lasso は多重共線性を考慮するわけではなく「使用する変数の個数を絞ってください」という命令に忠実に従うだけであり、試してみたら本当に関係があるやつまで削りやがったので使わないほうがいい。
ハイパーパラメータのmodel に渡してやればいい。
Ridge 以外にも多項式回帰とかのモデルを作って渡してやれば、線形回帰よりも強い関係性を一応は抽出できるはずである。
ちなみに
で定義される値をトレランス(tolerance: 許容範囲)という。入力ノイズがあって
なぜかは知らないが、トレランスの逆数を取った
を VIF(variance inflation factor)というらしい。確かに予測誤差の「分散」みたいなものである
多重共線性の可視化
今回の可視化コードを通常の相関係数のプロットと比較しておく。
疑似データの生成
疑似データ X を生成する。実際に分析するときはこの X をお手元のデータに置き換えてもらえればよい。
このあと、どの変数に多重共線性があるのかを可視化するが「多重共線性があるインデックスの表示」には正解が書いてあるので、そこは最後に見ると楽しい。
疑似データの生成
import numpy as np
np.random.seed(0)
# データ数
m = 100
# データの次元数
n = 18
# 多変量ガウス分布(各変数独立)
mu = np.random.normal(0, 150, n)
Lam = np.diag(np.random.uniform(1.0, 100, n))
X_indep = np.random.multivariate_normal(mu, Lam, m)
# いくつを選んで多重共線性を付加するか
k = 5
# 多重共線性のある変数をいくつ追加するか
N = 2
# 多重共線性のある変数を作成する
def make_collinear_vals(X, k, N):
X_crop = X[:, -k:]
A = np.random.normal(0, 1, (k, N))
b = np.random.normal(0, 10, N)
return X_crop.dot(A) + b
# 多重共線性のある変数を付加
X_origin = np.concatenate([X_indep, make_collinear_vals(X_indep, k, N)], axis=1)
# 加法ノイズを加えて多重共線性が完璧には成り立たないようにする
X_origin += np.random.normal(0, 1e-1, (m, n+N))
# ひと目でわからないようにシャッフル
idx = np.arange(0, n+N, 1)
idx_shuffle = np.random.choice(idx, n+N, replace=False)
X = X_origin[:, idx_shuffle]
多重共線性があるインデックスの表示
print(idx[idx_shuffle >= n - k])
[ 0 2 3 9 13 14 18]
前処理
入力データは標準化しておくと可視化がうまくいきやすい。
from sklearn.preprocessing import StandardScaler
Xsc = StandardScaler().fit_transform(X)
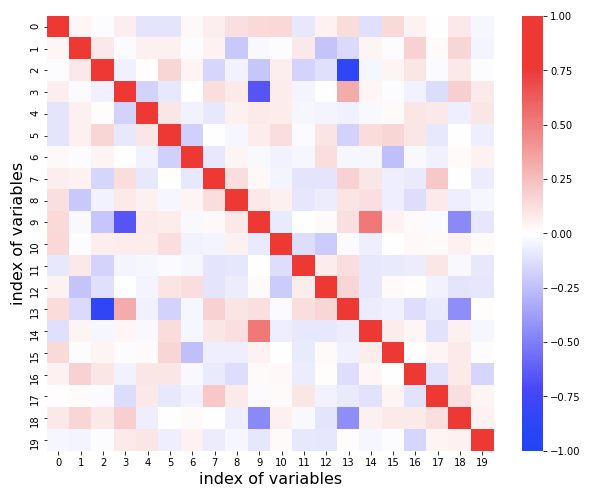
相関係数の可視化(よくない例)
相関係数だけで判断しようとすると痛い目を見るかもしれない。多重共線性がある変数はいくつで、どれなのかを読み取ろうとしてみるとよい。
from matplotlib import pyplot as plt
import seaborn as sns
import pandas as pd
plt.figure(figsize=(10,8))
sns.heatmap(pd.DataFrame(Xsc).corr(), vmin=-1, vmax=1, cmap='bwr', cbar=True)
plt.ylabel('index of variables', fontsize=16)
plt.xlabel('index of variables', fontsize=16)
plt.show()
今回作った可視化アルゴリズム
cc, cc_scores = collinearity_check(Xsc, emph=True)
# どの変数とどの変数に多重共線性があるのかを可視化する
from matplotlib import pyplot as plt
import seaborn as sns
import pandas as pd
plt.figure(figsize=(10,8))
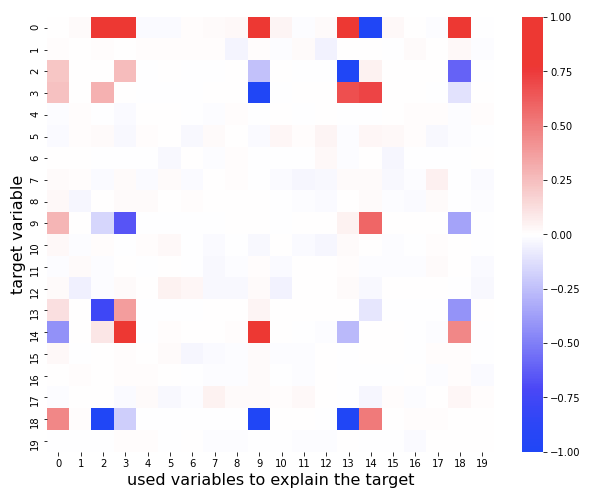
sns.heatmap(pd.DataFrame(cc), vmin=-1, vmax=1, cmap='bwr', cbar=True)
plt.ylabel('target variable', fontsize=16)
plt.xlabel('used variables to explain the target', fontsize=16)
plt.show()
このコードでプロットされる図はcollinearity_check関数を実行するときにemph=Trueを指定しておくと、重みに
# どの変数に多重共線性があるのかを可視化する
from matplotlib import pyplot as plt
plt.figure(figsize=(8,5))
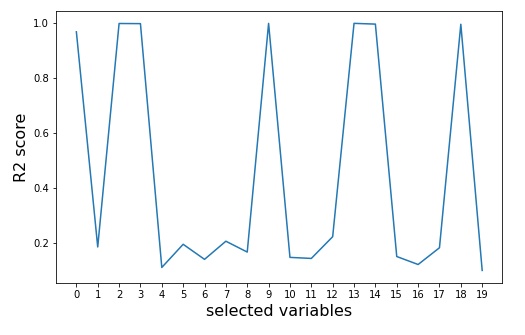
plt.plot(cc_scores)
plt.xticks(np.arange(0, len(cc_scores), 1))
plt.ylabel('R2 score', fontsize=16)
plt.xlabel('selected variables', fontsize=16)
plt.show()
このコードでプロットされる図は各変数を他の変数で回帰したときの
相関行列からは読み取れないだろうが、実は 0 番目の変数にも多重共線性がある。今回作成したアルゴリズムではかなり明確に読み取れている。
-
文献によって 5 以上と書いてたりするので適当だと思う。 ↩︎
Discussion