拝啓　厳しいガチャの冷え込みの中、冬のひだまりがことのほか暖かく

はじめに

ウマ娘は人格と呼べるくらいまで個々のキャラの個性が作り込まれているのでときどき見ている分には好きなコンテンツだ^[1]。さて、1st Anniversary だ、お祭りだ、ということでちょくちょく貯め込んでいた石を放出してみたが無料 10 連含めて 210 回引いて SSR は 3 枚。渋い。ウマ娘の SSR 排出率は 3% だが、私の感覚だと確率 3% は 30 回引けば 1 回当たるくらいのイメージなので、その半分以下は若干少ないんじゃあないか。私はどれだけ運が悪かったんだろう？

分析に用いたコードは以下。
https://colab.research.google.com/drive/1yVudbWZrjSM-Ctvg3w5VAs4ytTLLLAAc?usp=sharing

運の悪さを嘆くだけじゃつまらないから、邪悪なガチャの作り方も載せてあるよ！

ガチャの数理モデル

ソシャゲのガチャにはいろいろな種類があるが、単純化すると毎回の試行で「アタリ」か「それ以外」が出るモデルだと考えてよい。ウマ娘で言えば ☆3 を「アタリ」とした場合その排出確率は 3%、☆2 以下が「それ以外」で残りの 97% を占める。

「ガチャを$n$回引いたとき何回アタリが出るか」の確率は以下の二項分布でモデル化される。

$$\operatorname{Bin}(k|n,p) = {}_n C _ k p ^ k (1 - p) ^ {n - k}$$

$n$はガチャを引いた回数、$p$はアタリが出る確率、$k$はアタリが出た回数である。期待値は$np$なのでアタリ確率 0.03 で 100 回引けば

$$np = 100 \times 0.03 = 3$$

で大体 3 枚当たることになるから、30 回引けば 1 回当たるという私の感覚は若干楽観的ではあるものの概ね正しいことになる。ついでに二項分布の分散は$np(1-p)$である。期待値を計算したときと同じ条件であれば

$$np(1-p) = 100 \times 0.03 \times (1 - 0.03) = 2.91$$

である。二項分布は試行回数を増やしたとき正規分布でよく近似される^[2]ので、分散の平方根（正規分布であれば標準偏差）くらいは割と簡単にズレる。したがって

$$\sqrt{np(1-p)} = \sqrt{2.91} \fallingdotseq 1.7$$

より、1, 2 回くらいはアタリ回数がズレるということだ。つまり 100 回引いて 1 回しかアタリが出ないこともあれば、5 回くらいアタリが出ることもあるだろう、という感覚になる。

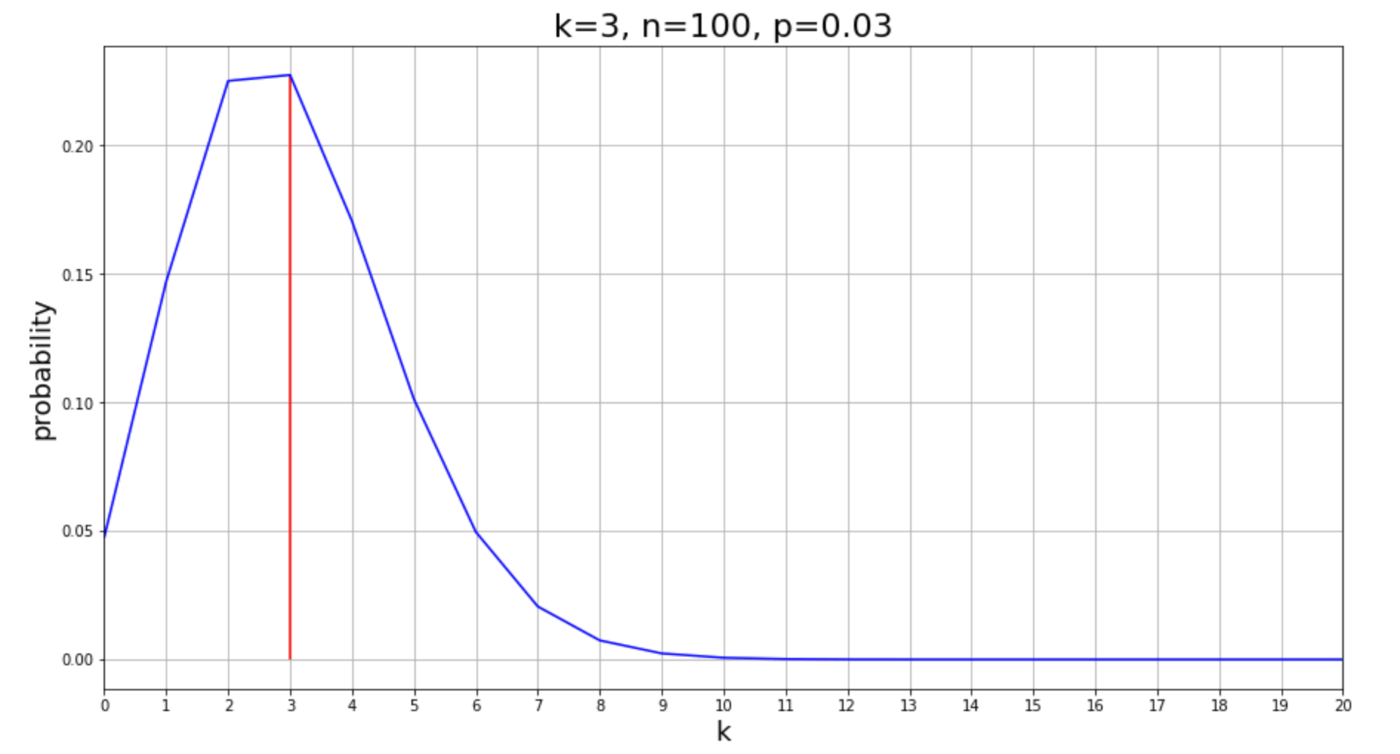
感覚ではなく厳密にどれくらいか、ということであれば二項分布の式に代入してみればよい。私の「アタリ 3% のガチャを 210 回引いて 3 回アタリが出た」が起こる確率を、Python の以下のコード

from scipy.stats import binom

print(binom.pmf(3, 210, 0.03))

で計算すると、

$$\operatorname{Bin}(k=3|210, 0.03) = 0.075$$

だから 7.5% くらいの確率である。おや？ けっこう低いな。でも TRPG のファンブルを引く確率よりは高いと思うと辛いけど否めない。ちなみに自分が分布のどの辺にいるのかを描画するコードは以下である。

import numpy as np
from matplotlib import pyplot as plt
from scipy.stats import binom

p = 0.03 # ガチャのアタリの確率

n = 100 # ガチャを引いた回数
k = 3 # アタリが出た回数

ks = np.arange(0, n+1, dtype=int)

pms = np.array([ binom.pmf(k, n, p) for k in ks ])

# 図のサイズ
plt.figure(figsize=(15, 8))

# 確率分布の描画
plt.plot(ks, pms, color='b')

# 自分がいる場所
plt.vlines([k], 0, binom.pmf(k, n, p), color='r')

# 適当に表示範囲を指定
plt.xticks(ks)
plt.xlim([0, 20])

# その他、図の描画設定
plt.grid(True)
plt.xlabel('k', fontsize=18)
plt.ylabel('probability', fontsize=18)
plt.title(f'k={k}, n={n}, p={p}', fontsize=22)

# 図を描画
plt.show()

ベイズ推定（腹いせ）

このガチャ渋すぎる！と思ったときはイカサマコインのベイズ推定を使って憂さ晴らしをするに限る。イカサマコインのベイズ推定は、最初に「コインの表裏が出る確率はともに$1/2$だよ」と伝えられたとき、コイン投げを繰り返して表裏の出る確率を見て「いや本当は$1/2$からこれくらい偏ってない？」と推定する方法である。ガチャに一般化すれば「アタリが出る確率は$x$だよ」 と伝えられたときに「いや本当は$x$からこれくらい偏ってない？」と推定できるわけである。

イカサマコインのベイズ推定では、アタリが出る回数$k$とアタリが出る確率$x$の同時確率分布を以下で定義する。

$$p(k, x) = p(k|x)p(x) = \operatorname{Bin}(k | n, x) \operatorname{Beta}(x | a, b)$$

ここで$\operatorname{Beta}(x | a, b)$は以下のように定義されるベータ分布である。

$$\operatorname{Beta}(x | a, b) = C _ B (a, b) x ^ {a - 1} (1 - x) ^ {b - 1}$$

ただし$C _ B(a, b)$は正規化定数である（計算に使わないので無視してよいが具体的にどう定義されているか気になれば各自調べてほしい）。

あとはベイズの定理を用いて、アタリが$k$回出たときのアタリが出る確率$x$の事後分布$p(x|k)$を推定すればよい。

$$p(x | k) = \frac{p(k, x)}{p(k)} \propto p(k, x)$$

第 1 辺から第 2 辺へはベイズの定理を用い、第 2 辺から第 3 辺へは$p(k)$が定数であることを用いた。記号$\propto$は比例記号であり、結ばれる両辺が定数倍の違いを除いて等価であることを意味する。計算を続行すると、

$$\begin{aligned} p(x | k) &\propto p(k, x) \\ &= \operatorname{Bin}(k | n, x) \operatorname{Beta}(x | a, b) \\ &= {}_n C _ k x ^ k (1 - x) ^ {n - k} \cdot C _ B (a, b) x ^ {a - 1} (1 - x) ^ {b - 1} \\ & \propto x ^ k (1 - x) ^ {n - k} x ^ {a - 1} (1 - x) ^ {b - 1} \\ &= x ^ {k + a - 1} (1 - x) ^ {n - k + b - 1} \\ & \propto \operatorname{Beta}(x | k + a, n - k + b) \end{aligned}$$

となることから、事後分布$p(x | k)$は事前分布と同じベータ分布$\operatorname{Beta}(x | \hat{a}, \hat{b})$になり、そのパラメータは

$$\hat{a} = k + a, \quad \hat{b} = n - k + b$$

と更新されることがわかる。

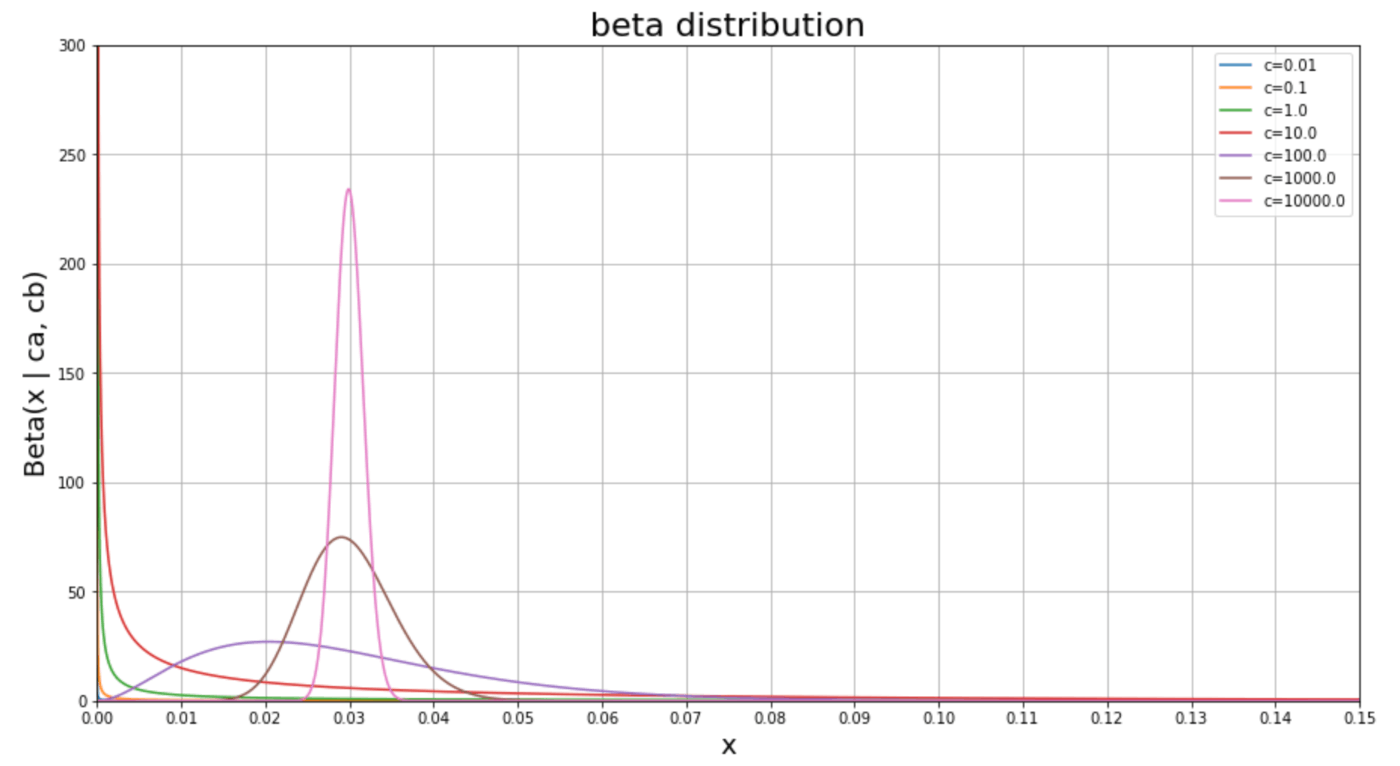
あとは事前分布を決めにいく。ベータ分布の期待値は

$$\frac{a}{a + b}$$

であり、分散は

$$\frac{ab}{(a + b) ^ 2 (a + b + 1)}$$

である。ガチャ詳細から今回アタリの確率は 3% のはずだから、

$$\frac{a}{a + b} = 0.03$$

となるように$a, b$を決める。これを満たすには$a:b = 0.03:0.97$が必要十分である。このようにして決めた$a, b$はそれぞれ$c$倍しても

$$\frac{ca}{ca + cb} = \frac{a}{a + b}$$

が成り立つから、$c$を適当に動かしてベータ分布の形状がどうなるかを見てみる。いま$a + b = 1$だから、$c$はおおまかには「事前知識が試行回数換算で何回分に相当すると仮定するか」に一致している。たとえば「ゲームに表示されている確率は、自分がガチャを 1000 回引いて確かめた確率と同じくらい信用に値する」と思うならば$c = 1000$を選べばよいし、あまり信用しないなら$c = 10$といった小さい値を選んでもよい^[3]。

import numpy as np
from matplotlib import pyplot as plt
from scipy.stats import beta

# ベータ分布のパラメータ
a = 0.03
b = 0.97

# ベータ分布の分散の調整
cs = np.logspace(-2, 4, 7)

# 確率変数
xs = np.linspace(0, 0.2, 10000)

# 図のサイズ
plt.figure(figsize=(15, 8))

# 確率分布の描画
for c in cs:
  plt.plot(xs, beta.pdf(xs, c*a, c*b), label=f'c={c}')

# 適当に表示範囲を指定
plt.xticks(np.arange(0, 1, 0.01))
plt.xlim([0, 0.15])
plt.ylim([0, 300])

# その他、図の描画設定
plt.grid()
plt.legend()
plt.title('beta distribution', fontsize=22)
plt.xlabel('x', fontsize=18)
plt.ylabel('Beta(x | ca, cb)', fontsize=18)
plt.show()

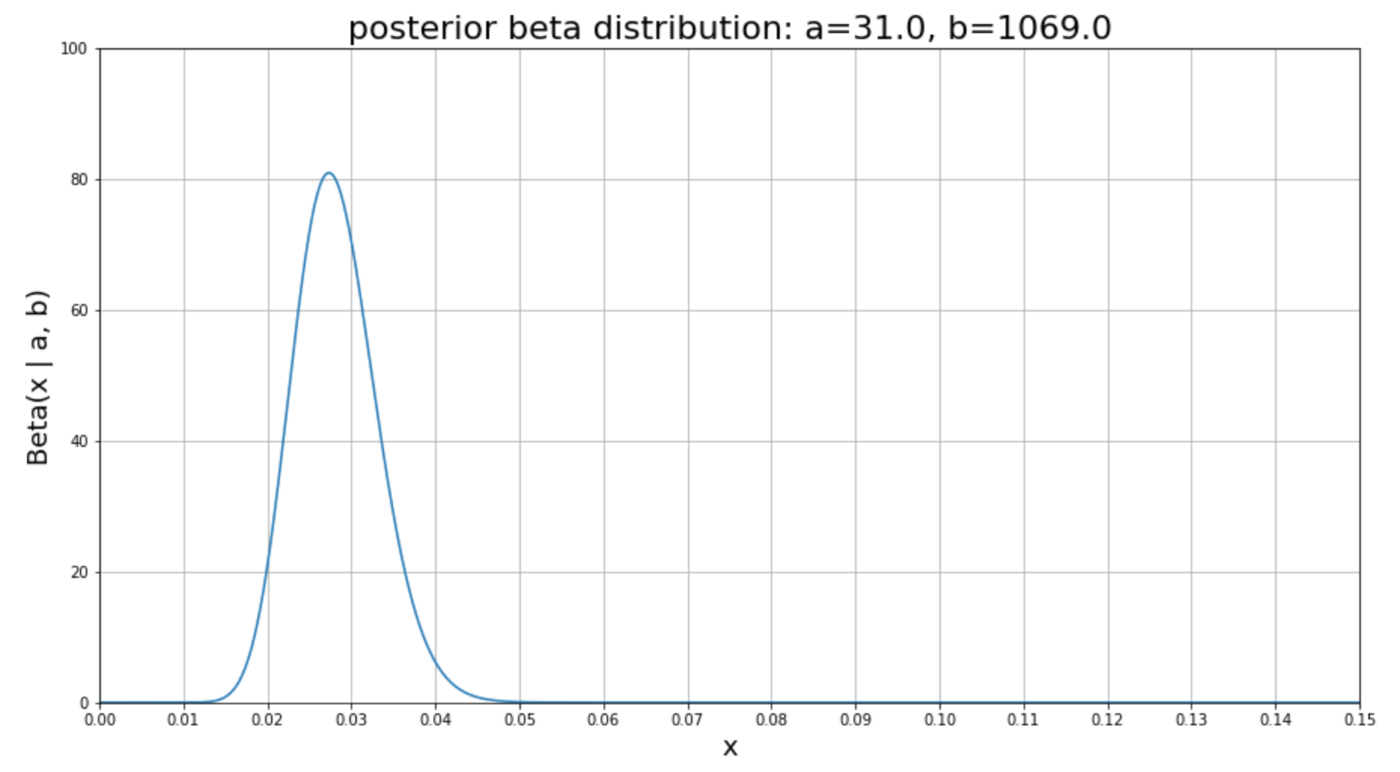
あとは式に代入するだけである。たとえば 100 回引いて 1 回しかアタリが出なかったとき、$c=1000$ならば事後分布$p(x | k) = \operatorname{Beta}(x | \hat{a}, \hat{b})$のパラメータは以下のように更新される。

$$\begin{aligned} \hat{a} &= k + ca = 1 + 1000 \times 0.03 = 31 \\ \hat{b} &= n - k + cb = 100 - 1 + 1000 \times 0.97 = 1069 \end{aligned}$$

このとき事後分布の期待値は

$$\begin{aligned} \frac{\hat{a}}{\hat{a} + \hat{b}} &= \frac{k + ca}{(k + ca) + (n - k + cb)} \\ &= \frac{k + ca}{n + ca + cb} \\ &= \frac{1 + 1000 \times 0.03}{100 + 1000 \times 0.03 + 1000 \times 0.97} \\ &\fallingdotseq 0.028 \end{aligned}$$

となるので「100 回引いて 1 回しか当たらないなら本当は確率 2.8% くらいなんじゃない……？」という感じになるが、分布を描画してみると 3% の部分にも十分被っているし、ありえないこともないかということになる。

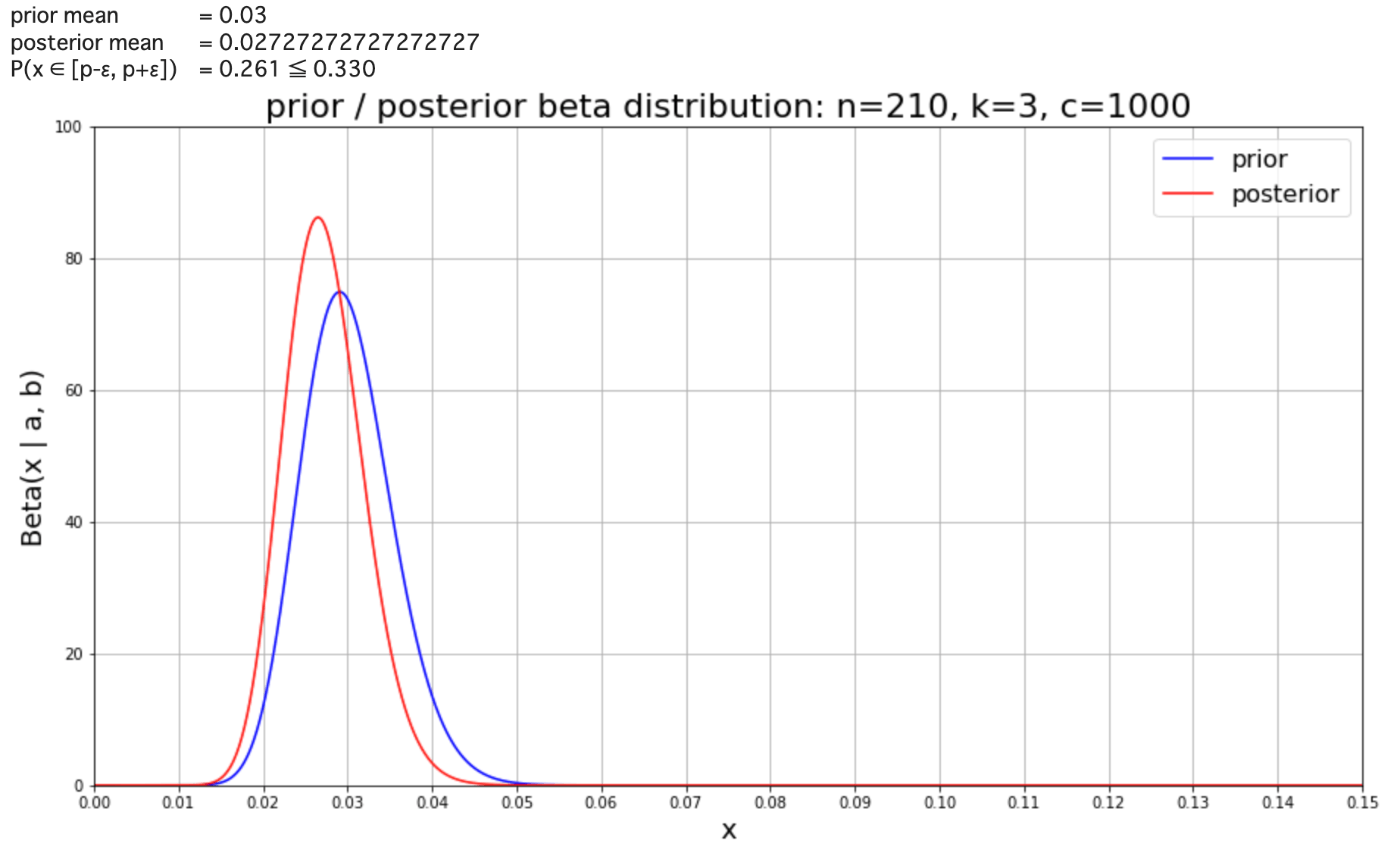
この分布が表示されているアタリ確率$p$に被らなくなるくらいに収束したらおそらく不正が行われている可能性が高く、具体的には

$$P(x \in [p-\varepsilon, p+\varepsilon]) = \int _ {p - \varepsilon} ^ {p + \varepsilon} \operatorname{Beta}(x | \hat{a}, \hat{b}) dx$$

によって「実際のアタリ確率が $p \pm \varepsilon$ の区間に入る確率$P$」を求めることができる。$P(x \in [p-\varepsilon, p+\varepsilon])$が小さくなるケースとしては

• 観測回数が不十分で分布の裾野が広いため $0.03 \pm \varepsilon$ の区間に入る確証はない
• 観測回数が十分で分布の裾野が狭く確実に $0.03 \pm \varepsilon$ の区間には入らないといえる

の 2 パターンがあり、観測回数が増えるに連れて前者から後者へ変化していくが、その「おかしさ」の度合いは

$$P(x \in [\hat{p}-\varepsilon, \hat{p}+\varepsilon]) = \int _ {\hat{p} - \varepsilon} ^ {\hat{p} + \varepsilon} \operatorname{Beta}(x | \hat{a}, \hat{b}) dx$$

と$P(x \in [p-\varepsilon, p+\varepsilon])$を比較することで評価できる。ここで$\hat{p}$は推定されたアタリ確率で

$$\hat{p} = \frac{\hat{a}}{\hat{a} + \hat{b}}$$

である。おおよそ

$$P(x \in [p-\varepsilon, p+\varepsilon]) \leq P(x \in [\hat{p}-\varepsilon, \hat{p}+\varepsilon])$$

が成り立ち（ベータ分布が$\hat{p}$を軸に見たとき対称ではないので$P(x \in [p-\varepsilon, p+\varepsilon]) > P(x \in [\hat{p}-\varepsilon, \hat{p}+\varepsilon])$となることもありうる）、等号成立は$p = \hat{p}$のとき、つまり推定されたアタリ確率が表示されているアタリ確率と完璧に等しいときである。この 2 つの確率の乖離が大きいほど真のアタリ確率は$\hat{p}$に近いと言える。

ちなみに私の条件（$n=210, k=3, c=1000$）だと以下のような感じになる。

import numpy as np
from matplotlib import pyplot as plt
from scipy.stats import beta

# 事前ベータ分布のパラメータ
a = 0.03
b = 0.97

# 事前ベータ分布の分散の調整
c = 1000

# ガチャのアタリ確率（こうなるよう a, b を決める）
p = a / (a + b)

# 何回ガチャを引いたか
n = 210

# 何回アタリが出たか
k = 3

# 事後ベータ分布のパラメータ
a_hat = k + c * a
b_hat = n - k + c * b

# p ± ε の範囲に実効確率が入る確率
p_hat = a_hat / (a_hat + b_hat)
eps = 0.002
P = beta.cdf(p+eps, a_hat, b_hat) - beta.cdf(p-eps, a_hat, b_hat)
P_hat = beta.cdf(p_hat+eps, a_hat, b_hat) - beta.cdf(p_hat-eps, a_hat, b_hat)

# 事前・事後でそれぞれ平均を出力（アタリの確率はこれくらい、という推定）
print(f'prior mean \t\t= {c * a / (c * a + c * b)}')
print(f'posterior mean \t= {a_hat / (a_hat + b_hat)}')

# p ± ε の範囲に実効確率が入る確率
print(f'P(x ∈ [p-ε, p+ε])\t= {P:.3f} ≦ {P_hat:.3f}')

# 確率変数
xs = np.linspace(0, 0.2, 10000)

# 図のサイズ
plt.figure(figsize=(15, 8))

# 事前分布の描画
plt.plot(xs, beta.pdf(xs, c*a, c*b), color='b', label=f'prior')

# 事後分布の描画
plt.plot(xs, beta.pdf(xs, a_hat, b_hat), color='r', label=f'posterior')

# 適当に表示範囲を指定
plt.xticks(np.arange(0, 1, 0.01))
plt.xlim([0, 0.15])
plt.ylim([0, 100])

# その他、図の描画設定
plt.grid()
plt.legend(fontsize=16)
plt.title(f'prior / posterior beta distribution: n={n}, k={k}, c={c}', fontsize=22)
plt.xlabel('x', fontsize=18)
plt.ylabel('Beta(x | a, b)', fontsize=18)
plt.show()

邪悪なガチャを作って遊ぼう

次に気になるのは「バレないように人が課金したくなるような邪悪なガチャを作れるのか？」という部分である。いわゆる「確率調整」というやつをどれだけ簡単にできるか検証してみる。

前提を整理しておこう。まず、ソシャゲのユーザーは

1. 廃課金勢：お金が余ってしょうがない人たち
2. 重課金勢：毎月のようにガチャを天井まで回す
3. 微課金勢：欲しいときだけ、お得なアイテムだけ少額課金
4. 無課金勢：まったく課金しない

の 4 種類に大別される^[4]。それぞれがどれくらいの割合で存在するのかは知らないが、

1. 廃課金勢：いいコンテンツを作り、裾野を広げるとたまに現れる神様
2. 重課金勢：メイン収益源
3. 微課金勢：サブ収益源
4. 無課金勢：裾野を広げてもらうための宣伝役

であり、廃課金勢と重課金勢をメインターゲットとしつつ万人ウケする要素も盛り込んだコンテンツを作成していくのが基本的な戦略になるだろう。

それぞれの層に対してどういった戦術でアプローチするかはコンテンツによりまちまちだと思うが、ガチャの確率調整がもっとも効くのは微課金勢である。廃課金勢、重課金勢は試行回数を稼げるので下手に小細工をするとバレてしまうが、微課金勢や無課金勢は確率表記を多少疑問に思っても検証に必要な試行回数を確保できないし、上手い確率調整で微課金勢がメイン収益源の重課金勢にシフトしてくれれば戦術的勝利と言える。

人がどういったときに思わず課金したくなるかは、よく知られている性質としては

• 欲しいもののために一度課金すると、手に入るまで課金したくなる（引っ込みがつかなくなる）

というものがある^[5]。最近のガチャは天井が存在するので、企業側の戦術としては天井までのアタリ確率を下げればよい。この方法なら微課金勢だけでなく重課金勢からもお金を巻き上げられるので一石二鳥である。

こんな感じのイメージを念頭に、企業（先手）とユーザー（後手）の攻防を考えていく。今後、ゲームに表示されている確率は表示確率、実際に設定されている確率は実効確率と呼ぶことにする。

先手（企業）: 単に表示確率よりも実効確率を下げる

単に表示確率よりも低い実効確率を設定すれば、全てのユーザーはフラストレーションを溜めて課金するに違いない。

後手（ユーザー）: 繰り返しガチャを引き検証する

実効確率が表示確率よりも小さい場合は試行回数を増やすことで不正を検知できる。具体的には本記事の前半で紹介した内容、特にベイズ推定でおおよそ検知することができる。たとえば表示確率が 3% なのに 1000 回中 20 回しかアタリがでなければ、以下のようにかなり怪しいグラフになってくる。また、$P(x \in [p-\varepsilon, p+\varepsilon])$が 16% なのに対して$P(x \in [\hat{p}-\varepsilon, \hat{p}+\varepsilon])$が 43% となっており、$\hat{p}$のほうが信用できる可能性が 2.5 倍も高い。

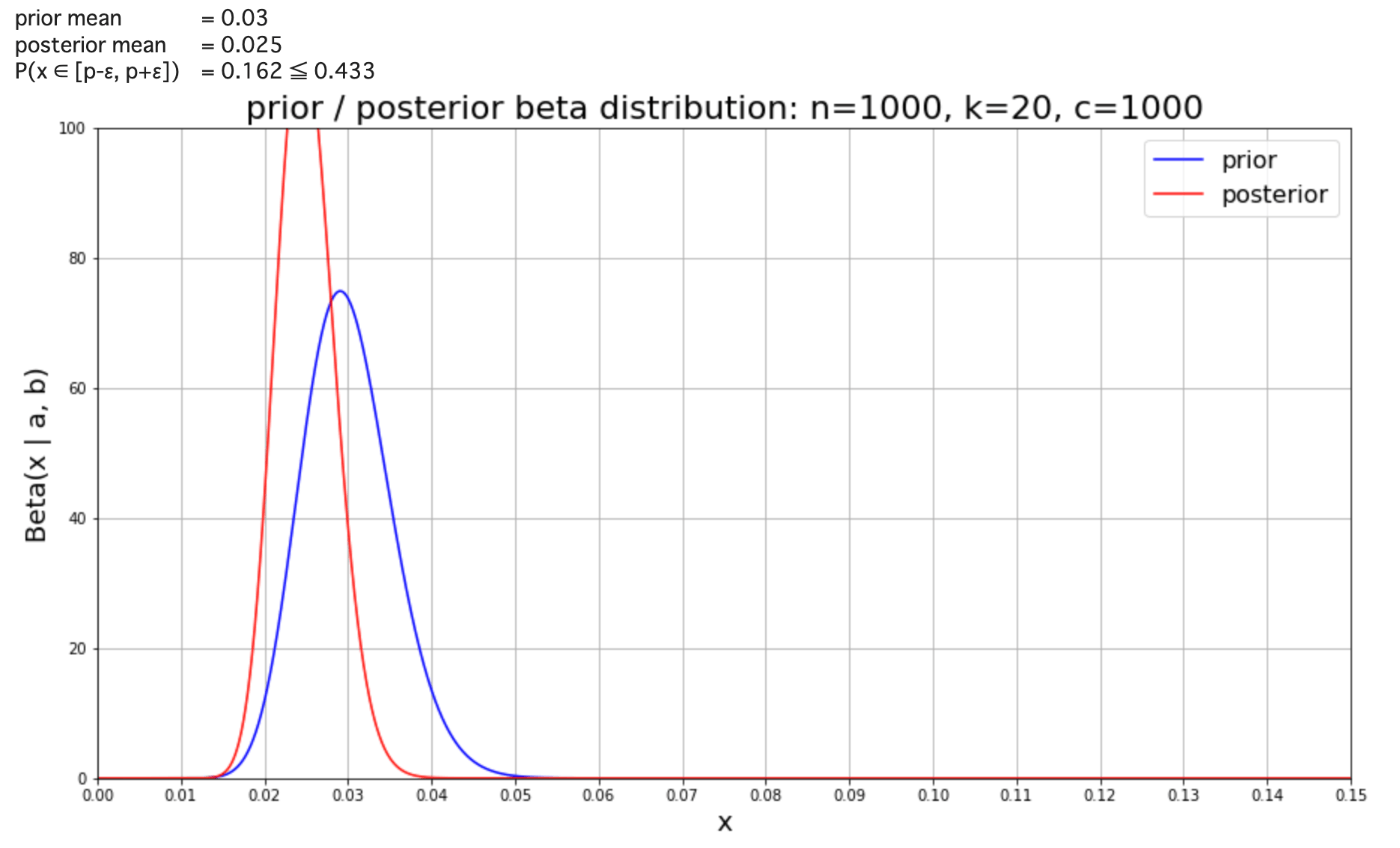
先手（企業）: 天井まで実効確率を下げ、その後少しの間は上げる

大抵の統計的な検証手法はモデルに独立同分布（i.i.d.）を仮定する。独立同分布とは簡単に言えば「何度引いてもガチャが排出される確率は毎回同じ」ということで、逆にこの前提を崩すような確率の設定をすれば大抵の統計的手法はワークしなくなる。

裁判沙汰になっている例では「アタリが出るまで引いてみた」系の動画が発端になっていたりするから、まず「同じ人がガチャを引き続ける」というケースを想定し、「天井まで実効確率を下げ、その後少しの間は上げる」という方法で繰り返し引いたときに表示確率に収束にするように調整する。

ウマ娘のサポートカードガチャの天井は 200 回、完凸（4凸）まで 1000 回だから、これを参考にシステムを組む。企業としては2凸分（61200円）課金させられれば成功と考えて、実効確率を2凸までは$\rho$だけ下げ、そこから4凸までとその後の 200 回は$\rho$だけ上げておき、その後表示確率に戻すものとする。このような邪悪なガチャをエミュレートすると以下のようになる。

以下の図では$\rho = 0.005$なので、赤線の部分でアタリ確率を大胆にも 0.5% も動かしている。そのせいで 600 回目までは露骨にアタリが少ないが 1200 回目までの間にこっそり増えるので、1000回目、5000回目で統計を取っても本記事で作成したベイズ推定による不正検知では検知できない。

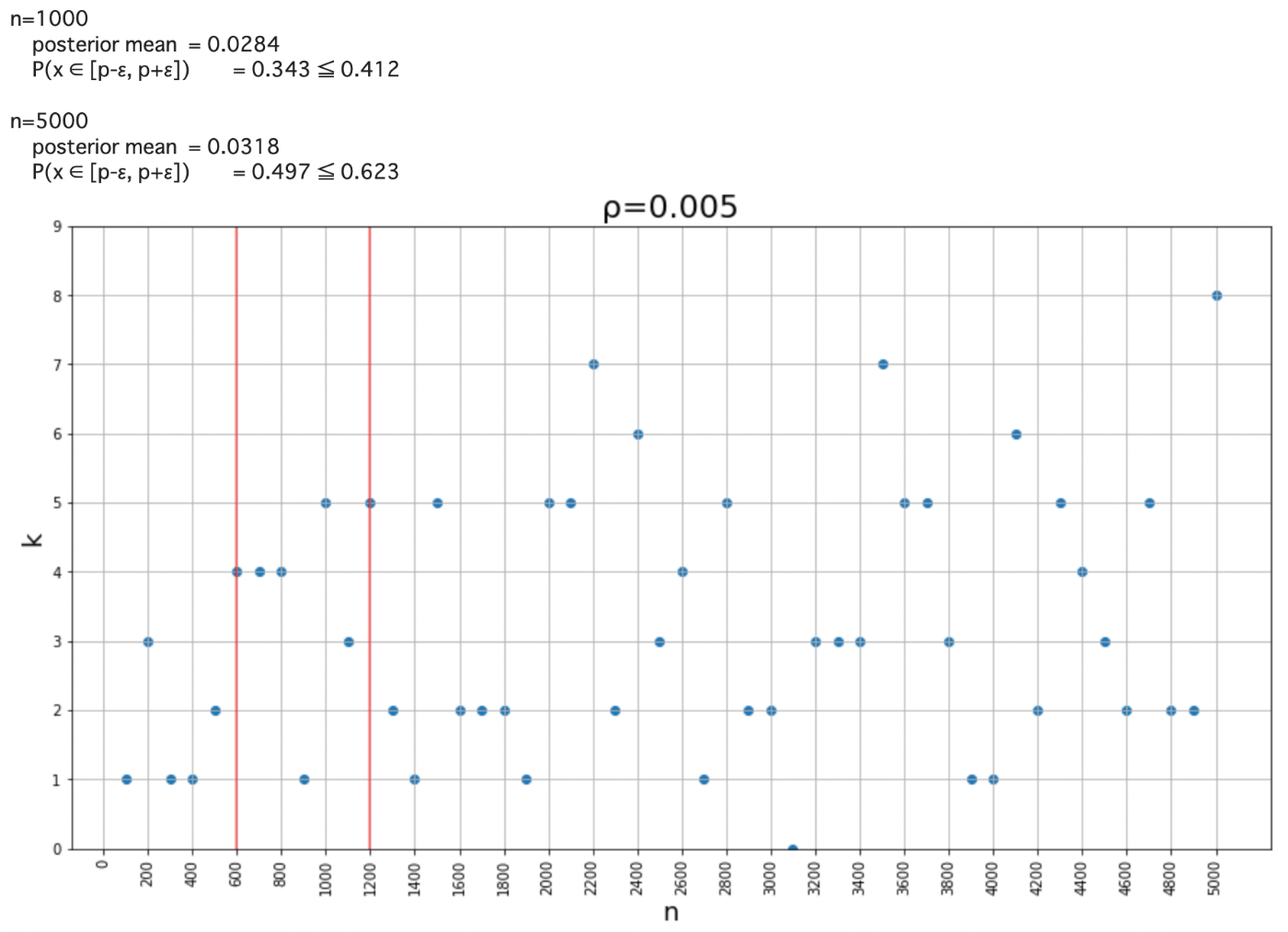
検証に用いたコード

# 天井まで実効確率を下げ、その後少しの間は上げる という邪悪なガチャをエミュレート
np.random.seed(43)

# 事前ベータ分布のパラメータ
a = 0.03
b = 0.97

# 事前ベータ分布の分散の調整
c = 1000

# ガチャのアタリ確率（こうなるよう a, b を決める）
p = a / (a + b)

# 確率調整
rho = 0.005

ks = []

for i in range(6):
  ks.append(binom.rvs(100, 0.03-rho))
for i in range(6):
  ks.append(binom.rvs(100, 0.03+rho))
for i in range(38):
  ks.append(binom.rvs(100, 0.03))

ks = np.array(ks)
xs = np.arange(100, 5000+1, 100)

# 事後ベータ分布のパラメータ
k_1000 = ks[:10].sum()
k_5000 = ks.sum()

a_hat_1000 = k_1000 + c * a
b_hat_1000 = 1000 - k_1000 + c * b

a_hat_5000 = k_5000 + c * a
b_hat_5000 = 5000 - k_5000 + c * b

# p ± ε の範囲に実効確率が入る確率
p_hat_1000 = a_hat_1000 / (a_hat_1000 + b_hat_1000)
p_hat_5000 = a_hat_5000 / (a_hat_5000 + b_hat_5000)
eps = 0.002

P_1000 = beta.cdf(p+eps, a_hat_1000, b_hat_1000) - beta.cdf(p-eps, a_hat_1000, b_hat_1000)
P_hat_1000 = beta.cdf(p_hat_1000+eps, a_hat_1000, b_hat_1000) - beta.cdf(p_hat_1000-eps, a_hat_1000, b_hat_1000)

P_5000 = beta.cdf(p+eps, a_hat_5000, b_hat_5000) - beta.cdf(p-eps, a_hat_5000, b_hat_5000)
P_hat_5000 = beta.cdf(p_hat_5000+eps, a_hat_5000, b_hat_5000) - beta.cdf(p_hat_5000-eps, a_hat_5000, b_hat_5000)


# 事前・事後でそれぞれ平均を出力（アタリの確率はこれくらい、という推定）
print('n=1000')
print(f'    posterior mean \t= {(k_1000 + c * a) / (1000 + a + c * b) :.4f}')
print(f'    P(x ∈ [p-ε, p+ε])\t= {P_1000:.3f} ≦ {P_hat_1000:.3f}')
print()
print('n=5000')
print(f'    posterior mean \t= {(k_5000 + c * a) / (5000 + c * a + c * b) :.4f}')
print(f'    P(x ∈ [p-ε, p+ε])\t= {P_5000:.3f} ≦ {P_hat_5000:.3f}')

plt.figure(figsize=(15, 8))
plt.vlines([600, 1200], 0, 10, color='r', alpha=0.6)

plt.scatter(xs, ks)

plt.xticks([0] + list(xs[1::2]), rotation=90)
plt.grid(True)
plt.title(f'ρ={rho}', fontsize=22)
plt.xlabel('n', fontsize=18)
plt.ylabel('k', fontsize=18)
plt.ylim([0, 9])
plt.show()

後手（ユーザー）: 20人で結託してそれぞれ500連ガチャ

ガチャを何回引いたかによって確率調整を入れるアルゴリズムは、ひとりのユーザーで検証することは困難である（試行回数を重ねるほど表示確率に収束するから）。対抗手段としては

1. 異なる時期に実施されたガチャのそれぞれについて最初の 500 連を記録して統計を取る
2. 異なるユーザーがそれぞれ最初の 500 連を記録して統計を取る

といった方法で不正を検知できる可能性があるが、ひとりで検証するのに比べて格段に検知は難しくなる。

先手（企業）: 15人にひとりの割合でカモを選ぶ

さらに上記のユーザーによる不正検知をすり抜ける方法として「15人にひとりくらいの割合でカモを選ぶ」という方法がある。つまり

1. 確率操作を行う相手は 15 人にひとりくらいの割合でランダムに選ぶ
2. 確率操作を行う相手はガチャごとに変える

までやられた場合、ユーザーによる検知はほぼ不可能になる。仮に100人が検証に参加したとして、その中に 10 人くらい「運が悪いやつ」がいても、確率操作なのかたまたま本当に運が悪いやつが多かっただけなのか区別できないのである。同じ人が繰り返しガチャを引いてその事実を確かめることはできない（既にその検証方法は対策されている）から、この不正を検知するには検証に参加するユーザーの人数を増やすしかない。しかしそれは実際には難しいからユーザーが現実的なコストでこの不正を検知する手段はない。以上、5手をもって企業の勝利である。

おしまい

コロナでホテル療養中だから暇だったんだよ。かなり気をつけて対策しててもかかるくらい運が悪かったわけだからガチャの出が悪いくらいじゃ驚かないね。頸椎ヘルニアもやらかすし今年は厄年か？

脚注

1. ゲームはポケモンの個体値厳選を無限にやる感じです。好き嫌い分かれると思いますね。

2. 特に期待値$np > 5$かつ分散$np(1-p) > 5$のとき。

3. 小さくしすぎると$x = 1$のほうもありえる、という感じの分布になってしまうので$10$未満はおすすめしない。

4. 私は楽しんだゲームには楽しんだ期間だけサブスク料という形で課金するタイプである。私がゲーム制作者だったら「散々遊んだくせに金を払わない連中とか呪い殺したい」と思うだろうからである。まったく関係ない話だが、けっこうな量の記事を投稿している Zenn での私の現在までの収益は 0 円である。

5. 一般に、人間は一度犠牲を払ってしまうとその犠牲を無駄にしたくないという心理が働いて、目的が達成されるまでさらなる犠牲を払う傾向にある。この感情を制御できない人はガチャ、ギャンブル、株、FX、思わせぶりな異性などに手を出してはいけない。