One-Hot 表現を SVM に突っ込むとどうなる？

実験の部分が書きかけです。時間があるときにアップデート予定です。

はじめに

正確には入力される説明変数に実数と One-Hot 表現が混在しているデータを、内部でカーネル関数を用いるアルゴリズムに入力するとどうなるのかという疑問です。そんなことをして OK なのか NG なのか。

職場で質問があって直感的に NG と言ったのですが「なんで」「具体的に」と言われてパッと答えられず、申し訳ない思いをしたので、One-Hot 表現がモデルに影響を与えるケースについていろいろ考察してみました。

結論から言えば、直感に反して、前処理としてスケーリングさえかけていれば SVM にそのまま突っ込んでも OK でした。

直感的に NG ？

内部でカーネル関数を用いるアルゴリズムとは、カーネル法やガウス過程に基づく手法のことです。非線形 SVM は線形 SVM をカーネル法で拡張したものなのでこれに該当します。

カーネル関数$k(x, x ^ \prime)$はイメージ的にはデータ点$x$と$x ^ \prime$の入力空間での「近さ」や「類似度」を測る関数です。

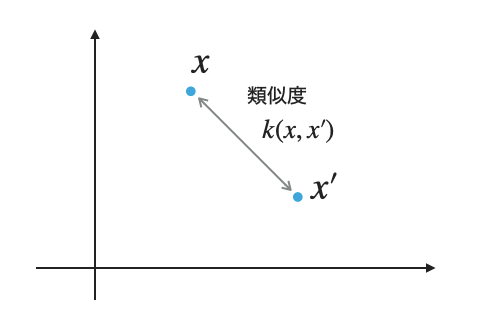
カーネル関数は対称性と（半）正定値性さえ満たせば自由なものを選ぶことができます。これは逆に言えば、適切にデータの「近さ」を測れるように入力空間とそれに対応するカーネル関数を自分で設計しなければならないということでもあります。

scikit-learn の SVC や SVR はデフォルトで RBF カーネル、つまりガウスカーネルを用いています。ガウスカーネルの定義は

$$k(x ^ {(i)}, x ^ {(j)}) = \exp( - \beta \| x ^ {(i)} - x ^ {(j)} \| ^ 2)$$

です（ただし$\beta$は正の定数）。ここで$\| \cdot \|$はベクトルの Euclid ノルムなので、ガウスカーネルは暗黙に入力空間が Euclid 空間であることを期待していると考えられます。もちろん入力される変数の組の各要素が実数に属していればガウスカーネルは定義できてしまいますが、ガウスカーネルはそれを無理やり Euclid 距離の構造で測ってしまうということです。

ここで生じる疑問として、ガウスカーネルはベクトルの一部に One-Hot 表現が含まれているときにうまくデータ間の「近さ」を測ってくれるのでしょうか？

これは他の職業の人はともかくとして、データサイエンティストを名乗る人間だけは「本当にそんなことしていいの？」と一度は問うべき問題です。

したがって「やっていいの？」と聞かれたら私は立場上、黄色信号を出さざるを得ないのです。

One-Hot 表現とは

$n$種類の状態が存在するデータを表現するとき、変数の組$(x _ 1, x _ 2, \ldots, x _ n)$を用いて、$k$番目（$1 \leq k \leq n$）の状態に対して、$k$番目の変数だけが$1$でそれ以外が$0$、すなわち、

$$x _ i = \begin{cases} 1 & \text{if} \,\, i = k \\ 0 & \text{otherwise} \end{cases}$$

とするような表現方法を One-Hot 表現といいます。

One-Hot 表現は有限個の状態に対して適当な値を割り振るのが難しいときによく用いられます。たとえば性別は$\{ \text{m}, \text{f} \, \}$の二種類（有限個）の状態を取り、これを回帰や分類のアルゴリズムに入力するときはなんらかの数値に直す必要がありますが、$\text{m}$と$\text{f }$にそれぞれどんな数値を割り振ったらよいかは自明ではありません。そこで

$$\begin{cases} \text{m} &= (1,0) \\ \text{ f} &= (0,1) \end{cases}$$

とするのが One-Hot 表現です。昨今の事情に配慮して「その他（$\text{o}$）」という性別が追加されたときにも

$$\begin{cases} \text{m} &= (1,0,0) \\ \text{ f} &= (0,1,0) \\ \text{ o} &= (0,0,1) \end{cases}$$

とすることで対応できます。多くのケースで、上記の各式の$1$に任意の実数（それぞれ異なってもよい）をかけた表現も本質的には同じ表現になります^[1]。

他のあまりよくない表現

他にも簡単に思いつくのは

$$\begin{cases} \text{m} &= 0 \\ \text{ f} &= 1 \end{cases} \qquad \begin{cases} \text{m} &= -1 \\ \text{ f} &= 1 \end{cases}$$

の二種類です（こちらも定数倍は無意味です）。

ここに「その他（$\text{o}$）」という性別が追加されたときに、$\{0, 1\}$や$\{-1, 1\}$の表現を採用していると、どんな数値を割り振ればよいかわからなくなります。本当にそんなことをしていいかはさておき、苦し紛れに

$$\begin{cases} \text{m} &= 1 \\ \text{ f} &= 2 \\ \text{ o} &= 3 \end{cases} \qquad \begin{cases} \text{m} &= -1 \\ \text{ f} &= 1 \\ \text{ o} &= 0 \end{cases}$$

などとすることはできます。

これらの表現はどれもあまりよくない表現です。正負の符号は「反対方向」の構造を、1,2,3 といった数値は「順序」や「距離」の構造をデータに強制してしまうからです。また、$0$ は特別な数字で、どんな数値をかけ算しても $0$ にしてしまう（重み付けを無効化する）という特殊な性質をデータに与えてしまいます。

One-Hot 表現は「方向」の構造くらいしか持たないので、データに対する仮定が少ない表現と言えます。

実数/ One-Hot 混在表現

これは実際のデータ解析でよく発生するのですが、説明変数の組$(x _ 1, x _ 2, \ldots, x _ n)$のうち、一部が One-Hot 表現に対応していて、残りの変数が実数データになっていることがよくあります。たとえば性別に身長、体重などのデータが追加されているケースです^[2]。

$\mathbb{R} ^ n$を$n$次元の Euclid 空間、$\mathbb{I} _ m$を$m$種類の状態を表現できる One-Hot 表現の空間とします。この記事で今後使っていくデータ表現は、この状況のもっともシンプルなケース、$n = 1, m = 2$の$\mathbb{R} \times \mathbb{I} _ 2$とします。つまり、各データは

$$\begin{aligned} x ^ {(1)} &= (1.42, 1, 0) \\ x ^ {(2)} &= (9.66, 0, 1) \\ \end{aligned}$$

のような形式を取ります。

実数/ One-Hot 混在表現（長いので今後は混在表現と呼ぶことにします）は、解釈としては One-Hot 表現により区別される実験系の入力データに対応します。

線形回帰と混在表現

混在表現を線形回帰に入力すると定数項（切片）の切り替えを意味します。混在表現の入力$x \in \mathbb{R} \times \mathbb{I} _ 2$と出力$y \in \mathbb{R}$についての線形回帰の式は

$$y = w ^ \mathrm{T} x = (\, m \,\,\, b \,\,\, c \,) \left( \begin{matrix} x _ 1 \\ x _ 2 \\ x _ 3 \end{matrix} \right) = m x _ 1 + b x _ 2 + c x _ 3$$

です。$x _ 2, x _ 3$はどちらか一方が$1$でもう片方が$0$なので、この式は

$$\begin{cases} y &= m x _ 1 + b \\ y &= m x _ 1 + c \end{cases}$$

という二つの平行な直線の方程式に相当します。一般化すれば、One-Hot 表現で区別される複数の実験系において出力が完全に定数シフトの関係にあるときだけ、混在表現による線形回帰はうまくいくことになります（説明変数に任意の特徴量$\phi(x _ 1)$を加えることができるので、たとえば多項式回帰など直線や平面より複雑な出力にも対応できますが、One-Hot 表現の部分は定数シフトになります）。

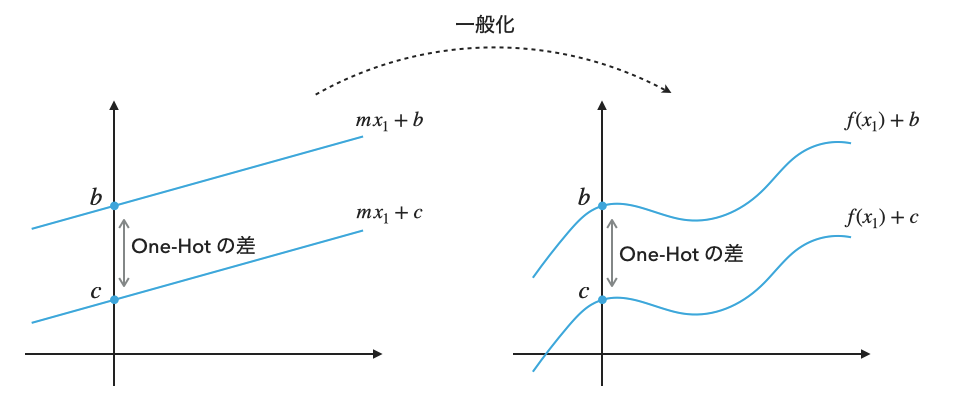
線形回帰と他のあまりよくない表現

先ほど紹介した「他のあまりよくない表現」は、One-Hot 表現の代わりに状態に適当な数値を割り振る表現でした。状態に適当な数値を割り振った集合を$\mathbb{X}$とおけば、これと実数の混在表現は$(x _ 1, x _ 2) \in \mathbb{R} \times \mathbb{X}$で表されます。同様に線形回帰の式を立てれば

$$y = m x _ 1 + c x _ 2$$

です。つまり人為的に決めた状態の値で定数項（切片）が決まってしまうモデルとなり、$y$に対する当てはまりが非常に悪くなるでしょう。

決定木と混在表現

RandomForest などの決定木系のモデルは、何も考えずに混在表現を入力したとしても、おそらくあまり問題がありません。もともと説明変数に対して条件分岐を繰り返すモデルなので、One-Hot の部分に対して $0$ か $1$ かで条件分岐を行うことは、実数の部分に対してある値$a$よりも大きいか小さいかで条件分岐を行うことと大差がないからです（たとえば実際に$0.5$よりも大きいか小さいかで $0$ か $1$ かを判別することができます）。

なんなら「他のあまりよくない表現」で紹介した表現でも、木の深さとデータ数が十分なら特に問題なく学習してくれそうな感じがします。

線形回帰や SVM と違って理論的に評価するのが難しいので実験してみないとわからないですね。

SVM と混在表現

カーネル法で拡張された SVM は「入力空間で近くにあるデータは出力も近い値を取るはず」という、k-近傍法に近い考え方をモデル化したものになっています。

いまは何も考えずにガウスカーネルを使った場合に着目して議論しているので、ガウスカーネルについて式変形してみましょう。

$$\begin{aligned} k(x ^ {(i)}, x ^ {(j)}) &= \exp( - \beta \| x ^ {(i)} - x ^ {(j)} \| ^ 2) \\ &= \exp\Bigl( - \beta \bigl\{ (x _ 1 ^ {(i)} - x _ 1 ^ {(j)}) ^ 2 + (x _ 2 ^ {(i)} - x _ 2 ^ {(j)}) ^ 2 + (x _ 3 ^ {(i)} - x _ 3 ^ {(j)}) ^ 2 \bigr\} \Bigr) \end{aligned}$$

One-Hot 表現の部分がデータ間の距離に与える影響は、$x ^ {(i)}, x ^ {(j)}$の One-Hot 表現の部分のうちそれぞれ$k, \ell$番目が$1$だとすれば

$$(x _ 2 ^ {(i)} - x _ 2 ^ {(j)}) ^ 2 + (x _ 3 ^ {(i)} - x _ 3 ^ {(j)}) ^ 2 = \begin{cases} 0 & \text{if} \,\, k = \ell \\ 2 & \text{otherwise} \end{cases}$$

です。

One-Hot 表現は異なる実験系の切り替えを意味していたことを思い出せば、これは$x _ 1$が等しい異なる実験系の点を必ず$2$の距離に置いていることを意味します。つまり

• 同じ実験系で$(x _ 1 ^ {(i)} - x _ 1 ^ {(j)}) ^ 2 = 2$となるデータ
• 異なる実験系の$x _ 1$が等しいデータ

の二つをまったく同じ重要度で評価することを暗黙に仮定してしまいます。異なる実験系でのデータが、必ずしももう一方の実験系でのデータを説明するために役に立たないケースは問題を発生させるかもしれません。

しかしこの仮定は、

1. 前処理としてスケーリングを行なっている
2. 実数変数の個数が十分に少ない（$\mathbb{R} \times \mathbb{I}_m$とか$\mathbb{R} ^ 2 \times \mathbb{I}_m$）

という条件が満たされる限り、ほとんど問題になりません。メカニズムとしては、スケーリングによってほとんどの場合、同じ実験系の点が異なる実験系の点よりも近くにくるからです。

スケーリングは各変数からその平均を引き、標準偏差で割ったものです。One-Hot 表現は値が$\{0,1\}$で固定なので、$0$ と $1$ がそれぞれいくつあるかの割合で決まる標準偏差が大きいほど二つの実験系が「近く」なります。標準偏差は $0$ と $1$ が同数のときに最大となり、その値は約$0.5$です^[3]。したがってスケーリング後は二つの実験系がもっとも近くなるときでも

$$(x _ 2 ^ {(i)} - x _ 2 ^ {(j)}) ^ 2 + (x _ 3 ^ {(i)} - x _ 3 ^ {(j)}) ^ 2 = \begin{cases} 0 & \text{if} \,\, k = \ell \\ 8 & \text{otherwise} \end{cases}$$

となり、距離$8$の位置にあります。

一方で実数変数については、あるデータ点から$1 \sigma$離れた点がスケーリングによって距離$1$とみなされ、異なる実験系の点は最低でも$\sqrt{8}\sigma = 2.8\sigma$の位置にあります。分布の仕方にもよりますが、仮にガウス分布していたと仮定すると、$2.8\sigma$は十分遠い位置に当たり、同じ実験系の点がそれ以内に十分に含まれうると言えます。

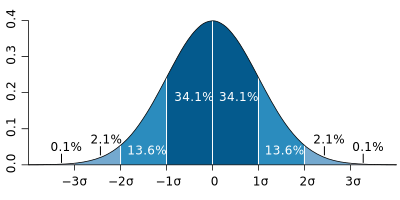
M. W. Toews - 投稿者自身による作品, based (in concept) on figure by Jeremy Kemp, on 2005-02-09, CC 表示 2.5, https://commons.wikimedia.org/w/index.php?curid=1903871による

$\mathbb{R} ^ n \times \mathbb{I} _ m$の$n$が大きいと、個々の変数の距離の累積和が距離$2.8$を容易に超える可能性があります。そうなると異なる実験系のデータが予測に混ざり込んでくる可能性があります。

まとめると、

• 前処理としてスケーリングを行わなかったとき
• $\mathbb{R} ^ n \times \mathbb{I} _ m$の$n$が大きいとき

の少なくとも一方を満たすときは気をつける必要があります。

---

ここから先執筆中です。

実験

混在表現はまったく異なる実験系を同じデータシートにまとめてしまうことができるので、たとえば以下の図のようなケースも当然あり得ます。

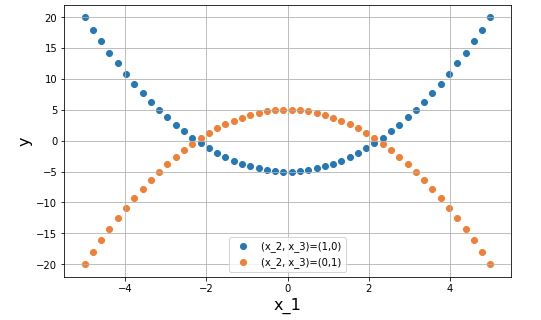
青、橙の曲線はいずれも二次関数ですが、$x _ 2, x _ 3$のどちらが$1$であるかによって符号が反転しています。これはたとえば$x _ 2, x _ 3$が「どの電流計で計測したか」の One-Hot 表現だった場合に、電流計を繋ぐ方向によって符号反転が起こるはずなので、実際の問題でも容易に発生しえます。なんならこの擬似データは

$$f(x, z) = x ^ 2 z + (z ^ 3 - 6 z)$$

を用いて、

$$\begin{aligned} x &= x _ 1 \\ z &= x _ 2 - x _ 3 \end{aligned}$$

と変数変換して描画したものですから、実際の現象としては下図のような構造を取っていて、たまたま私たちが$z = 1, -1$の地点で観測していただけ（他の場所にも電流計を設置することが可能）といういかにもありがちなケースです。

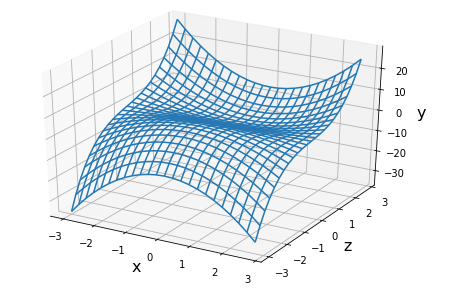
さて、実際のデータはこんなに均等にデータ点を収集できず、以下の図のように歯抜けになっていることがほとんどです。

いま、橙色の$x _ 1 = -1$付近はほとんどデータがないので、この辺りを予測しようとすると青色の$x _ 1 = -1$付近のデータが「入力空間上でもっとも近くにある」ので予測に使われることになり、予測値は下図のように負の方向に大きく引っ張られることになります。

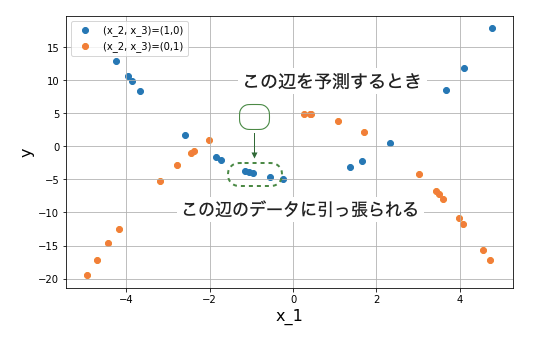
これはおそらく、橙色のデータと青色のデータをそれぞれ別々に SVR で回帰するよりも悪い予測結果になるでしょう。別の実験系のデータが影響を与えないくらい高密度でデータを観測すればこの問題は起こらないかもしれませんが、最初から分けておけば、より少ないデータ数で精度よく近似ができるはずです。

おわりに

実数/ One-Hot 混在表現がモデルに与える影響について考察しました。みなさまのデータ解析に役立てていただければ幸いです。

脚注

1. たとえば線形回帰、決定木、ニューラルネットなどに基づくモデルでは定数倍をモデルが吸収してくれますし、モデルが吸収してくれない場合でも前処理としてスケーリングを行えば定数倍は打ち消されます。

2. 身長と体重はいずれも正の値のみを取るので、厳密に言えばこの場合も$\mathbb{R} _ +$の空間に Euclid 空間的な構造を仮定できるのかという疑問が生じます。実際にやるかどうかはさておき、一応、正の値しか取らないデータは対数を取ることで実数空間$\mathbb{R}$に写せるというテクニックがあります。

3. データ数が奇数個か偶数個かによって若干変わり、データ数が無限大の極限で$0.5$に収束します。