Open3
Pythonで学ぶ音源分離を読むぞ
背景とか動機とか。
- 背景
- 同じシリーズの合成音声が良かったから。
- また、以前dmmの70%offの時に買って積読にしていたのを思い出して(発見して)、読んでみようと思った。(で、本書のリンクを張ろうと思ってアマゾンを調べたら、primeで無料になってるな。むぅ、まぁ、70%offだったからいいか。)
1章
第1節 不要な音の除去
- 不要な音:干渉音、背景雑音、残響音
- 音源分離:不要な音と欲しい音が混ざった音(混合音)から欲しい音(きれいな音)だけ取り出すこと。(思ったより狭い範囲だな。話者分離とかは入らないのか。)

第2節 直感的な理解
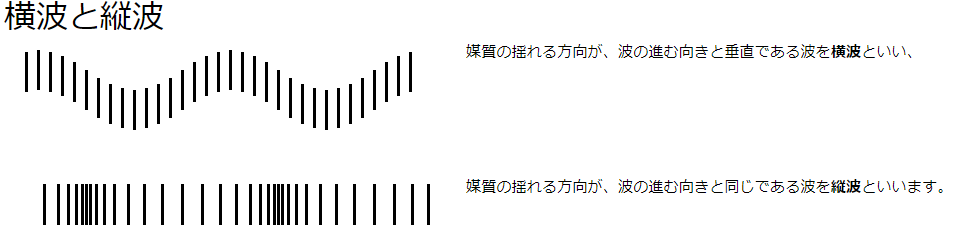
- 波には縦波、横波がある。音は粗密が伝わる縦波。(参考)
- 音の混ざり方は複数の音が足されるだけ。
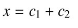
- 音源分離では、空間モデルと音源モデルという二つのモデルを使う。
- 空間モデルは複数のマイクからの入力を使うモデル。音の大小や入力される時間差を使う。a_n_mからs_nの連立方程式を作り解く。

- 話者の位置がわかればa_n_mを推定できるかもしれないが、仮定として強すぎる。(ロボット関連ではカメラから話者の位置を推定するとかできるかも。)
- 音源モデル:ブラインド音源分離。a_n_mをランダムの値としたて連立方程式を解き、s_nが音声っぽければa_n_mが正しい。という考え方。
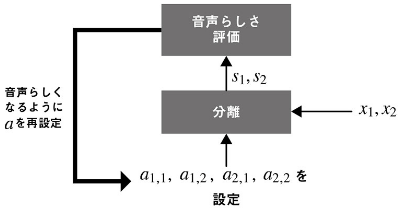
コラム
ふむ。

2章
第2節 周波数領域
-
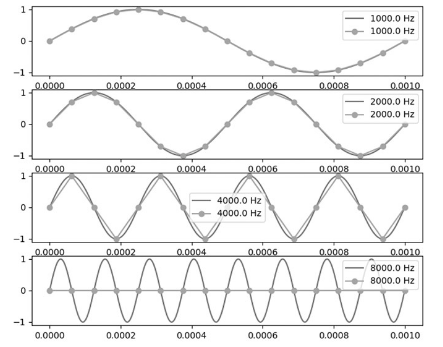
ナイキスト周波数:サンプリング周波数の半分より上の周波数。この周波数はうまく復元できない。(下の図だと12kと4kが同じにみえる。16kと8kも同じ。)
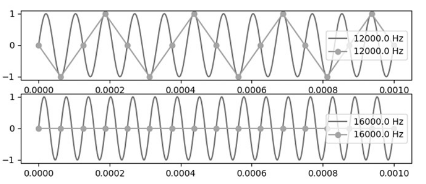
-
ナイキスト周波数を録音しないようにローパスフィルタを通す
-
時間領域から周波数領域に音声データを変換すると時間軸がなくなるので、音声処理では短い区間で区切って、それを時系列に並べる。一つのデータをフレームと呼ぶ。(音声合成の方でも書いてあった)
-
大体数十ミリくらいなら音声の振幅が一定と考えられるので、その単位で短時間フーリエ変換する。フレームはおーばラップさせるとよい。大体1/2や3/4くらい。
-
窓関数:ハニング窓、ハミング窓
-
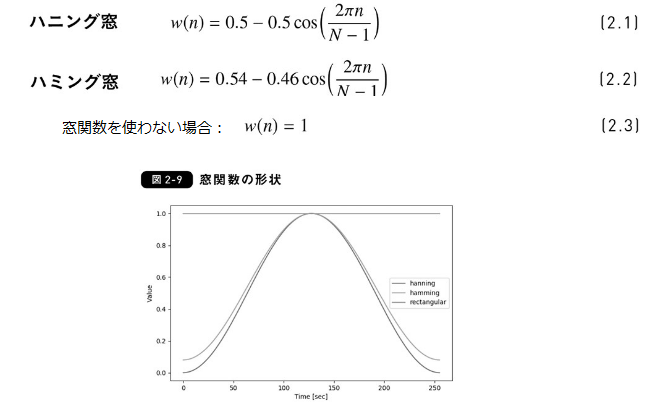
-
フレームℓのn番目の値。L_shiftはフレームごとのシフト。(N - L_shiftがオーバラップの幅になる。)。ℓ * L_sfhitはフレームのオフセット。
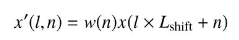
-
この値に短時間フーリエ変換を実行。
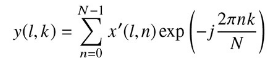
-
いきなりのオイラーの公式(笑&汗)
- 説明の順番を入れ替えたいなぁ。
- 複素数z=x+jyは、|z|=rの時、極形式でz=r(cosΘ+jsinΘ)と書ける。オイラーの公式からexp(jΘ)=cosΘ+jsinΘだから、z=rexp(jΘ)。ということ(?)だと思った。

-オイラーの公式で exp(jΘ) = cosΘ+jsinΘとexp(-jΘ)= cosΘ-jsinΘとする。お互いを足して、2で割ると式2[2.18]。お互いを引いて2で割ると式[2.19]
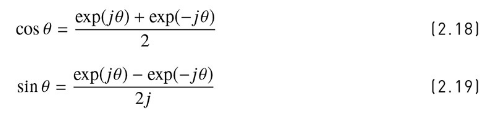
- 式[2.20]わからん。なんで振幅A_lfと位相Θ_lfがわかると式[2.20]になるのだ?cosの波の振幅がA_lfなのはいいけど、なんでcos波?あと、位相の2πfn/F_sってなんぞ?。ああ、2πfn/F_sはオフセットか。
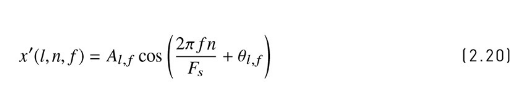
- 式[2.21]は足しただけ。

- 式[2.22]はオイラーの公式を代入しただけ。

- 以降、フーリエ変換の流れ。まぁ、わかったふりをする。
第3節 可視化
- デシベル
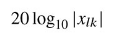
第4節 時間領域領域
- 音源分離では、時間領域の音声波形を、周波数領域の音声波形にして処理を行った後、時間領域の音声波形に戻す。
第5節 周波数領域での音声加工
- スペクトルサブトラクション:雑音のパワースペクトルの平均値を推定し、雑音を含んだ入力信号のパワースペクトルから引くことで雑音の低減を行う方法
- ウィナーフィルタ:原信号と観測信号の定常性を仮定。原信号の最小平均二乗誤差(MinimumMeanSquareError)推定量を得る時不変フィルタ。
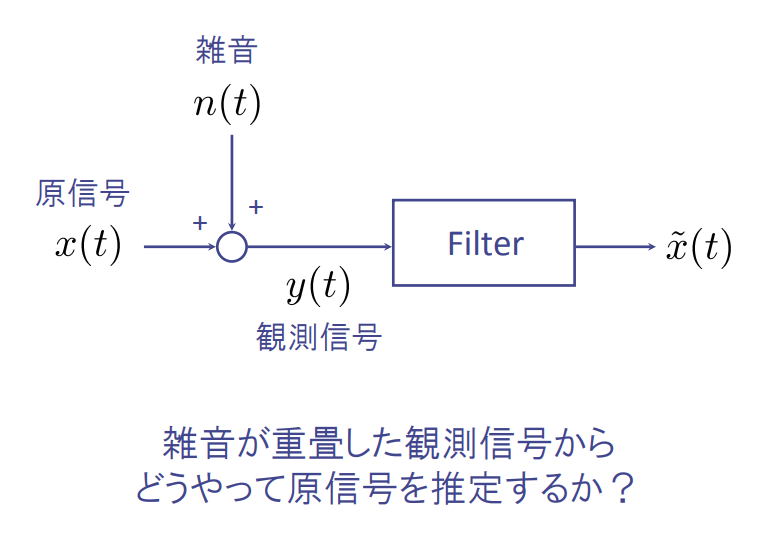

(参考)