前回のおさらい
前半は BM25 の以下について解説しました。
- 対数オッズ比を使ったとしたスコアリング方法である事
- ロバートソン/スパルクジョーンズ重み付け関数 w_t
- Binary Independence Model (BIM)
これにより、前半の冒頭であげた課題のうち、複数単語で検索した時の優先順位付けの問題が解決できるようになりました。現在以下の課題が残っています。
課題3: 出現頻度の考慮
- 「a が 2 回」と「b が 3 回」はどちらの方が関連しているか?
課題4: ドキュメントの長さが色々ある
- 「a の出現数が 2 倍、文章の長さが 4 倍」の場合はより関連していると言えるのか?
その他にもいくつか課題があります。
課題5: キーワードがドキュメントに直接的に現れない
- 「a が主要なテーマだからこそ直接的な明言がされてない」場合がある
課題6: クエリにはない要求がある
出現回数の考慮
まずは課題3について考えてみましょう。 「a が 2 回」と「b が 3 回」はどちらの方が関連しているのでしょうか。
この問題を解決するため、BM25 ではドキュメントの特性を二値のベクトルではなく単語の出現回数のベクトルに拡張します。(F_t および f_t は t の出現回数)
D=(F_1,F_2,…)\\d=(f_1,f_2,…)
w_t(前回の「ロバートソン/スパルクジョーンズ重み付け関数」参照) における t を F_t=f_t に差し替えた関数 w^f(f_t) を導入します。
\LARGE{\begin{align*}
w^f(f_t) &= log(\dfrac
{\color{limegreen} p(F_t=f_t | r)p(F_t=0 | \overline{r})}
{\color{red} p(F_t=f_t | \overline{r})p(F_t=0 | r)}
)
\end{align*}}
Eliteness
p(F_t=f_t | r) は何になるのでしょうか。これを確率的に推測するために、eliteness という概念を持ち込みます。「t をトピックとしたドキュメントである」という事を elite であると呼びます。
「t を含んだドキュメントは t をトピックとしている」、つまり f_t > 0 であれば elite である言えるでしょうか? 例えば10ページの文章の中に一度しか t が出現しない場合、おそらく elite ではないでしょう。t をより多く含む場合、例えば f_t > 10 の場合はどうでしょう? おそらく elite である可能性が高くなるでしょう。しかしそれでも確実に elite であるとは言い難いです。
「ランダムで取り出したドキュメントが elite である」事象を e として、p(F_t=f_t | r) を『「r」 → 「e」 → 「F_t=f_t」』と『「r」 → 「\overline{e}」 → 「F_t=f_t」 』の2ケースに分解します。
p(F_t=f_t | r)
= p(F_t=f_t | e,r)p(e|r)
+ p(F_t=f_t | \overline{e},r)p(\overline{e}|r)
同様に p(F_t=f_t | \overline{r}) に対しても変形し、これらの式を元に w^f(f_t) を計算してみます。
\large{w^f(f_t) = }
log(
\scriptsize{
\dfrac{
(
p(F_t=f_t|e,r)p(e|r)+
p(F_t=f_t|\overline{e},r)p(\overline{e}|r)
)
(
p(F_t=0|e,\overline{r})p(e|\overline{r})+
p(F_t=0|\overline{e},\overline{r})p(\overline{e}|\overline{r})
)
}{
(
p(F_t=f_t|e,\overline{r})p(e|\overline{r})+
p(F_t=f_t|\overline{e},\overline{r})p(\overline{e}|\overline{r})
)
(
p(F_t=0|e,r)p(e|r)+
p(F_t=0|\overline{e},r)p(\overline{e}|r)
)
}
})
となります。
2ポアソンモデル
さて、目が潰れそうな式が爆誕しましたが、ここでポアソン分布 g(x, \mu) を使った仮定を追加します。
ポアソン分布とは?
Wikipedia にあるような確率のグラフを描く分布の事を言います。
ポアソン分布は、一定の期間や条件でランダムな事象がx回起こる確率などに現れる分布です。例えば「1分辺りのPV」などに現れます。
ここで、\mu_e は elite なドキュメントの F_t の平均、\mu_{\overline{e}} は elite でないドキュメントの F_t の平均です。\mu_e は \mu_{\overline{e}} よりある程度大きいです。
これが2ポアソンモデルと呼ばれます。{\color{red} \mu_e = 3}, \color{blue} \mu_{\overline{e}} = 0.1 とすると、 g(f_t, \mu) はそれぞれ以下のようなグラフを描きます。
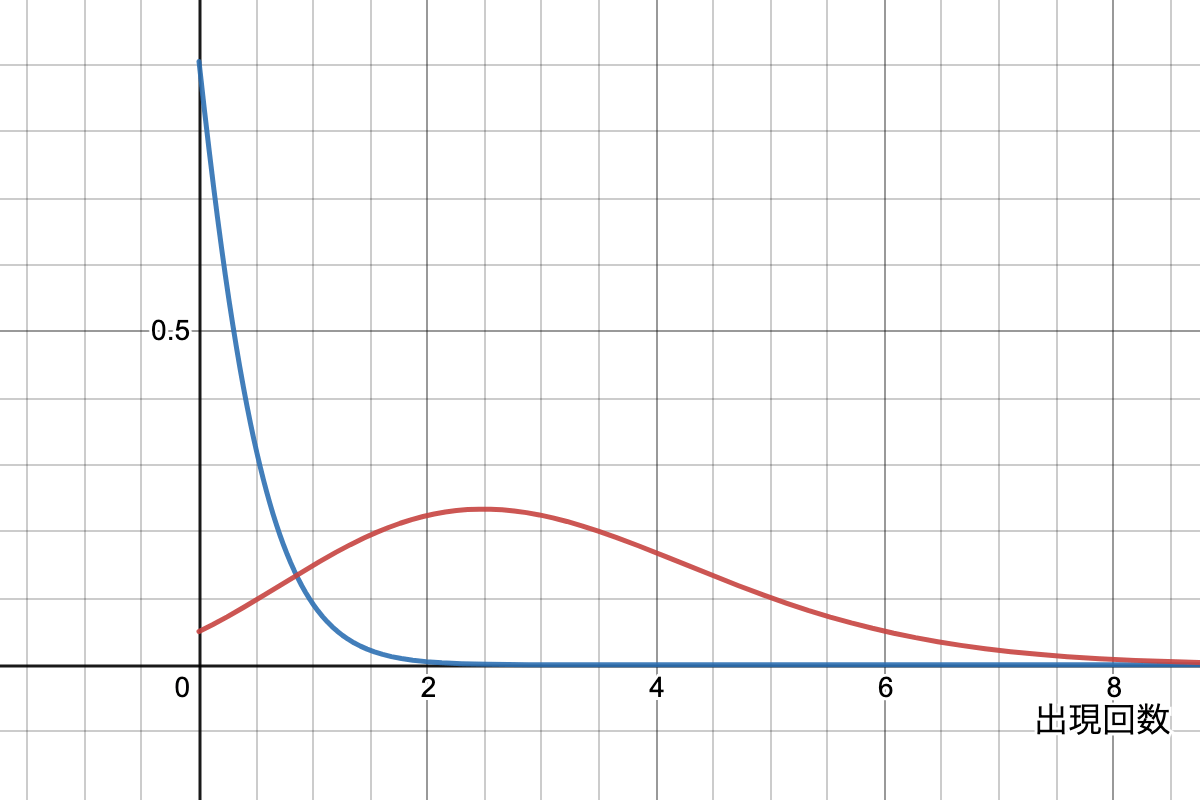
平均 \mu が 0 に近い場合、f_t = 0 のドキュメントが多く、単調減少になっています。一方で \mu がある程度以上の場合、\mu と \mu - 1 の間が最頻値となっている事がわかると思います。
では2ポアソンモデルとして w^f(f_t) を考えてみます。すると以下のような式が得られます。
w^f(f_t) =
log(
\scriptsize{
\dfrac{
(
g(f_t, \mu_e) p(e|r)+
g(f_t,\mu_{\overline{e}}) p(\overline{e}|r)
)
(
g(0,\mu_{e}) p(e|\overline{r})+
g(0,\mu_{\overline{e}}) p(\overline{e}|\overline{r})
)
}{
(
g(f_t,\mu_{e}) p(e|\overline{r})+
g(f_t,\mu_{\overline{e}}) p(\overline{e}|\overline{r})
)
(
g(0,\mu_{e}) p(e|r)+
g(0,\mu_{\overline{e}}) p(\overline{e}|r)
)
}
})
この目が潰れそうな式を見てもイメージがつかないと思うので、一例をグラフにしてみました。パラメーターは適当なので現実とは異なるかもしれないです。
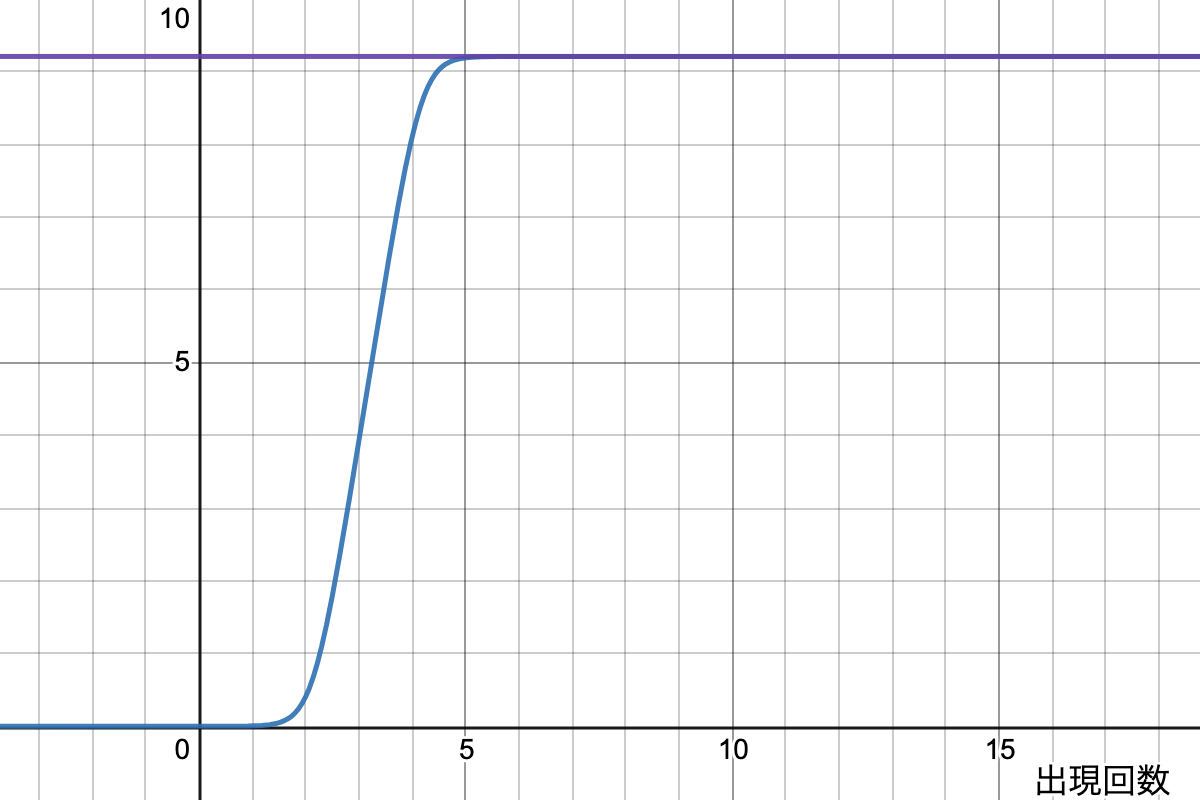
この w^f(f_t) は以下の特徴があります。
-
f_t = 0 の場合 0 になる
-
f_t に対して単調増加
-
f_t が無限になると w_t に近づく
2ポアソンモデルの近似
この特性を活かして簡略化した近似式を BM25 では採用しています。
w^f(f_t) = \frac{f_t}{k + f_t}w_t
この左側は従来の TF に相当します。従来の TF と違い、上限 1 に向かって増加する関数になっている点が異なります。k は [1, 2) の固定パラメーターで、1.2 が使われる事が多いようです。
この式をグラフにすると、下図の赤線のようになります。
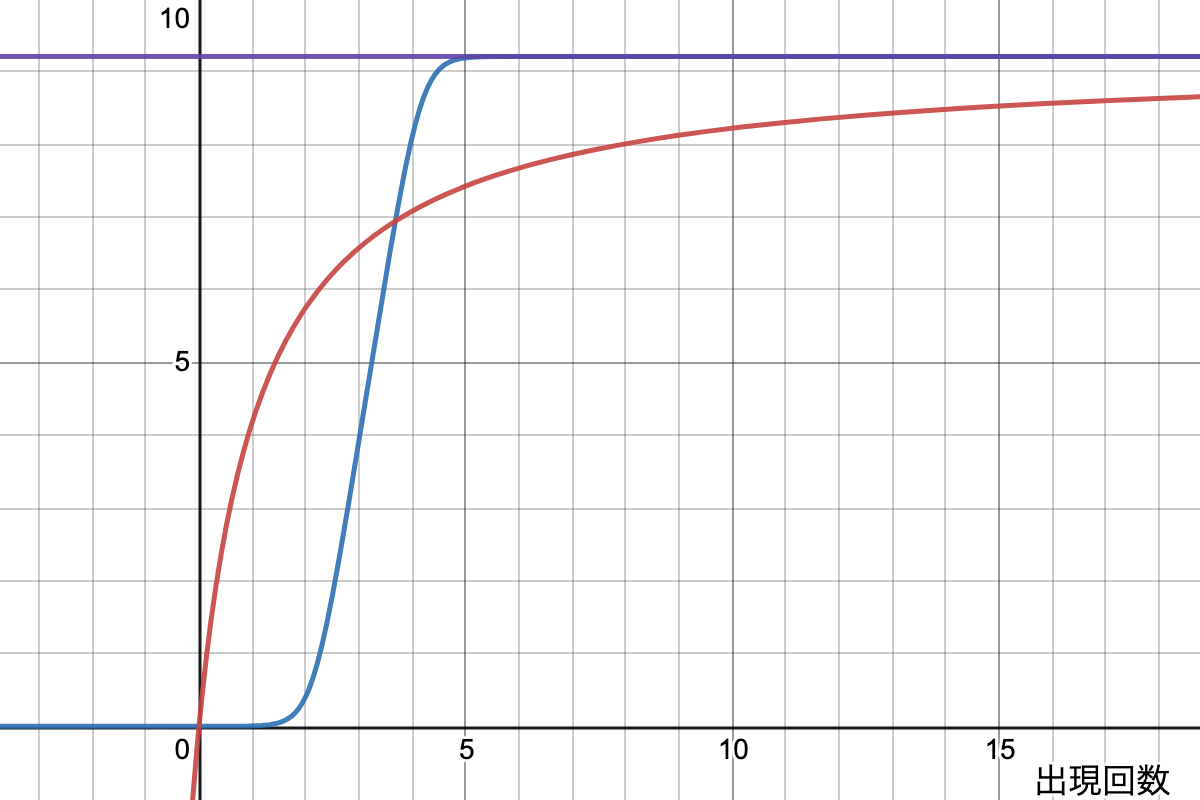
これで、出現頻度をスコアに変換する事ができるようになりました。
ドキュメントの長さの考慮
最後は課題4のドキュメント長に対する BM25 の解決方法についてです。「aの出現数が2倍、文章の長さが4倍」のようなドキュメントがあった時に、上の式では単に f_t が二倍で計算されます。しかし文章が4倍だった場合も同じように計算して良いのでしょうか?
BM25 ではドキュメントが長くなるのは二つの理由があるとしています。
- t についてより多くの内容を書いている
- t についての内容は変わらないが、細かく書いている
1. を仮定した場合、出現回数が多ければ f_t もそれに応じて高くするのが望ましいです。一方で、2. を仮定した場合、出現回数自体ではなくドキュメントの長さで割ったものを f_t として設定するのが望ましいです。
BM25 ではこの二種類の f_t を混合した値を使います。
f'_t = \frac{f_t}{(1 - b) + b(\dfrac{l}{l_{avg}})}
ここで、b は[0,1]の値、l はドキュメントの長さ、l_{avg} は検索対象のドキュメントの平均長です。この式をよく見ると以下の事がわかると思います。
-
b = 0 であれば f'_t = f_t
-
b = 1 であれば f'_t = (l_{avg} / l) f_t
-
l = l_{avg} であれば f'_t = f_t
一般的に b は 0.75 が使われます。
これを組み込むと、スコアは以下になります。
\LARGE{\sum_{i ∈ q} w^f(f_i) = \sum_{i ∈ q} \frac{f_i}{k((1 - b) + b(l/l_{avg})) + f_i}w_i}
これが最終的な BM25 の式になります。
BM25 でカバーできない問題
上の課題のうち、課題1〜課題4までは BM25 でカバーができました。一方で、課題5と課題6に関しては BM25 では解決できていません。一般的には以下の手法でカバーされる事が多いです。
明言されない関連キーワードの問題
クエリに対する関連キーワードを抽出し、それを使ってさらに検索するクエリ拡張(query expansion)という手法が使われます。これにより、直接クエリには含まれていない関連ドキュメントを取得する事ができるようになり、検索の性能が大きく向上する事が知られています。
この手法は BIM の限界を補填する方法ではある一方で、各タームの出現が独立であるという考えと矛盾する形とも言えます。また、平均的には性能が向上するものの、クエリによっては拡張される単語に引きずられ、性能が下がってしまう事がある事(query drift)も知られています。
クエリ拡張に関しては、情報検索の8章に詳しく書かれてあります。
クエリに無い要求の考慮
例えば人気のドキュメントを優先表示したいのケースがあります。
こういった場合、スコアにその他の要素によるスコアを加える手法が提案されています。例えば BM25 のスコアに log(PageRank()) を加えるといった事が考えられます。
前回の BIM に則れば、独立な二値の要素 b であればロバートソン/スパルクジョーンズ重み付け関数をスコアとして追加する事ができるでしょう。
\begin{align*}
w_b = &log(\dfrac
{\color{limegreen} p(b=1 | r)p(b=0 | \overline{r})}
{\color{red} p(b=1 | \overline{r})p(b=0 | r)}
)\\
w_b = &log(\dfrac{N}{n_b}) &… (r \sf が見積もれない場合)
\end{align*}
また、PV などの数値 x をスコアに加える場合は eliteness と 2 ポアソンモデルを仮定して飽和関数 x/(1+x)・w を加える事も妥当な選択肢と言えそうです。
まとめ
以上が BM25 の解説です。
多数のヒューリスティックスが入っているものの、確率の枠組みの中で採用されています。そのためか BM25 は計算のしやすさや拡張しやすさを維持しつつ、そこそこの検索結果を返すものとして現在でも多くのケースで採用されています。



Discussion