感染拡大モデルをシミュレーションする（SIRモデル）

動機

数理モデルでコロナ感染者などの拡大を予測できるのは有名ですが、
インタラクティブに作ってる人がいなかったのでNextjsで作りました。

SIRモデルとは

未感染者（S）、感染者（I）、免疫保持者（R）
と定義すると以下の関係が導かれます。

感染率係数をβ、回復率γと定義するとき、
未感染者は一定の確率で感染者となり、
感染者は一定の確率で免疫保持者になるということをここで示しています。

SIRモデルとは、こちらを数式化したものとなります。

$$\begin{aligned} \frac{dS}{dt} &= -\beta SI \\ \frac{dI}{dt} &= \beta SI - \gamma I \\ \frac{dR}{dt} &= \gamma I \end{aligned}$$

数学の分野では一般的に常微分方程式といいます。

📚 補足：常微分方程式とは？

常微分方程式とは何でしょうか？
例えば自然対数の底eのx乗を常微分方程式形式で書くとわかりやすいです。

「変化の速さ」が「今の値」と同じなので

$$\frac{d(e^x)}{dx} = e^x$$

このように書けます。yに置き換えるとこれがまさに

$$\frac{dy}{dx} = y$$

こちらが↑自然対数の底eのx乗の常備文形式となります。

$$y = e^x$$

補足からも推測できるように、S,I,Rはそれぞれ関数です。
なぜそれを最初から関数形式で書かないのでしょうか？。

結論から言うとSIRモデルは解が存在しません。つまり解くことができません。
逆を言えば解くことができない関数についても微分形式で表現できるところが常微分方程式の良いところと言えるでしょう。

📚 補足：SIRモデルの意味

こちらの式の意味をもう少し補足します。

$$\begin{aligned} \frac{dS}{dt} &= -\beta SI \\ \frac{dI}{dt} &= \beta SI - \gamma I \\ \frac{dR}{dt} &= \gamma I \end{aligned}$$

• 未感染者(S)の増減の速さ = - β × 未感染者数(S) × 感染者数(I)
  • 未感染者数は感染率や感染者数に応じて減っていくことがわかります
• 感染者(I)の増減の速さ = β × 未感染者数(S) × 感染者数(I) - γ × 感染者数(I)
  • 感染者数は感染率や感染者数に応じて増えていき、回復者に応じて減っていくことがわかります
• 回復者(R)の増減の速さ = γ × 感染者数(I)

サンプル

動画

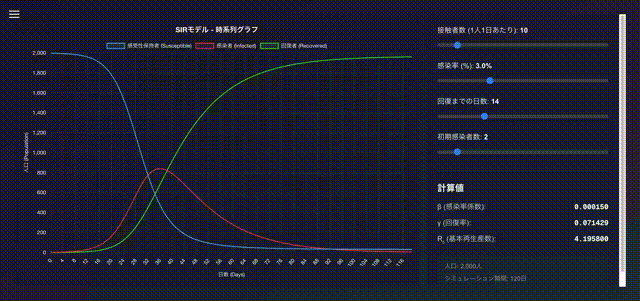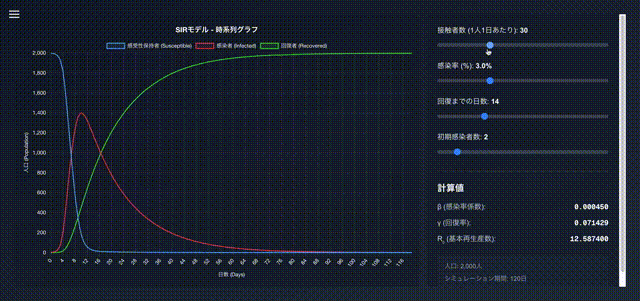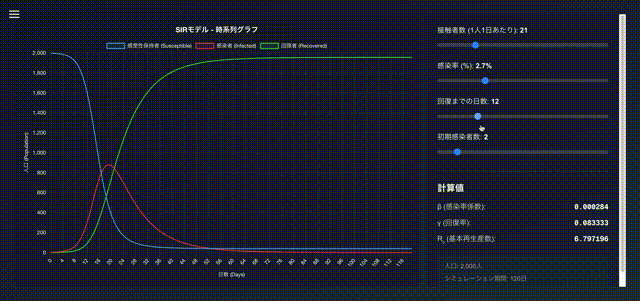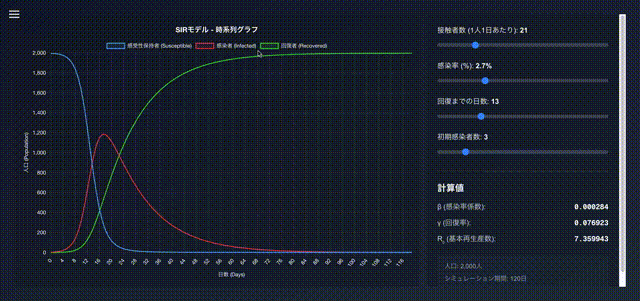
成果物

https://sir-dynamic-simulation-by-nextjs.vercel.app/works/sir-analytical

SIRモデルの数値解を求める

実は、解析的な解は導出できなくても、数値的な解は導出することができます。
代表的な方法としてルンゲクッタ法があります。時間変化t、未知変数yとしたとき

$$\begin{aligned} \frac{dy}{dt} = f(t, y) \end{aligned}$$

$$\begin{aligned} k_1 &= f(t, y) \\ k_2 &= f\left(t + \frac{dt}{2}, y + \frac{k_1}{2}\right) \\ k_3 &= f\left(t + \frac{dt}{2}, y + \frac{k_2}{2}\right) \\ k_4 &= f(t + dt, y + k_3) \\ y_{\text{new}} &= y + \frac{k_1 + 2k_2 + 2k_3 + k_4}{6} \cdot dt \end{aligned}$$

こちらが４次ルンゲクッタ法になります。

📚 補足：ルンゲクッタ法とは

微分方程式を数値的に解く方法のひとつです。

たとえば次のような常微分方程式を考えます。

$$\frac{dy}{dt} = f(t, y)$$

時間の経過とともに $y$ がどう変化するかを、
「少しずつ計算で追う」のが数値解法です。

---

⚙️ 例：落下するボールの速度

式：

$$\frac{dv}{dt} = g = 9.8$$

初期値：$v(0) = 0$

---

▶ オイラー法

ステップ幅 $h = 1$ 秒とすると、

$$v_{n+1} = v_n + h \cdot f(t_n, v_n)$$

1ステップ目：

$$v_1 = 0 + 1 \times 9.8 = 9.8$$

→ ずっと同じ傾きで進む。

---

▶ ルンゲクッタ法（4次）

ステップ幅 $h = 1$ の場合：

$$\begin{align} k_1 &= f(t_n, v_n) \\ k_2 &= f(t_n + \frac{h}{2}, v_n + \frac{h k_1}{2}) \\ k_3 &= f(t_n + \frac{h}{2}, v_n + \frac{h k_2}{2}) \\ k_4 &= f(t_n + h, v_n + h k_3) \\ v_{n+1} &= v_n + \frac{h}{6}(k_1 + 2k_2 + 2k_3 + k_4) \end{align}$$

傾きを4回見て、その重み付き平均をとって次の点を求めます。
$f=9.8$ が一定なら結果は同じですが、
$f$ が時間や状態で変わる場合は劇的に精度が上がります。

以下の関係に気をつけることで
SIRモデルを４次ルンゲクッタ法で
解くことができます！

$$y = \begin{pmatrix} S \\ I \\ R \end{pmatrix}, \quad f(t, y) = \begin{pmatrix} -\beta S I \\ \beta S I - \gamma I \\ \gamma I \end{pmatrix}$$

具体的ではないとわかりづらいと思います。

例えばk1を求めようとした時、

$$\begin{aligned} k_1 &= f(t, y) \end{aligned}$$

なので、

$$\begin{aligned} f(t, y) = \begin{pmatrix} -\beta SI \\ \beta SI - \gamma I \\ \gamma I \end{pmatrix} \end{aligned}$$

となり、

$$\begin{aligned} k_{1,S} &= -\beta SI \\ k_{1,I} &= \beta SI - \gamma I \\ k_{1,R} &= \gamma I \end{aligned}$$

このように定義できます。

コード中では時間発展を考慮するのでこのようになります。

// k1の計算
const k1_s = dt * f1(S,I,β);           // k₁,S = dt × (-βSI)
const k1_i = dt * f2(S,I,β,γ);    // k₁,I = dt × (βSI - γI)
const k1_r = dt * f3(I,γ);                // k₁,R = dt × (γI)

// SIRモデルの３式
const f1 = (S:number,I:number,β:number) => {
return -β * S * I
}
const f2 = (S:number,I:number,β:number,γ:number) => {
return β * S * I - γ * I 
}
const f3 = (I:number,γ:number) => {
return γ * I
}

k2,k3,k4についても

$$\begin{aligned} k_1 &= f(t, y) \\ k_2 &= f\left(t + \frac{dt}{2}, y + \frac{k_1}{2}\right) \\ k_3 &= f\left(t + \frac{dt}{2}, y + \frac{k_2}{2}\right) \\ k_4 &= f(t + dt, y + k_3) \\ y_{\text{new}} &= y + \frac{k_1 + 2k_2 + 2k_3 + k_4}{6} \cdot dt \end{aligned}$$

あとは↑こちらに倣って計算するだけです。

数値的に解くコード例（全体）

/**
 * dS/dt = -β * S * I
 * @param beta 解析的モデルの感染率係数（人口スケール）
 */
function f1(s: number, i: number, beta: number): number {
    return -1 * beta * s * i;
}

/**
 * dI/dt = β * S * I - γ * I
 * @param beta 解析的モデルの感染率係数（人口スケール）
 */
function f2(
    s: number,
    i: number,
    beta: number,
    gamma: number,
): number {
    return beta * s * i - gamma * i;
}

/**
 * dR/dt = γ * I
 */
function f3(i: number, gamma: number): number {
    return gamma * i;
}

/**
 * 4次ルンゲクッタ法でSIRモデルを解く
 */
export function solveSIR(params: SirParameters): SirResult {
    const {
        population,
        contactPerDay,
        infectionRate,
        recoveryDays,
        initialInfected,
        maxDays,
        dt,
    } = params;

    // 計算式:
    // β_analytical = (感染率/100 × 接触者数) / 人口
    // γ = 1 / 回復日数
    const beta = ((infectionRate / 100) * contactPerDay) / population;
    const gamma = 1.0 / recoveryDays;

    // 初期状態
    let s = population - initialInfected;
    let i = initialInfected;
    let r = 0;

    // 結果を格納する配列
    const timeArray: number[] = [];
    const sArray: number[] = [];
    const iArray: number[] = [];
    const rArray: number[] = [];

    // ルンゲクッタ法のメインループ
    for (let t = 0; t < maxDays; t += dt) {
        // 現在の状態を記録
        timeArray.push(t);
        sArray.push(s);
        iArray.push(i);
        rArray.push(r);

        // k1の計算
        const k1_s = dt * f1(s, i, beta);
        const k1_i = dt * f2(s, i, beta, gamma);
        const k1_r = dt * f3(i, gamma);

        // k2の計算
        const k2_s = dt * f1(s + k1_s / 2.0, i + k1_i / 2.0, beta);
        const k2_i = dt *
            f2(s + k1_s / 2.0, i + k1_i / 2.0, beta, gamma);
        const k2_r = dt * f3(i + k1_i / 2.0, gamma);

        // k3の計算
        const k3_s = dt * f1(s + k2_s / 2.0, i + k2_i / 2.0, beta);
        const k3_i = dt *
            f2(s + k2_s / 2.0, i + k2_i / 2.0, beta, gamma);
        const k3_r = dt * f3(i + k2_i / 2.0, gamma);

        // k4の計算
        const k4_s = dt * f1(s + k3_s, i + k3_i, beta);
        const k4_i = dt * f2(s + k3_s, i + k3_i, beta, gamma);
        const k4_r = dt * f3(i + k3_i, gamma);

        // 次の状態を計算
        s = s + (k1_s + 2.0 * k2_s + 2.0 * k3_s + k4_s) / 6.0;
        i = i + (k1_i + 2.0 * k2_i + 2.0 * k3_i + k4_i) / 6.0;
        r = r + (k1_r + 2.0 * k2_r + 2.0 * k3_r + k4_r) / 6.0;
    }

    return {
        time: timeArray,
        susceptible: sArray,
        infected: iArray,
        recovered: rArray,
    };
}

こちらのデータセットはreact-chartjs-2を使ってグラフ描画しました。
（以下resultが上記のデータセット）

'use client';

import {
  CategoryScale,
  Chart as ChartJS,
  Legend,
  LinearScale,
  LineElement,
  PointElement,
  Title,
  Tooltip,
} from 'chart.js';
import { Line } from 'react-chartjs-2';
import type { SirResult } from '../types/sir-analytical-types';

// Chart.jsの登録
ChartJS.register(
  CategoryScale,
  LinearScale,
  PointElement,
  LineElement,
  Title,
  Tooltip,
  Legend,
);

interface AnalyticalChartProps {
  result: SirResult;
}

export function AnalyticalChart({ result }: AnalyticalChartProps) {
  const data = {
    labels: result.time,
    datasets: [
      {
        label: '感受性保持者 (Susceptible)',
        data: result.susceptible,
        borderColor: 'hsl(210 80% 60%)',
        backgroundColor: 'hsl(210 80% 60% / 0.1)',
        borderWidth: 2,
        pointRadius: 0,
        tension: 0.1,
      },
      {
        label: '感染者 (Infected)',
        data: result.infected,
        borderColor: 'hsl(0 80% 60%)',
        backgroundColor: 'hsl(0 80% 60% / 0.1)',
        borderWidth: 2,
        pointRadius: 0,
        tension: 0.1,
      },
      {
        label: '回復者 (Recovered)',
        data: result.recovered,
        borderColor: 'hsl(120 60% 45%)',
        backgroundColor: 'hsl(120 60% 45% / 0.1)',
        borderWidth: 2,
        pointRadius: 0,
        tension: 0.1,
      },
    ],
  };

  const options = {
    responsive: true,
    maintainAspectRatio: false,
    plugins: {
      legend: {
        position: 'top' as const,
        labels: {
          color: '#ffffff',
          font: {
            size: 12,
          },
        },
      },
      title: {
        display: true,
        text: 'SIRモデル - 時系列グラフ',
        color: '#ffffff',
        font: {
          size: 16,
        },
      },
    },
    scales: {
      x: {
        title: {
          display: true,
          text: '日数 (Days)',
          color: '#ffffff',
        },
        ticks: {
          color: '#ffffff',
        },
        grid: {
          color: 'rgba(255, 255, 255, 0.1)',
        },
      },
      y: {
        title: {
          display: true,
          text: '人口 (Population)',
          color: '#ffffff',
        },
        ticks: {
          color: '#ffffff',
        },
        grid: {
          color: 'rgba(255, 255, 255, 0.1)',
        },
      },
    },
  };

  return (
    <div className="w-full h-full">
      <Line data={data} options={options} />
    </div>
  );
}