Zenn
🐈

Binance永久先物の5秒足クローズとその7日間移動平均の乖離と戯れる

2022/11/02に公開
#
仮想通貨
tech

きっかけ

https://zenn.dev/wannabebotter/articles/7a521e8ec2ea36 で移動平均と戯れて、5秒足でも1時間足でも7日間移動平均の取る値は大体同じということがわかったので、次は5秒足のクローズ価格とその7日間移動平均との乖離と戯れることにしました。

リアルな価格乖離が出てくると、だいぶBotっぽくなってきますね。

やること

  • BTCUSDTとETHUSDTについて、5秒足クローズとその7日間移動平均の間の乖離がどのような振る舞いを示すかを調べます。

コード

コードサンプルは以下の通りです。

timebar_exercise3.ipynb
import pandas as pd
import numpy as np
import statsmodels
import matplotlib.pyplot as plt
import japanize_matplotlib
from tqdm.auto import tqdm
import exercise_util

#target_symbols = list(exercise_util.target_symbols.keys())
target_symbols = ['BTCUSDT', 'ETHUSDT']

cols = 3
rows = len(target_symbols)
fig, axs = plt.subplots(rows, cols, figsize = (9 * cols, 7 * rows))

str_start = '2020-01-01'

for _idx, _symbol in tqdm(enumerate(target_symbols), total = len(target_symbols)):
    df_5sec = exercise_util.concat_timebar_files(_symbol, 5, str_start)

    df_5sec['close_7days_mean'] = df_5sec['close'].rolling(7 * 24 * 60 * 60 // 5).mean()

    df_5sec.dropna(inplace = True)

    _ax = axs[_idx, 0]
    _ax.tick_params(axis = 'x', labelrotation = 45)
    _ax.plot(df_5sec['close'], label = 'df_5sec.close', lw = 0.5)
    _ax.plot(df_5sec['close_7days_mean'], label = 'df_sec.close_7days_mean', lw = 0.5)
    _ax.legend()
    _ax.set_title(f'{_symbol} クローズと移動平均)')

    _log_close = np.log(df_5sec['close'])
    _close_ma_deviation = _log_close - np.log(df_5sec['close_7days_mean'])
    _ax = axs[_idx, 1]
    _ax.tick_params(axis = 'x', labelrotation = 45)
    _ax.plot(_close_ma_deviation, label = 'df_sec.close_7days_mean_deviation', lw = 0.5)
    _ax.legend()
    _ax.set_title(f'{_symbol} クローズと移動平均の乖離率)')

    _ax = axs[_idx, 2]
    _ax.hist(_close_ma_deviation, bins = 100, density = True)
    _mean = _close_ma_deviation.mean()
    _std = _close_ma_deviation.std()
    _ax.axvline(_mean, linestyle = 'dotted', color = 'red')
    _ax.axvline(_mean + _std, linestyle = 'dotted', color = 'red')
    _ax.axvline(_mean + -1 * _std, linestyle = 'dotted', color = 'red')
    _ax.axvline(_mean + 2 * _std, linestyle = 'dotted', color = 'red')
    _ax.axvline(_mean + -2 * _std, linestyle = 'dotted', color = 'red')
    _ax.axvline(_mean + 3 * _std, linestyle = 'dotted', color = 'red')
    _ax.axvline(_mean + -3 * _std, linestyle = 'dotted', color = 'red')

    _ax.axvline(_close_ma_deviation.quantile(0.5), linestyle = 'dotted', color = 'blue')
    _ax.axvline(_close_ma_deviation.quantile(0.5 - 0.6827 / 2), linestyle = 'dotted', color = 'blue')
    _ax.axvline(_close_ma_deviation.quantile(0.5 + 0.6827 / 2), linestyle = 'dotted', color = 'blue')
    _ax.axvline(_close_ma_deviation.quantile(0.5 - 0.9545 / 2), linestyle = 'dotted', color = 'blue')
    _ax.axvline(_close_ma_deviation.quantile(0.5 + 0.9545 / 2), linestyle = 'dotted', color = 'blue')
    _ax.axvline(_close_ma_deviation.quantile(0.5 - 0.9973 / 2), linestyle = 'dotted', color = 'blue')
    _ax.axvline(_close_ma_deviation.quantile(0.5 + 0.9973 / 2), linestyle = 'dotted', color = 'blue')

    _ax.set_title(f'{_symbol} クローズと移動平均の乖離率の分布 (青: 分位点ベース, 赤: 標準偏差ベース)')

fig.show()

コード全体はこちらです。
https://github.com/WannabeBotter/binance_exercise/blob/main/timebar_exercise_3.ipynb

結果

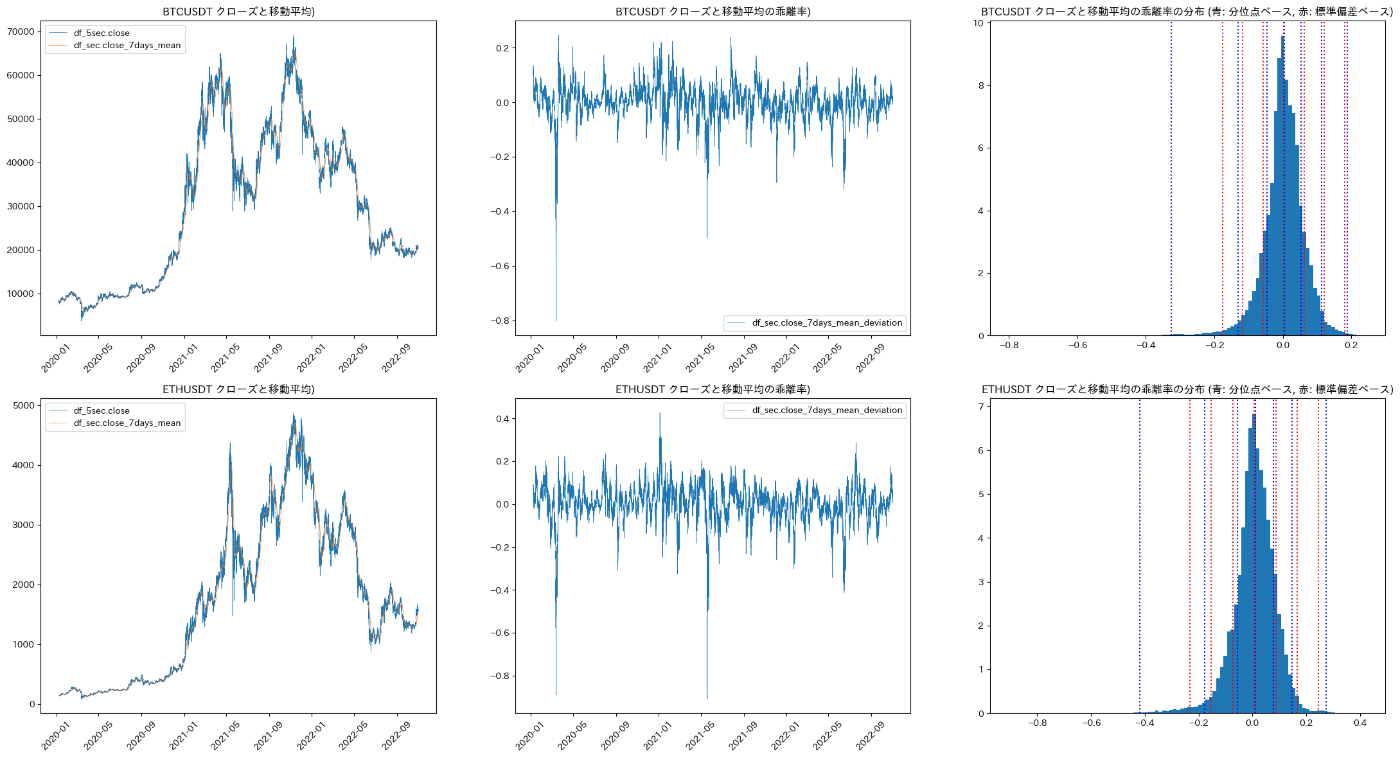左から、クローズ系列と移動平均線、クローズ系列と移動平均の乖離率、クローズ系列と移動平均の乖離率の分布

真ん中の図から、クローズ系列と移動平均の乖離率は定常性があるのは間違いなさそうです。であれば、移動平均線から一定量乖離したときに逆張りのトレードをすることで、ちょっとだけ有利なサイコロを振れるのかもしれません。

一番右の分布図では、クローズ系列と移動平均の乖離を表示していますが、それぞれ平均から \pm 1 \sigma, \pm 2 \sigma, \pm 3 \sigma の地点に赤の点線を、正規分布で \pm 1 \sigma, \pm 2 \sigma, \pm 3 \sigmaの分位点に相当する分位点 (67.27%, 95.45%, 99.73%)に青い点線を引いてみました。

ぱっと見、クローズ系列と移動平均の乖離の分布はマイナス側にテールが長くなっていることがわかります。クローズ系列と移動平均の価格乖離は、クローズ価格が移動平均に先行して下がっているとき、より大きく広がる傾向があるようです。

もう一つ、一番右の分布図からわかることは、乖離が思ったよりデカいことです。95%水準でもBTCUSDTでは15%くらい、ETHUSDTでは20%くらいの乖離になっていて、これはちょっと大きすぎるような…。今回は5秒足のクローズ価格を使ったのですが、これ一瞬の大きな価格乖離を捉えてしまうので、うすーい乖離が分布図で強調されてしまっているのかもしれません。

BTCやETHでボリンジャーバンドタッチを使って取引をする場合は、赤の点線で指値して、タッチしたときに逆張りで売買する形になりますが、ちょっと考えると以下のようになっていいところがなさそうです。

  • 乖離値が負側では、実際の分布に基づく青い点線が赤い点線より小さい値になっているので、ボリンジャーバンドで見るとクローズ価格は下がりすぎだ、と思って赤い点線でロングエントリーすると、ファットテールさんが起こす追加の価格下落でボコられそうです。
  • 一方、乖離値が正側では、実際の分布に基づく青い点線が赤い点線より小さい値になっているので、クローズ価格がボリンジャーバンドに下から近づいてきて、そろそろ逆張りショートしようかと思うと、スッと価格が反転下落していき、エントリーを逃しそうです。
  • そして、赤い点線と青い点線が近い価格乖離が小さい領域では、取引をすると手数料に負けそうです。

おわりに

クローズ系列と移動平均の乖離の大まかなイメージを掴むことができました。乖離に定常性がありそうというのはよい発見でした。

また、ボリンジャーバンドのような移動平均からの乖離が正規分布であることを仮定したシグナルは、乖離の分布が正規分布ではない仮想通貨ではうまく機能しないかもしれない…ということがわかりました。例えば、手数料負けを避けるために、3 \sigmaあたりの乖離をシグナルにして、一回の利幅の期待値を上げようとすると特に誤差が大きい領域に入ってしまい危ないでしょう。

移動平均からの乖離幅をシグナルに取引するならば、ボリンジャーバンドのような標準偏差を仮定した上下対称のシグナルを使うのではなく、直近N区間での実際の乖離分布から、分位点を使って上下非対称の指値幅を計算するほうがよいのかも？

ATRはどうなのかなぁ。

おまけ1

乖離と指値幅というと、マーケットメイキング理論がしっかりした数理的な最適解を求められる状態になっているようです。昔はさっぱりわかりませんでしたが今なら読んで理解できるかも？

ということで解説が書いてあるHohetoさんの昔のブログ記事をぺたっと貼っておきます。
https://we.love-profit.com/entry/2018/02/12/113916

おまけ2

今回負側にテールの広い定常性のある分布が出てきましたが、なんか内部状態 (乖離の大きさ) によって次の乖離率の変化が変わってきそうな感じが、ちょっとマルコフ過程っぽいなぁ…と思ってしまうのですが、マルコフ過程+定常時系列で検索したらなんかメジャーリーグの薬物云々と、読み物としても面白そうなPDFが出てきたので、これも貼っておきます。

コピュラ・マルコフ連鎖モデルによる定常時系列解析―パラメトリック推定と統計的工程管理―
江村　剛志
https://www.jstage.jst.go.jp/article/jjssj/51/1/51_41/_pdf

でもコピュラってなんぞ？　全然わからぬ…。

Discussion