📌
もう忘れないスターリングの公式

2025/05/05に公開
以下の形のスターリングの公式は有名です：

\begin{equation*} n! \sim \sqrt{2\pi n} \left( \frac{n}{e}\right)^n \end{equation*}
この公式はある程度精度が高く数理統計学や統計物理における漸近公式などに使用される一方で, ちゃんと示そうとする方法はいずれもそこそこ骨が折れ, \sqrt{2\pi n} という補正項を覚えていないとわからないことが多いという難点もあります.
この記事では, 前提知識をなるべく減らし, 上記の主要項をラフに導出する方法について述べます

 前提知識高校数学に加えて, 微積分の以下の事実を抑えておきます.
2次のテイラー展開：

\phi(x) \sim \phi(t) + \phi'(t)(x-t) + \dfrac{\phi''(t)}{2} (x-t)^2
階乗のガンマ関数による表示： n! = \Gamma(n+1) = \int_0^\infty x^n e^{-x}\,dx
平均 \mu\in \mathbf{R}, 分散 \sigma^2 >0 に対する正規分布におけるガウス積分：

\int_{-\infty}^\infty \exp{\dfrac{(x-\mu)^2}{2\sigma^2}}\, dx = \sqrt{2\pi \sigma^2}
(形式計算を受け入れるおおらかな心)

 形式計算まず, ガンマ関数を用いて積分により書き直します
 \begin{aligned}
n!
&= \Gamma(n+1)\\
&= \int_0^\infty x^n e^{-x}\,dx\\
&= \int_0^\infty \exp{(n\log x - x)}\,dx\\
&= \int_0^\infty \exp{\phi_n(x)}\,dx.
\end{aligned} ただしここで \phi_n(x)= n\log x - x とおきました. この関数は微分すると,

\phi'_n(x) = \dfrac{n}{x} -1 
により最大値は x = n で達成されます.
この関数を指数関数に含む定積分 \int_0^\infty \exp{\phi_n(x)}\,dx の主要部は x\sim n の部分となります[1].
x\sim t においては
　\begin{aligned}
\phi_n(x) &= n\log x - x \\&\sim n\log n -n,\\
\phi'_n(x) &=  \dfrac{n}{x} -1 \\&\sim 0,\\
\phi''_n(x) &=  -\dfrac{n}{x^2} \\&\sim -\dfrac{1}{n}
\end{aligned} という感じになります. このことから
\begin{aligned}
\phi_n(x) 
&\sim \phi(n) + \phi'(n)(x-n) + \dfrac{\phi''(n)}{2} (x-n)^2\\
&= n\log n -n - \dfrac{(x-n)^2}{2n}
\end{aligned} であり,
 \begin{aligned}
\int_0^\infty \exp{\phi_n(x)}\,dx
&\sim \int_0^\infty \exp{\left( n\log n -n - \dfrac{(x-n)^2}{2n}\right)}\, dx\\
& = \left(\dfrac{n}{e}\right)^n \int_0^\infty \exp{\dfrac{(x-n)^2}{2n}}\, dx
\end{aligned} が従います. ここで, 定積分 \int_0^\infty \exp{\frac{(x-n)^2}{2n}}\, dx の被積分関数は平均 n, 分散 n の正規分布であり, 平均 n\rightarrow \infty においては \int_{-\infty}^0 \exp{\frac{(x-n)^2}{2n}}\, dx はほとんど 0 だと信じると,

\int_0^\infty \exp{\dfrac{(x-n)^2}{2n}}\, dx \sim \sqrt{2\pi n}
を得ます. 以上の議論をまとめると,
 \begin{aligned}
n!
&= \int_0^\infty \exp{\phi_n(x)}\,dx\\
&\sim \left(\dfrac{n}{e}\right)^n \int_0^\infty \exp{\dfrac{(x-n)^2}{2n}}\, dx\\
&\sim \left( \frac{n}{e}\right)^n \sqrt{2\pi n}
\end{aligned} が得られました.

 積分が漸近する様子の可視化上記の議論においては,

x^n e^{-x}  = \exp{\phi_n(x)}
の定積分は 【 \exp{\phi_n(x)} の最大値】×【分散 n の正規分布】であることをアイデアとして用いました.
被積分関数を Python で可視化すると, 以下のような gif が得られます：
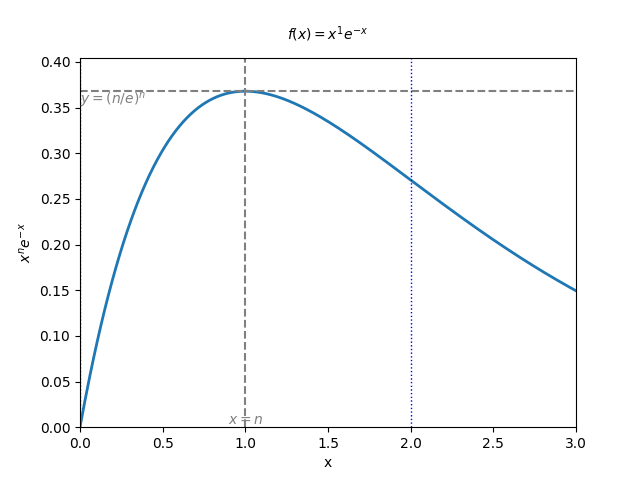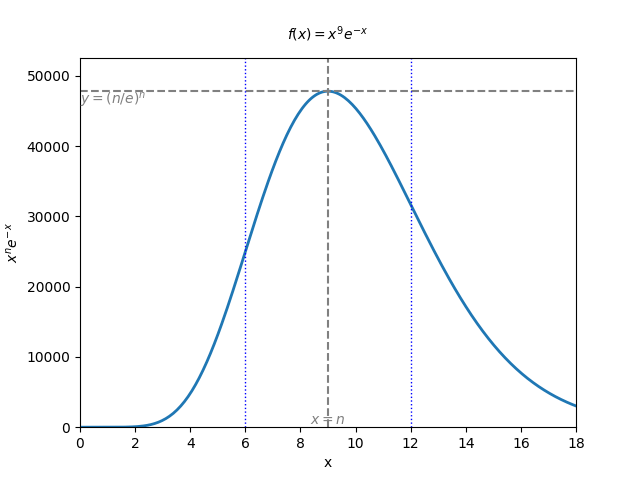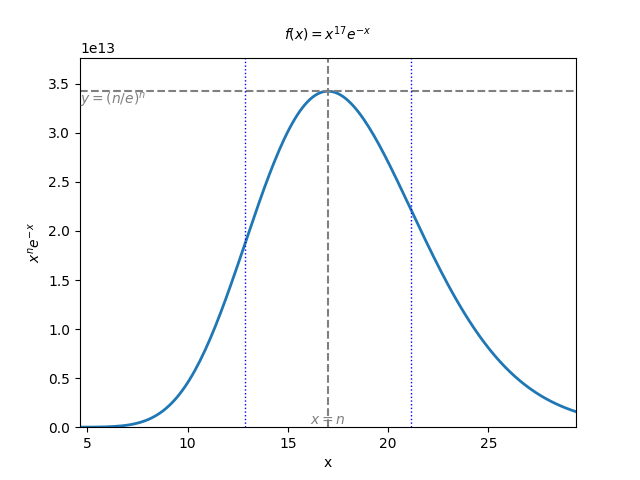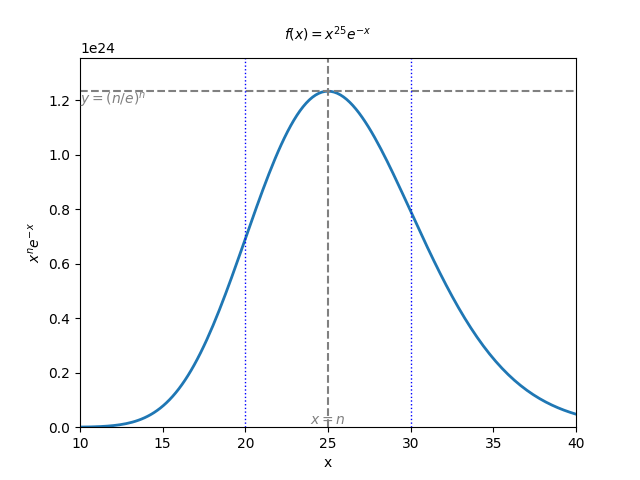
漸近の仕方は左右対称ではないものの, 形式計算における 【\exp{\phi_n(x)}の最大値】×【分散 n の正規分布】というアイデアは近似になっていることが見て取れます.
Google Colaboratory で以下を用いると, 手元の環境でも試すことができます
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
from IPython.display import HTML

# 初期化
fig, ax = plt.subplots()
line, = ax.plot([], [], lw=2)
vline = ax.axvline(x=0, color='gray', linestyle='--')  # 破線の初期化
hline = ax.axhline(y=0, color='gray', linestyle='--')  # 破線の初期化
title = ax.text(0.5, 1.05, "", transform=ax.transAxes, ha="center")
ax.set_xlabel("x")
ax.set_ylabel(r"$x^n e^{-x}$")
x_label = ax.text(0, 0, "", ha='center', va='bottom', fontsize=10, color='gray')
y_label = ax.text(0, 0, "", ha='left', va='top', fontsize=10, color='gray')
sigma_minus = ax.axvline(x=0, color='blue', linestyle=':', lw=1)
sigma_plus = ax.axvline(x=0, color='blue', linestyle=':', lw=1)

# 初期化関数
def init():
    line.set_data([], [])
    vline.set_xdata([0])
    hline.set_ydata([0])
    title.set_text("")
    x_label.set_text("")
    x_label.set_position((0, 0))
    y_label.set_text("")
    y_label.set_position((0, 0))
    sigma_minus.set_xdata([0])
    sigma_plus.set_xdata([0])
    return line, vline, title

# 更新関数
def update(n):
    x = np.linspace(0, 3 * n, 400)
    y = x**n * np.exp(-x)
    line.set_data(x, y)
    sigma = np.sqrt(n)
    sigma_minus.set_xdata([n - sigma])
    sigma_plus.set_xdata([n + sigma])
    xmin = max(0, n - 3 * sigma)
    xmax = min(3 * n, n + 3 * sigma)
    vline.set_xdata([n])
    x_label.set_position((n, 0))
    x_label.set_text(rf"$x = n$")
    hline.set_ydata([(n/np.e)**n])
    y_label.set_position((xmin, (n/np.e)**n))
    y_label.set_text(rf"$y = (n/e)^{{n}}$")
    ax.set_xlim(xmin, xmax)
    ax.set_ylim(np.min(y), np.max(y) * 1.1)
    title.set_text(rf"$f(x) = x^{{{n}}} e^{{-x}}$")
    return line, vline, title


# アニメーション作成
ani = FuncAnimation(fig, update, frames=range(1, 26),
                    init_func=init, blit=True, interval=500)

# Colab からのダウンロード
from google.colab import files
ani.save("xn_exp_minus_x.gif", writer="pillow", fps=2)
files.download("xn_exp_minus_x.gif")

 リンクスターリングの近似 - Wikipedia

脚注
指数関数に n が乗っていることから, x\nsim n における積分への寄与が急激に小さくなることが原因だが、形式計算なのであまり意識しなくて良い ↩︎
前提知識

形式計算

積分が漸近する様子の可視化

リンク

Discussion
