非線形システムの最適制御を勾配法のJAX実装で解く

はじめに

https://www.coronasha.co.jp/np/isbn/9784339033182/

の7.2節の勉強ノートです.

https://zenn.dev/takuya_fukatsu/articles/0b9c8df4a51042

によるとJAXにより非線形最適制御が効率良く解けるとのことだったので, シンプルな勾配法（最急降下法・共役勾配法）での実装にチャレンジしてみました！

問題設定

状態ベクトルの次元 $n=2$, 入力制御ベクトルの次元 $m=1$ とし, 線形システム

$$\dot{x}(t) = f(x(t),u(t)), \quad t\in (0,T)$$

を考えます. ここで最終時刻は $T=4$ とし, 関数 $f$ は以下のような非線形性を持つものとします

$$f(x,t) = \begin{bmatrix} x_2\\ 2x_1(1-x_1^2) -x_2 + u \end{bmatrix}.$$

初期値は

$$x(0)=\begin{bmatrix} 0.5\\ 0\end{bmatrix}$$

とします. 評価関数は

$$J=\dfrac12 x^T(T) S_fx(T) + \dfrac12\int_0^T L(x(t), u(t))\, dt$$

において

$$L(x,t) = x^TQx + u^TRu,\quad S_f=Q=\begin{bmatrix} 13& 0\\ 0&1\end{bmatrix},\quad R=\begin{bmatrix} 1 \end{bmatrix}$$

とします. すなわち

$$J=\dfrac12 \left(13x_1(T)^2 + x_2(T)^2 \right) +\dfrac12 \int_0^T\left(13x_1(t)^2 + x_2(t)^2 +u(t)^2\right)\, dt.$$

を最小化する最適制御を考えます.

制御入力がない場合

まず, 制御入力を与えない場合( $u=0$ )のダイナミクスを明らかにします

パラメータ設定

共通のパラメータはグローバル変数として定義しておきます

import jax
import jax.numpy as jnp

# 問題設定
S_f = jnp.array([[13, 0], [0, 1]], dtype=float)
Q = jnp.array([[13, 0], [0, 1]], dtype=float)
R = jnp.array([[1]], dtype=float)

x_0 = jnp.array([[0.5], [0]], dtype=float)

# 解く区間
t0, t1 = 0, 4
dt = 0.01

評価関数の定義

@jax.jit
def compute_J(x, u):
    N = x.shape[0]
    dt_ = (t1 - t0) / N

    x_T = x[-1]  # 最後の時刻の状態, 形状は (n, 1)
    terminal_cost = 0.5 * jnp.matmul(x_T.T, jnp.matmul(S_f, x_T)).squeeze()

    xQx = jnp.einsum("nkj,ki,nij->n", x, Q, x)  # 形状は (N,)
    uRu = jnp.einsum("nkj,ki,nij->n", u, R, u)  # 形状は (N,)
    integral_cost = 0.5 * jnp.sum(xQx + uRu) * dt_

    J = terminal_cost + integral_cost
    return J

diffrax で常微分方程式を解く際の共通設定

常微分方程式はJAXベースの微分方程式ソルバー提供ライブラリである diffraxを使用します

import diffrax

N = 1000
ts = jnp.linspace(t0, t1, N)
solver = diffrax.Tsit5()
saveat = diffrax.SaveAt(ts=ts)

状態方程式の定義

@jax.jit
def function_f(x, u):
    """状態方程式における f"""
    x1, x2 = x
    u1 = u.squeeze()
    return jnp.array([x2, -2 * (x1**3) + 2 * x1 - x2 + u1], dtype=float)


def vector_field_x(t, x, args):
    u_t = args.evaluate(t)
    return function_f(x, u_t)


state_eq = diffrax.ODETerm(vector_field_x)

制御入力に対する状態ベクトルの可視化

状態ベクトル $X(t)=(x(t),\dot{x}(t))$ を左のグラフに配置し, 制御入力を右のグラフに配置します.

制御入力がない場合, 安定平衡点 $(1,0)$ に漸近することがわかります

import matplotlib.pyplot as plt


def plot_control(u):
    # u を与えて状態方程式の解 x を求める
    u_func = diffrax.LinearInterpolation(ts=ts, ys=u)
    sol = diffrax.diffeqsolve(state_eq, solver, t0, t1, dt, x_0, args=u_func, saveat=saveat)
    x = sol.ys

    X = jnp.array(x).reshape(N, 2)
    U = jnp.array(u).reshape(N, 1)

    plt.figure(figsize=(12, 4))

    plt.subplot(1, 2, 1)
    for k in range(2):
        plt.plot(ts, X[:, k], label=f"x_{k}")
    plt.axhline(1, color="blue", linestyle="--", linewidth=0.7)
    plt.axhline(0, color="black", linestyle="--", linewidth=0.7)
    plt.ylim(-0.5, 1.2)
    plt.legend()

    plt.subplot(1, 2, 2)
    for k in range(1):
        plt.plot(ts, U[:, k], linestyle="--", label="u")
    plt.axhline(0, color="black", linestyle="--", linewidth=0.7)
    plt.ylim(-3.0, 0.2)
    plt.legend()
    plt.show()

    score = float(compute_J(x, u))
    print(f"{score=}")

u = jnp.zeros((N, 1, 1))
plot_control(u)

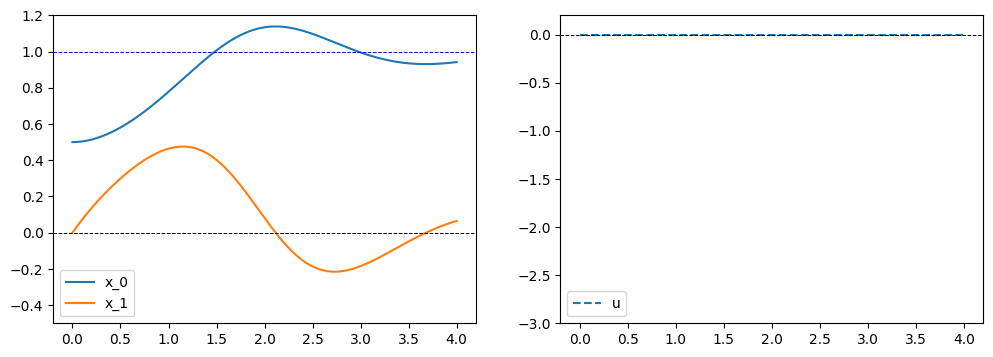
score=28.224021911621094

オイラー・ラグランジュ方程式

ハミルトニアンを $H(x,u,\lambda)=L(x,u)+\lambda^T f(x,u)$ とおきます. このときオイラー・ラグランジュ方程式は

$$\begin{aligned} &\dot{x}(t) = f(x(t), u(t)), \quad x(0)=x_0, \\ &\dot{\lambda}(t) = -\left(\dfrac{\partial H}{\partial x}\right)^T (x(t), u(t), \lambda(t)) , \quad \lambda(T) = S_f (x(T)), \\ &\dfrac{\partial H}{\partial u}(x(t),u(t),\lambda(t))=0 \end{aligned}$$

となります.

第一式を状態方程式, 第二式を随伴方程式と言います. 拘束条件を表す第三式は本記事では以降は明示的に使用しません.

最急降下法

以下のアルゴリズムにより最適制御を求めます

1. 適当な $u$ を制御入力の初期推定解とする
2. $u$ を用いて状態方程式を解いて $x$ を, 随伴方程式を解いて $\lambda$ を求める
3. $x$, $u$, $\lambda$ から $\frac{\partial H}{\partial u}$ を計算する.
4. $s=-\left(\frac{\partial H}{\partial u}\right)^T$ とおく
5. 制御入力を $u+\alpha s$ としたときの評価関数値 $J[u+\alpha s]$ が最小になるスカラー $\alpha$ を求め, $u=u+\alpha s$ と更新してステップ2に戻る
   • ただし, 以下の条件を満たす場合は収束したとみなす
     • 勾配のノルム $\left(\int_{0}^{T}\left\|s(t)\right\|^2\, dt\right)^{\frac{1}{2}}$ が十分小さい再場合
     • 制御の変更のノルム $\alpha \left(\int_{0}^{T}\left\|s(t)\right\|^2\, dt\right)^{\frac{1}{2}}$ が十分小さい場合

随伴方程式の定義

ハミルトニアンの偏微分を用いて書けることから, 自動微分を用いて定義します.

また, 時間逆方向に解くので符号を逆転しておきます.

@jax.jit
def hamiltonian(x, u, lambda_):
    L = 0.5 * (jnp.matmul(x.T, jnp.matmul(Q, x)) + jnp.matmul(u.T, jnp.matmul(R, u)))
    f = function_f(x, u)
    H = L + jnp.matmul(lambda_.T, f)
    return H.squeeze()


grad_H_x = jax.grad(hamiltonian, argnums=0)


def vector_field_lambda(t, lambda_, args):
    x_t = args[0].evaluate(t)
    u = args[1].evaluate(t)
    dot_lambda = grad_H_x(x_t, u, lambda_)
    return dot_lambda


lambda_eq = diffrax.ODETerm(vector_field_lambda)

目的関数の勾配計算

制御入力に対する変分として, ハミルトニアンの勾配を用いるのでこちらも自動微分を用いて定義します.

直線探索の最適値 $\alpha\in (0,1)$ を求めるために scipy.optimize.minimize_scalar を使用するため, 制御入力に対応する評価関数を計算できるようにしておきます

@jax.jit
def compute_sequential_hamiltonian_and_gradients(x, u, lambda_):
    """
    各時刻におけるハミルトニアンとその u に関する勾配を計算します。

    Parameters:
    x (jnp.array): 状態変数、形状は (N, n, 1)
    u (jnp.array): 制御入力、形状は (N, m, 1)
    lambda_ (jnp.array): ラグランジュ乗数、形状は (N, n, 1)

    Returns:
    Tuple[jnp.array, jnp.array]: ハミルトニアンの配列と勾配の配列
    """
    # ベクトル化されたハミルトニアン関数
    H = jax.vmap(hamiltonian, in_axes=(0, 0, 0))(x, u, lambda_)
    # ベクトル化された勾配関数
    hamiltonian_grad_u = jax.grad(hamiltonian, argnums=1)
    grad_u = jax.vmap(hamiltonian_grad_u, in_axes=(0, 0, 0))(x, u, lambda_)
    return H, grad_u


@jax.jit
def J_alpha(alpha, u, s):
    """argmin_{alpha} J(u + alpha * s) を算出する"""
    u_new = u + alpha * s
    u_func = diffrax.LinearInterpolation(ts=ts, ys=u_new)
    sol = diffrax.diffeqsolve(state_eq, solver, t0, t1, dt, x_0, args=u_func, saveat=saveat)
    x_new = sol.ys
    return compute_J(x_new, u_new)

最急降下法アルゴリズムの実行

%%time
from scipy.optimize import minimize_scalar

u = jnp.zeros((N, 1, 1))
eps1 = 1e-2
eps2 = 1e-7

for i in range(10**3):
    # u を与えて状態方程式の解 x を得る
    u_func = diffrax.LinearInterpolation(ts=ts, ys=u)
    sol = diffrax.diffeqsolve(state_eq, solver, t0, t1, dt, x_0, args=u_func, saveat=saveat)
    x = sol.ys

    # u, x を与えて随伴方程式の解 lambda_ を得る
    lambda_tf = S_f @ x[-1]
    x_func = diffrax.LinearInterpolation(ts=ts, ys=x[::-1])
    sol = diffrax.diffeqsolve(lambda_eq, solver, t0, t1, dt, lambda_tf, args=[x_func, u_func], saveat=saveat)
    lambda_ = sol.ys[::-1]

    H, grad_u = compute_sequential_hamiltonian_and_gradients(x, u, lambda_)

    grad_norm = jnp.sqrt(jnp.sum(grad_u**2) * dt)
    if grad_norm < eps1:
        print(f"roop done for {i=}, because {grad_norm=:.5f}")
        break

    s = -grad_u
    alpha_opt = minimize_scalar(J_alpha, bounds=(0, 1), args=(u, s)).x

    diff_norm = alpha_opt * jnp.sqrt(jnp.sum(s**2) * dt)
    if diff_norm < eps2:
        print(f"roop done for {i=}, because {diff_norm=:.8f}")
        break
    if i % 100 == 0:
        score = compute_J(x, u)
        print(f"{score=:.7f}, {grad_norm=:.5f}, {diff_norm=:.8f}")
    u += alpha_opt * s

score=28.2240219, grad_norm=14.06202, diff_norm=3.41370487
score=2.0676792, grad_norm=0.72200, diff_norm=0.00191596
score=2.0527604, grad_norm=1.48579, diff_norm=0.00058045
score=2.0234804, grad_norm=0.36918, diff_norm=0.00208106
score=2.0040922, grad_norm=0.02795, diff_norm=0.00001824
score=2.0040870, grad_norm=0.07580, diff_norm=0.00002677
score=2.0040841, grad_norm=0.05358, diff_norm=0.00003470
roop done for i=682, because grad_norm=0.00986
CPU times: user 13.7 s, sys: 0 ns, total: 13.7 s
Wall time: 13.7 s

最急降下法の計算結果

不安定平衡点の近くに状態を定める制御が構成できています

plot_control(u)

score=2.0040838718414307

共役勾配法

次のアルゴリズムで最適制御を求めます

1. 適当な $u$ を制御入力の初期推定解, $s_-=0$ とし, $d_-$ は適当（計算に使われない）に置く
2. 制御入力を $u$ としたときの状態方程式の解 $x$, 随伴方程式の解 $\lambda$ に対して $d = -\frac{\partial H}{\partial u}$ とする
3. ポラック・リビエ・ポリャック法やフレッチャー・リーブス法により $\beta$ を $d_-, d$ から定める
   • ポラック・リビエ・ポリャック法のほうが収束が速かったのでそちらを採用します
4. $s=d + \beta s_-$ とする
5. 制御入力を $u+\alpha s$と したときの評価関数値 $J[u+\alpha s]$ が最小になるスカラー $\alpha$ を求め, $u=u+\alpha s$ とおく
   • ただし, 以下の条件を満たす場合は収束したとみなす
     • 勾配のノルム $\left(\int_{0}^{T}\left\|d(t)\right\|^2\, dt\right)^{\frac{1}{2}}$ が十分小さい再場合
     • 制御の変更のノルム $\alpha \left(\int_{0}^{T}\left\|d(t)\right\|^2\, dt\right)^{\frac{1}{2}}$ が十分小さい場合
6. $d_-=d, s_-=s$ と代入する
7. 共役方向の誤差が蓄積するので定期的にリセットする（これよくわからなかったけどやらないと収束しない）

共役勾配法アルゴリズムの実行

%time
u = jnp.zeros((N, 1, 1))
s_ = jnp.zeros((N, 1, 1))
d_ = jnp.ones((N, 1, 1))

eps1 = 1e-2
eps2 = 1e-7

for i in range(10**3):
    # u を与えて状態方程式の解 x を得る
    u_func = diffrax.LinearInterpolation(ts=ts, ys=u)
    sol = diffrax.diffeqsolve(state_eq, solver, t0, t1, dt, x_0, args=u_func, saveat=saveat)
    x = sol.ys

    # u, x を与えて随伴方程式の解 lambda_ を得る
    lambda_tf = S_f @ x[-1]
    x_func = diffrax.LinearInterpolation(ts=ts, ys=x[::-1])
    sol = diffrax.diffeqsolve(lambda_eq, solver, t0, t1, dt, lambda_tf, args=[x_func, u_func], saveat=saveat)
    lambda_ = sol.ys[::-1]

    _, grad_u = compute_sequential_hamiltonian_and_gradients(x, u, lambda_)
    d = -grad_u

    grad_norm = jnp.sqrt(jnp.sum(d**2) * dt).squeeze()
    if grad_norm < eps1:
        print(f"roop done for {i=}, because {grad_norm=:.5f}")
        break

    beta = jnp.einsum("ijk, ijk", d, d - d_) / jnp.einsum("ijk, ijk", d_, d_)  # ポラック・リビエ・ポリャック法
    # beta = jnp.einsum("ijk, ijk", d, d) / jnp.einsum("ijk, ijk", d_, d_)  # フレッチャー・リーブス法
    s = d + beta * s_
    alpha_opt = minimize_scalar(J_alpha, bounds=(0, 1), args=(u, s)).x

    diff_norm = alpha_opt * jnp.sqrt(jnp.sum(s**2) * dt)
    if diff_norm < eps2:
        print(f"roop done for {i=}, because {diff_norm=:.8f}")
        break
    if i % 3 == 0:
        # s_ には共役方向の誤差が蓄積するので定期的にリセットする（？）
        s_ = jnp.zeros((N, 1, 1))
    if i % 100 == 0:
        score = compute_J(x, u)
        print(f"{score=:.7f}, {grad_norm=:.5f}, {diff_norm=:.8f}")
    u += alpha_opt * s
    d_, s_ = d, s

score=28.2240219, grad_norm=14.06202, diff_norm=3.41370487
roop done for i=71, because grad_norm=0.00364
CPU times: user 1.52 s, sys: 0 ns, total: 1.52 s
Wall time: 1.55 s

共役勾配法の計算結果

最急降下法より速く収束判定され, こちらでも制御ができています

plot_control(u)

score=2.004102945327759

わからなかったことメモ

• 終端時刻 $T=4$ を大きくすると全然収束しなくなった。。
• 勾配法に従っているのに、grad_norm や diff_norm が単調減少していない
• 共役勾配法で定期的に s をゼロに置き直す必要があるのはなぜかわからなかった